Galilean Moons-based photometry for Jupiter

• Introduction

The goal of this work is to calculate the geometric albedo of Jupiter in various photometric bands (and one non photometric). The geometric albedo is defined as the ratio between the brightness of Jupiter as observed as if it was placed at 1 Astronomical Unit (AU) from the Sun, and 1 AU from the observer, to that of a theoretical perfectly reflecting and flat surface of the same area. For this, the first result that must be obtained is the apparent magnitude of Jupiter in each desired band. The formula used to calculate the geometric albedo is taken from Mallama [1]

Photometry is usually performed using non variable stars as references. The process is complicated because it involves compensating for differences in airmass and differences in colour index. To the contrary of stars, moons are not steady sources of light, since their own magnitude is going to vary considering the solar angle, their position respective to Jupiter, and the observed longitude. But, this kind of variation can be predicted, and their effect on magnitude calculated with an acceptable precision for the ambition of this work.

• Method

The planet is imaged with the method of lucky imaging, ensuring that one galilean moon is within the same field. After a selection of good frames, they are stacked with a unnormalized arithmetic addition. Then, it is possible to calculate the magnitude of Jupiter using the moon as reference, from the equation of simple differential magnitude, example for the V band:

Vjup = vjup + (Vmoon-vmoon)

Where the lower case represents the instrumental magnitude, the upper case the transformed/catalogue magnitude.

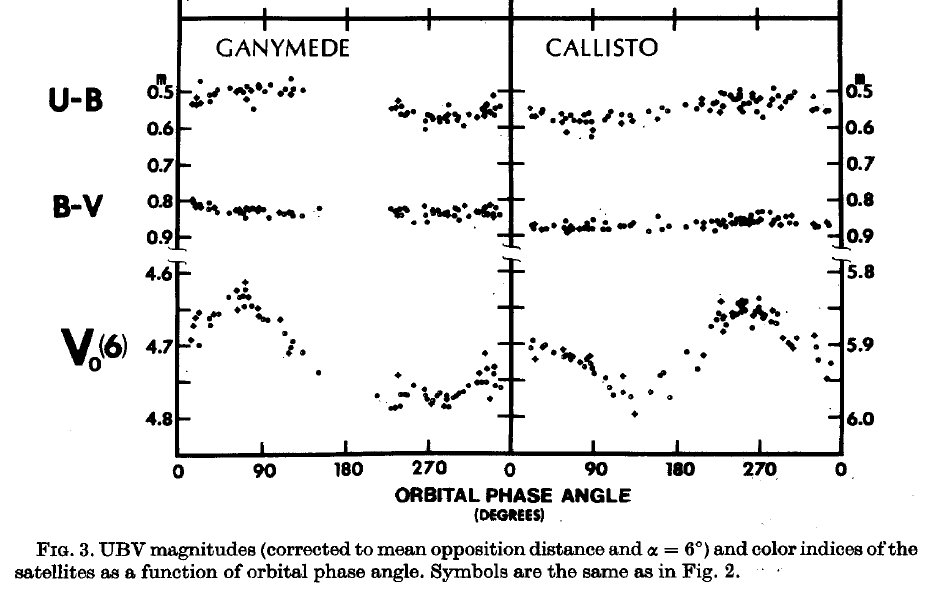
• Photometry in U, B, V bands

The apparent magnitude of the moon in the image is adjusted from an article written by R.L.Millis and D.T.Thompson in 1975 [2]. They provide first the V magnitude of each one of the moon in function of the solar angle, and for various ranges of surface longitude. This data can be compared and modified following various modern ephemeris sources, so the V magnitude of the reference moon can be reliably obtained at the moment of observation.

Then, Millis and Thompson provide the value of the B-V and U-B colour index of each moon in function of the observed surface longitude; as a result, if one has a reliable value for V, he can hope to calculate with a good precision the value of the B and U bands at the moment of the observation. The figure 1 is taken from [2]:

• Photometry in R and IR bands

Millis and Thompson do not provide data for R and IR bands, and to the knowledege of the author, no references are available in the litterature. However, one kind of data is available, which is the spectroscopic albedo of the moons. In particular, a good reference is found in two articles written by Belgacem and all [3] [4], for Europe and Ganymede, see figure 2 as example for Europe (data is from Calvin (1995)):

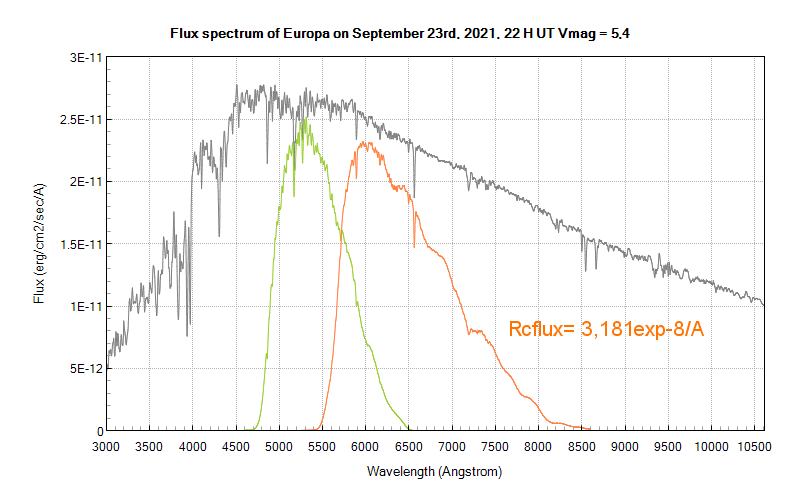
Such albedo spectra can be sent into various softwares (ISIS, Rspec) and tranformed into colour spectra, wich are obtained by multiplying them with that of a G2V star. Then, the colour spectra are transformed into flux spectra using the V magnitude of the moon at the moment of the observation.

If correctly done, flux spectra are reputed to be free from any bias and as a result, they can be used to calculate the magnitude of the object in any band, through again the equation of differential magnitude, tranforming the flux value into instrumental magnitude.

This allows to calculate the magnitude of the galilean moons in any R and IR bands, using the magnitudes of the Sun as a reference, since they are accurately known, or directly from another reliable magnitude from the moon itself – figure 3 (example):

• Results

Following Millis and Thompson, accurate/coherent B and V values have been found, but U was too high, whatever the moon used. The U value is taken from Alpy600 spectro-photometry (not described here). Following the flux method, precise values of Rc and Ic came out. z' is too low, but the author would like to discuss the reference. The albedo value for the CH4/890 band looks correct taking into account the width of the filter used (20 nm). A value for Y is proposed, that looks at least to fit the Karkokschka's spectrum from 1995. See figure 4 below.

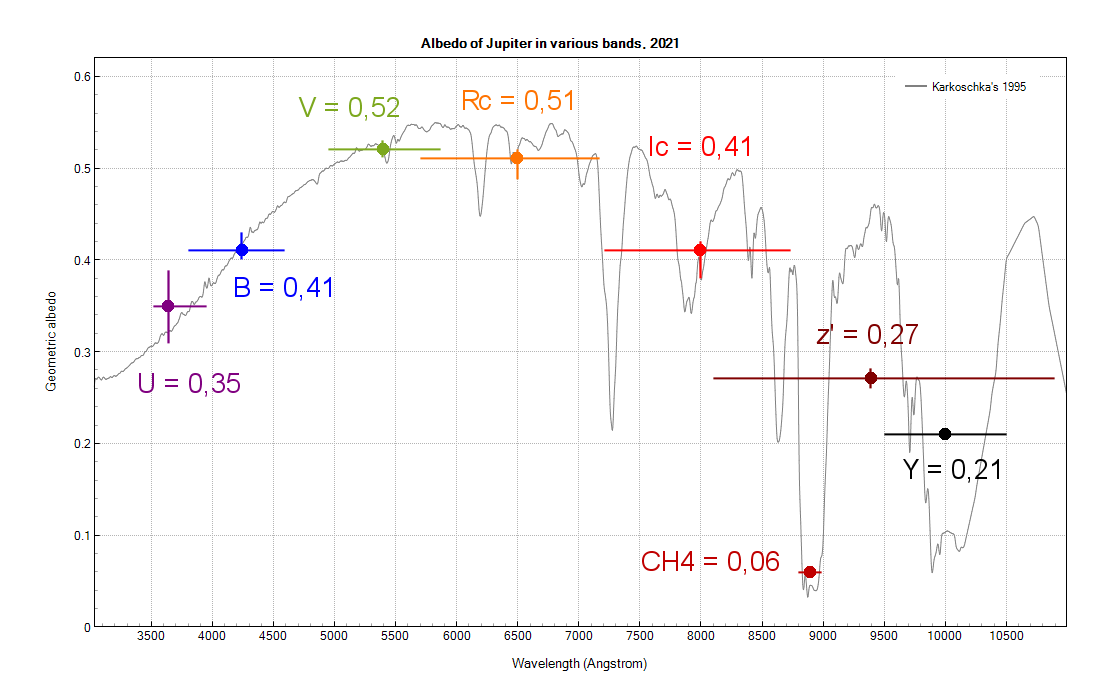
Circle: center of transmission, horizontal bar: FWHM, vertical bar is spread of the values, not the standard deviation.

• References

Web pages of the author with a wider description of the method:

http://www.astrosurf.com/pellier/galilean-photometry_UBV.html

http://www.astrosurf.com/pellier/galilean-photometry_RIC.html

http://www.astrosurf.com/pellier/galilean-photometry_discussion.html

[1] Mallama A, Krobusek B, Pavlov H (2017) “Comprehensive wide-band magnitudes and albedos for the planets, with applications to exo-planets and Planet Nine”, Icarus, Vol 282, January 2017, pages 19-33.

[2] Millis RL, Thompson DT (1975), “ UBV Photometry of the Galilean Satellites”, Icarus, Vol 26, issue 4, December 1975, pages 408-419. 

[3] Belgacem I, Schmidt F, Jonniaux G, “Regional study of Europa's photometry”, Icarus, Vol 338, March 2020, 113525. 

[4] Belgacem I, Schmidt F, Jonniaux G, “Regional study of Ganymede's photometry”, Icarus, Vol 369, November 2021, 114631.