A General Formulation of Thin-Shell Tidal Dynamics

Summary Ocean worlds like Enceladus and Europa experience tides that deform their solid shells and induce ocean currents. These worlds can be labelled thin-shell worlds; their outermost layers (ocean and ice shell) are thin compared to the radius. We present a new model to study the tidal response of thin-shell worlds. Compared to previous work, our model can accommodate radial density stratification of the ocean and lateral variations of layer properties such as thickness. We examine how these factors affect the tidal response. Ocean thickness variations change the characteristic eigenfrequencies of thin-shell worlds and alter the eigenmodes excited by the tidal force. Zonal thickness variations hinder Rossby waves excited by the obliquity tide and we argue this has important implications for the thermal and orbital evolution of Triton and the Moon. Internal gravity modes are excited in stratified subsurface oceans. Energy dissipation due to resonant internal gravity waves can contribute to the thermal budget of some moons, especially small icy worlds like Enceladus where energy dissipation due to internal tides is compatible with the observed endogenic activity. 

1. Introduction 

Tides play an essential role in the thermal and orbital evolution of planets and moons.  A clear example are icy moons with subsurface oceans. Tides deform and might crack their ice shells, drive ocean currents, and result in energy dissipation that can dominate the body's internal heat budget.   

Many icy moons can be described as thin-shell words. Their outermost layers consist of a liquid shell covered by a solid shell, both of which have a small thickness compared to the radius. Bodies with shallow magma oceans also fall within this category. The dynamics of these bodies can be described by vertically averaging the mass and momentum conservation equations, leading to the Laplace Tidal Equations for the ocean (Laplace, 1798) and the viscoelastic thin-shell equations for the solid shell (e.g., Beuthe, 2018).

Thin-shell dynamics have been used to describe the tidal dynamics of subsurface oceans and ice shells of icy moons (e.g., Tyler, 2008; Matsuyama et al., 2018; Beuthe,2016, 2018). Previous work has often relied on the assumptions of (1) no density stratification and (2) no lateral properties variations (e.g., ocean thickness). However, both (1) and (2) can be relevant in thin-shell worlds. Geographical variations in tidal heating can cause lateral variations in shell thickness (Ojakangas & Stevenson, 1989). Gravity and altimetry data indicates that Enceladus' ocean and ice shell vary in thickness (Beuthe et al., 2016; Hemingway & Mittal, 2019; Câdek et al., 2016); and recent work shows that different processes can produce and maintain stratified density profiles.   

We develop a spectral method based on spherical harmonics that allows to efficiently compute the tidal dynamics of thin-shell worlds and apply it to several cases where assumptions (1) and (2) are not justified. 

2. Unstratified Shells of Constant Thickness

The tidal response of unstratified oceans of constant thickness covered by constant thickness shells has been widely studied (e.g., Beuthe et al., 2016; Matsuyama et al., 2018). The ocean response to the eccentricity and obliquity tide is given by a combination of surface gravity and Rossby modes whose eigenfrequencies depend on the Lamb parameter (Ω²R²/gH_ocean) and the effective rigidity (EH_lid/gρR²). These modes can resonate with the tidal force and result in strong ocean currents and subsequent energy dissipation.

Surface gravity modes are resonant for ocean thicknesses much smaller than those characteristic of the moons of the outer Solar System. The obliquity tide can excite Rossby waves of high amplitude, which can become an important contributor to the thermal budget in moons with high orbital obliquity like Triton. 

3. Unstratified Shells of Variable Thickness

Ocean thickness variations alter the eigenfrequencies of the system and can introduce new resonant modes. Equatorially asymmetric thickness variations allows the excitation of asymmetric modes by the symmetric eccentricity tide and symmetric modes by the asymmetric obliquity tide. While oceans of uniform thickness always respond with a longitudinal wave length equal to that of the tidal forcing, the tides of oceans with sectorial and tesseral thickness variations contains different longitudinal wave lengths. 

Energy dissipation due to Rossby waves excited by the obliquity tide is severely reduced when zonal ocean thickness variations are considered. We show that even a small deviation from uniform thickness can lead to a decrease of energy dissipation of orders of magnitude. We argue that this allows to reconcile a primordial origin of the Moon's obliquity with the presence of a long-lived magma ocean early during its evolution.

4. Stratified Shells of Constant Thickness 

Ocean stratification makes it possible for the tidal force to excite internal gravity modes that propagate at the interface between layers of different density. 

We consider a simple two-layer ocean to study internal gravity waves and show that internal modes can be specially relevant in moons with high effective rigidity. This is the case of Enceladus for which we find that resonant internal waves in stratified oceans with Δρ/ρ>10^-3 can lead to tenths of GW of energy dissipation. Internal modes are characterised by a strong shear at the density interface that can lead to Kelvin-Helmholtz instabilities, ocean mixing and hence feedback to the ocean stratification structure. 

 

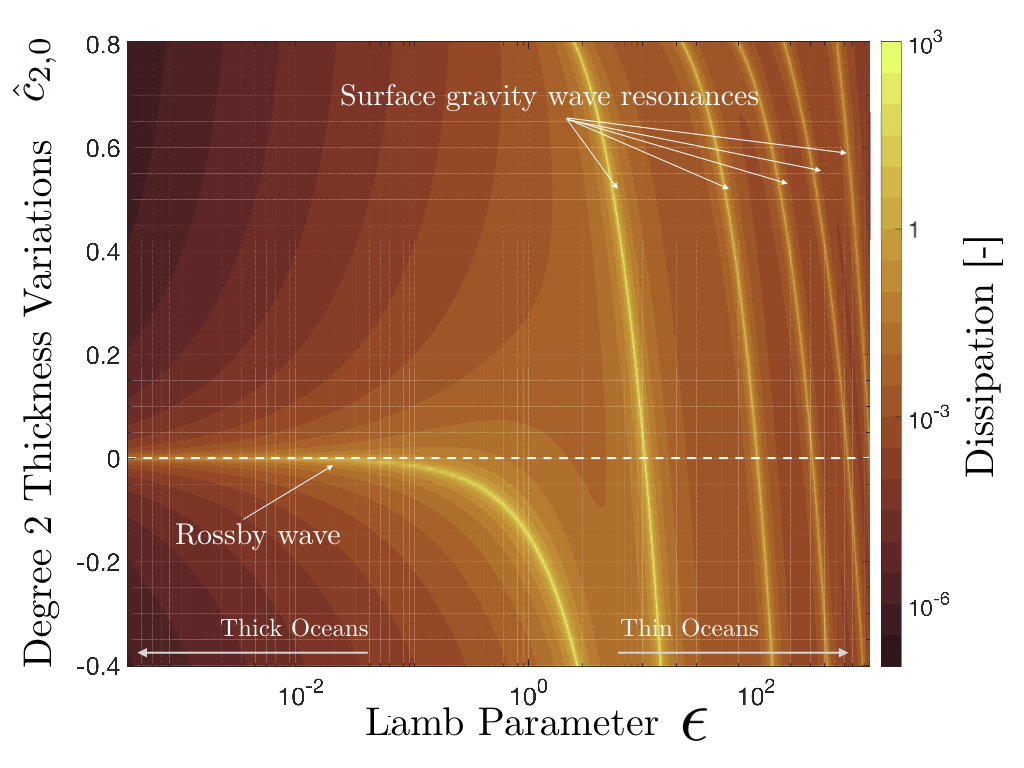
Figure 1: Energy dissipation due to obliquity tides in a surface unstratified ocean with degree two ocean thickness variations. 

 

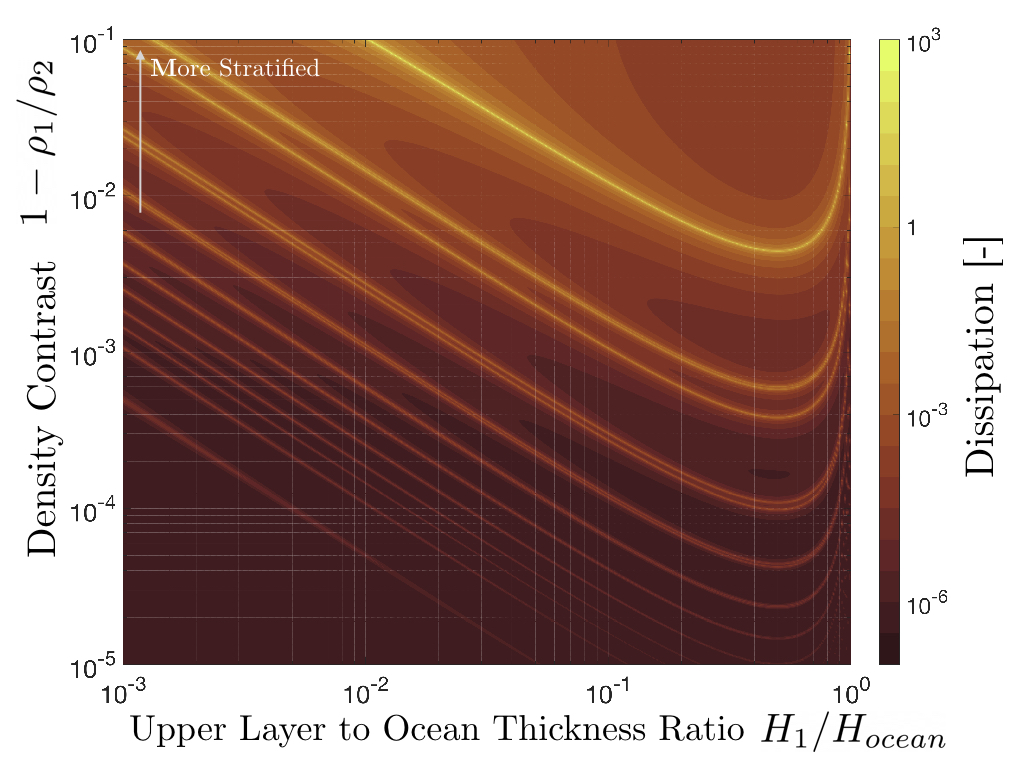
Figure 2: Energy dissipation due to internal waves excited by the eccentricity tide in a stratified subsurface ocean with Lamb parameter 5·10^-3 and effective rigidity 10 (similar to Enceladus).

References

Beuthe, M. 2016, Icarus, 280, 278 , doi: 10.1016/j.icarus.2016.08.009

—. 2018, Icarus, 302, 145, doi: 10.1016/j.icarus.2017.11.009

Beuthe, M., Rivoldini, A., & Trinh, A. 2016, Geophys. Res. Lett., 43,10,088, doi: 10.1002/2016GL070650

Câdek, O., Tobie, G., Van Hoolst, T., et al. 2016, Geophys. Res. Lett., 43, 5653, doi: 10.1002/2016GL068634

Hemingway, D. J., & Mittal, T. 2019, Icarus, 332, 111 , doi: 10.1016/j.icarus.2019.03.011

Laplace, P.-S. 1798, Traité de mécanique céleste, Tome II, Livre IV, Des oscillations de la mer et de l’atmosphère

Matsuyama, I., Beuthe, M., Hay, H. C., Nimmo, F., & Kamata, S. 2018, Icarus, 312, 208 , doi: 10.1016/j.icarus.2018.04.013

Ojakangas, G. W., & Stevenson, D. J. 1989, Icarus, 81, 220 , doi: 10.1016/0019-1035(89)90052-3

Tyler, R. H. 2008, Nature, 456, 770, doi: 10.1038/nature07571