Artificial Neural Network classification of asteroids in the M1:2 mean-motion resonance with Mars.

1. Introduction

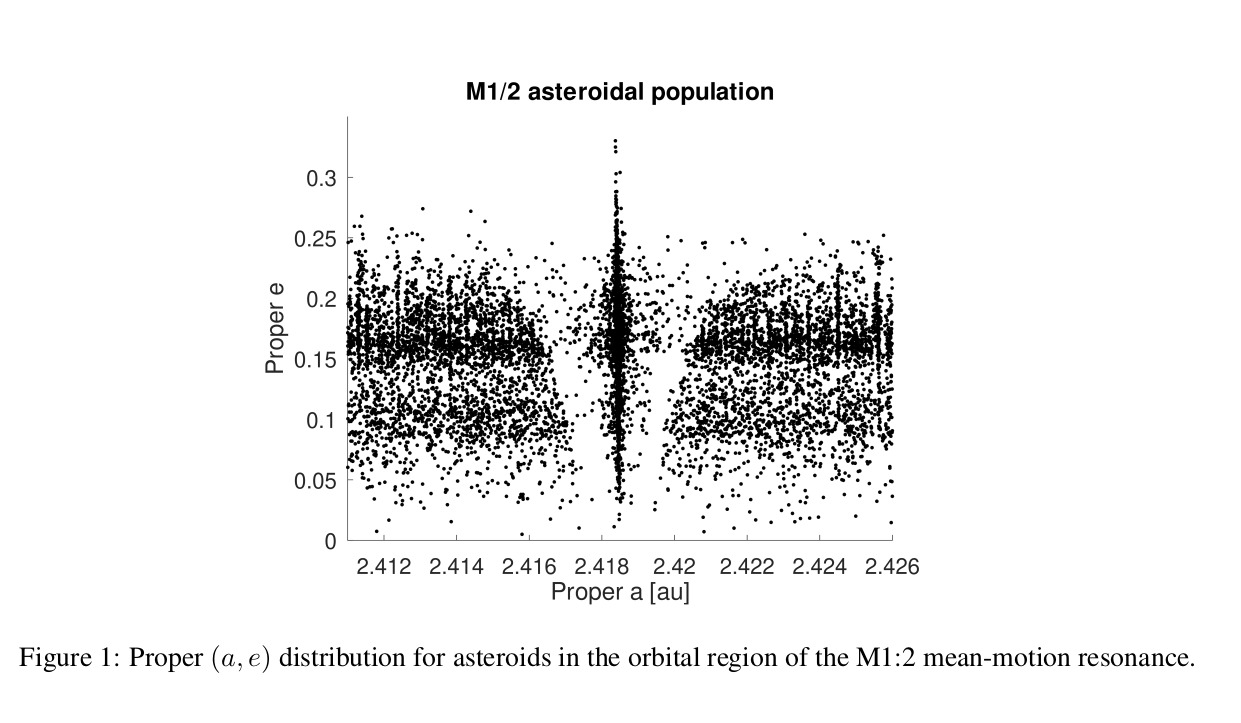
During the last five years, machine learning and deep learning have been used more commonly in the field of asteroid dynamics. Artificial neural networks have been recently used for identifying members of asteroid families [6]. This is the first attempt to use deep learning for the automatic classification of images of asteroids resonant arguments. The population of asteroids inside the M1:2 mean motion resonance with Mars was studied by [4]. The V-shaped region at the resonance center in the proper (a, e) plane (see figure (1)) is associated with the M1:2 resonance. [4] defines two main resonant arguments. σ is given by:

where λ = M + Ω + ω is the mean longitude, ϖ = Ω + ω, with Ω the longitude of the node, ω the argument of pericenter, and where the suffix M identifies the planet Mars. σ₁ is defined as:

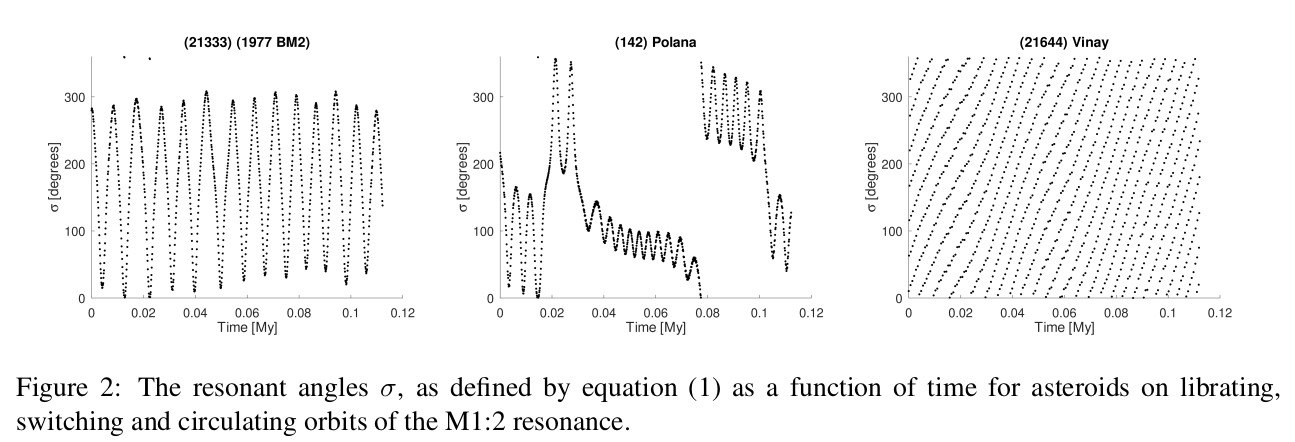
The orbital behavior of asteroids in the affected region can be identified by studying the time dependence of these two angles. Asteroids for which the critical arguments cover the whole range of values, from 0◦ to 360◦, are on circulating orbits. If the argument oscillates around an equilibrium point, we have a librating orbit. Whether the argument alternates phases of libration and circulations we have a switching orbit, as defined in this work. The main equilibrium point for the σ₁ argument is near 0◦. Pure σ librators tend to be much rarer than pure σ₁ ones. Since in this work we are interested in treating a multi-class problem we focus our study on the case of the σ₁ resonant argument.

2. Artificial Neural Networks (ANN)

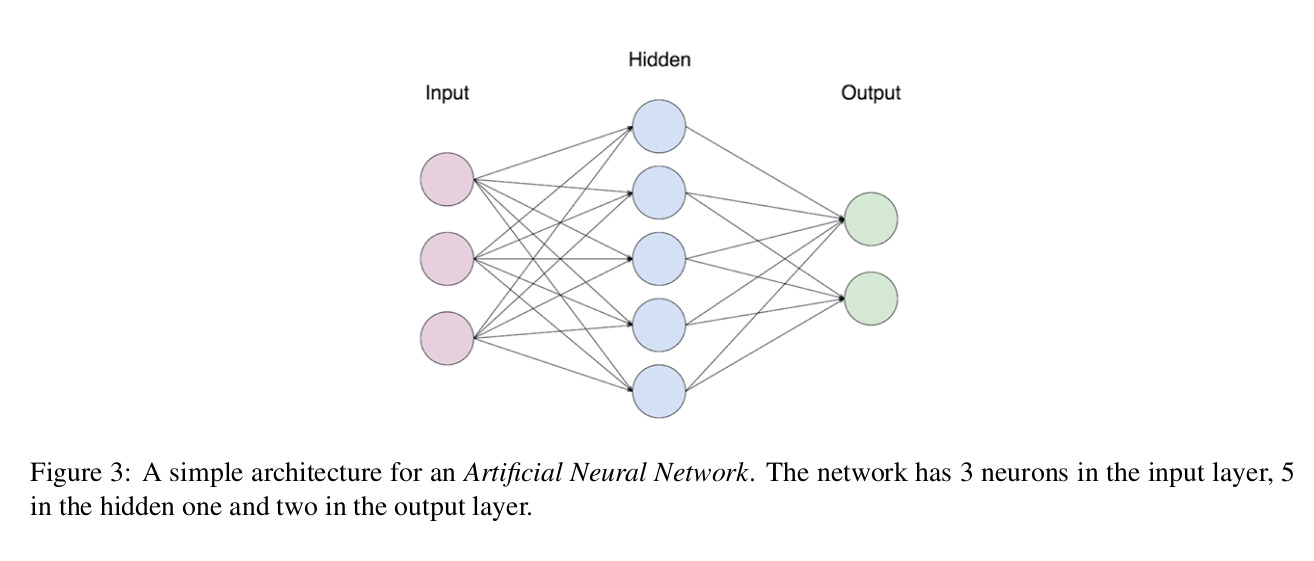
Artificial neuron networks mimic the neuron's web in a biological brain. Each artificial neuron can transmit a signal to other neurons. This signal can be processed, and the signal coming out of each neuron is computed as a non-linear function of the inputs. A basic architecture for ANN consists of an input and an output layers, with the possible presence of one or more hidden layers between them to improve the model precision. Each neuron will perform a weighted sum, W_S, given by:

where n is the number of input to process, X_i are the signals from other neurons, and w_i are the weights.  ANN will optimize the values of the weights during the learning process. On the weighted sum W_S, ANN will apply an activation function. For images classifications, one of the most used activation function is the “relu”, defined as:

which will produce as an outcome the weighted sum itself W_S, if that is a positive number, or 0, if W_S has a negative value. As a next step, the loss function must be applied to all the weights in the network through a back-propagation algorithm. A loss function is usually calculated by computing the differences between the predicted and real output values. Interested readers can find more information in the Keras documentation (https://keras.io/, [5]).

3 Applications of ANN to M1:2

Here, we used the Keras implementation of ANN, which is based on the Tensorflow Python software package [2]. The process used in this work is the following:

1. The asteroid orbits are integrated under the gravitational influences of the planets.
2. We compute the resonant arguments.
3. Images of the time dependence of resonant arguments are drawn.
4. The ANN trains on the training label image data.
5. Predictions on the test images are obtained, and images of the test data, with their classification, are produced.

To identify resonant argument images, we created a four-layer model with a flatten, an inner, a hidden, and an output layers. The flatten layer will transform the image matrices into arrays. The inner layer will look for simpler patterns in the arguments images, while the hidden layer will search for more complex features. The output layer, with three nodes, will perform the final classification for the three possible classes.  To quantitatively classify the outcome of ANN, it is often useful to compute values of metrics. [3] defines accuracy as:

Our model performs quite well: Accuracy values were all above 0.996.

4. ML identification of resonant groups

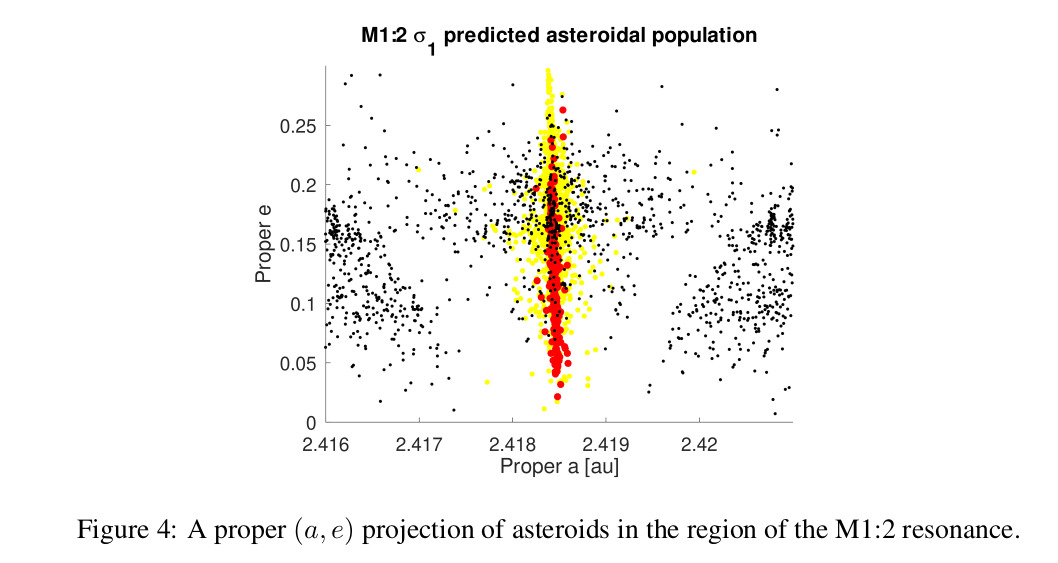
Using ANN and ML, we obtained labels for 6440 asteroids in the M1:2 resonance region. We then used the ML Hierarchical Clustering Method (ML-HCM) of [1] to identify asteroid groups among the resonant population of M1:2 resonators. Our analysis produced seven possible groups, all associated with the Massalia, Nysa, and Vesta families. This confirms the analysis of [4].

5. Summary and Conclusions

The use of ANN allowed us to classify the orbital type of all numbered asteroids affected by the M1:2 resonance. The identification of clusters in the population of asteroids in librating and switching orbits suggested that three asteroid families, those of Massalia, Nysa, and Vesta, are the most dynamically affected by this resonance.

Acknowledgements

We would like to thank the Brazilian National Research Council (CNPq, grant 301577/2017-0). More information on this work can be obtained from Carruba et al. (2021), MNRAS, 504, 692.

References
[1] CARRUBA, V., ALJBAAE, S.,  AND  LUCCHINI, A. Machine-learning identification of asteroid groups. MNRAS 488, 1 (Sept. 2019), 1377–1386.
[2] CHOLLET, F., AND OTHERS. Keras: The Python Deep Learning library, (June 2018).
[3] FAWCETT, T. An introduction to ROC analysis. Pattern Recognition Letters 27, 8 (Jun. 2006), 861 –874.
[4] GALLARDO, T., VENTURINI, J., ROIG, F., AND GIL-HUTTON, R. Origin and sustainability of the population of asteroids captured in the exterior resonance 1:2 with Mars. Icarus 214, 2 (Aug. 2011), 632–644.
[5] LECUN, Y., BENGIO, Y., AND HINTON, G. Deep learning. Nature 521, 7553 (May 2015), 436–444.
[6] VUJIČIĆ, D., PAVLOVIĆ, D., D., M., Ð ORÐEVIĆ, S., S., R., AND D., S. Classification of asteroid families with artificial neural networks. Serb. Astron. J. 200 (Dec. 2020), 1–8.