Gravity Traverse Simulations for Small Bodies and Moons of the Solar System using the Wedge-Pentahedra Method

Introduction

Rovers, both crewed and robotic have a long tradition in Solar System exploration. Most notably, Lunar and Martian exploration made use of vehicles to explore the surface, including three lunar roving vehicles carrying Apollo astronauts and equipment [1]. More recently, small body (SB) exploration missions started to have landers with mobility included in their mission architectures. The MINERVA-II rovers were part of the Hayabusa2 mission [2] and the two successful rovers became the first rovers on an asteroid, followed by the MASCOT rover [3]. All these probes are referred to as “rovers” as they moved around the surface, irrespective of the movement being realized by hopping, rather than driving. Regarding the latter, the Martian Moon eXplorer (MMX) mission will include a rover with “classical” wheeled locomotion to explore the Phobian surface [4]. Such missions demand careful surface traverse planning, and detailed gravity simulations, taking into account the local topography, being beneficial for both rover operations and the mission’s science return. A prime example for a science application is the use of a surface gravimeter, such as the Apollo 17 TGE [5], or the GRASS gravimeter under development for the ESA Hera mission [6, 7]. This work presents a traverse simulator for local locomotion, accounting for local topography when computing the resulting surface gravity.

Methodology

The Traverse And Gravity Simulator (TAGS) is built upon the Wedge-Pentahedra Method (WPM) [8]. This method allows precise, high-resolution surface representation, and the assessment of the local terrain’s influence on the (surface) gravitation (topographic correction). In continuation of previous work [8], the evaluation location in the TAGS is varied to represent a surface (rover) traverse. The 3D-orientation of the gravitation vector is computed, and hence the variation of the vector orientation with respect to the initial reference gravitation along the traverse is plotted in the simulator. Likewise, the resulting gravity g_res and the “vertical” component g_z along the rover traverse is plotted, illustrating the variations over the non-spherical body’s surface, and due to the local (artificial) topography. Variation of the terrain scale factor S_T further allows to compare the influences of terrain with variable amplification, where larger scale factors are representative of larger terrain amplitudes, e.g. higher hillocks and deeper craters. While the WPM is only concerned with gravitation, the TAGS is purposely referring to gravity, as the simulator will allow to include additional (dynamical) effects to the resulting gravity, such as the contributions form rotation, libration and tides.

Applications

To show the TAGS working and illustrate the local surface gravity variations, a rover traverse on the Martian moon Phobos has been simulated. Starting in the centre of the terrain, the traverse step between the individual evaluation points are +50 m in +X-direction, and −50 m in –Y-direction for both routes. TAGS simulation results for a total of twelve gravity evaluation stations is plotted in Figures 1 and 2 for which two different terrain scale factors (amplification of local topography) S_T = 100 and S_T = 500 are used.

 

 

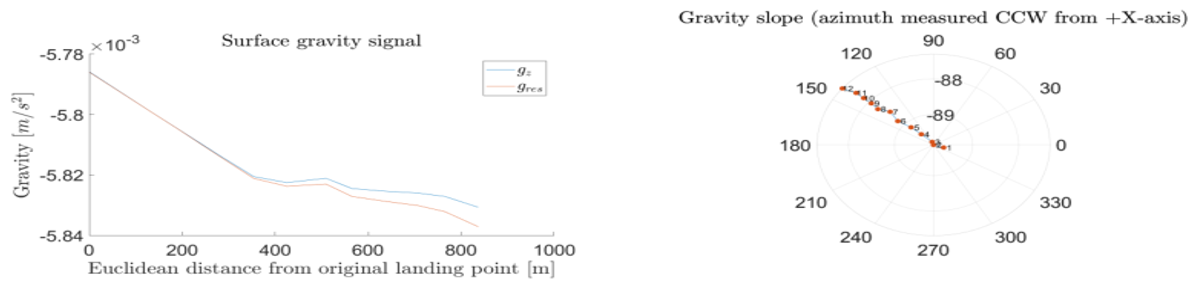
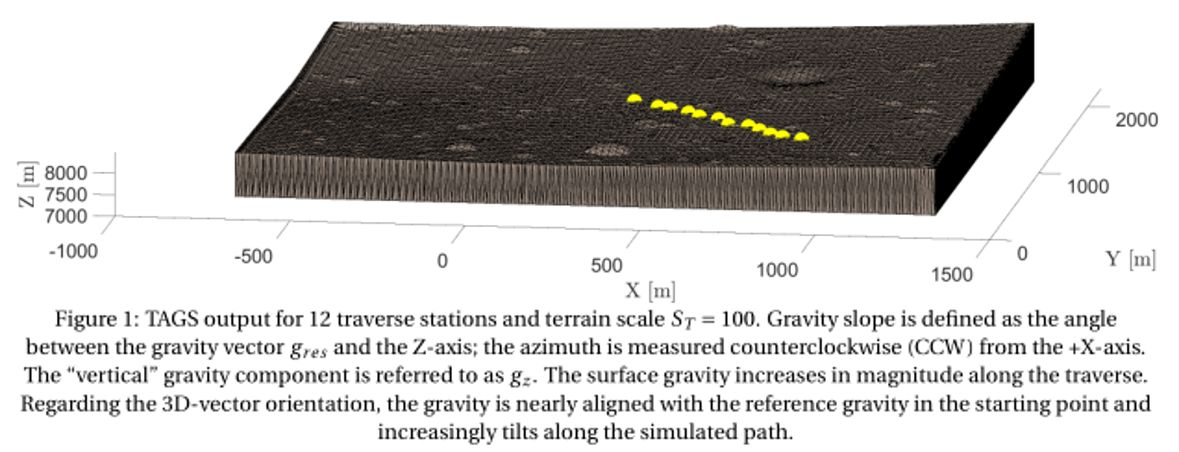
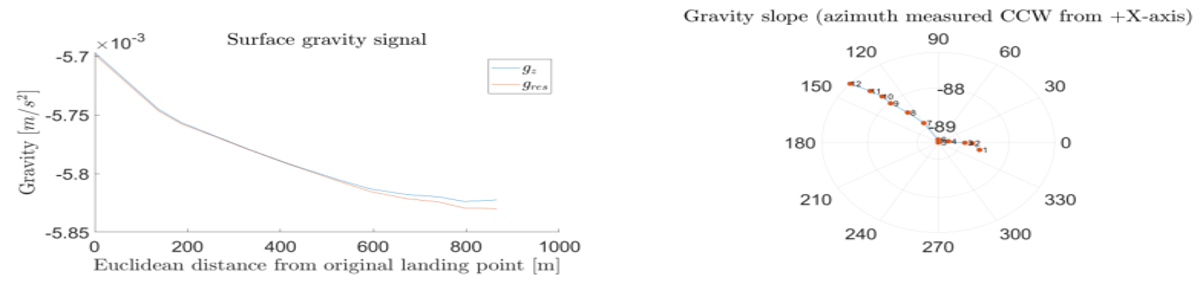
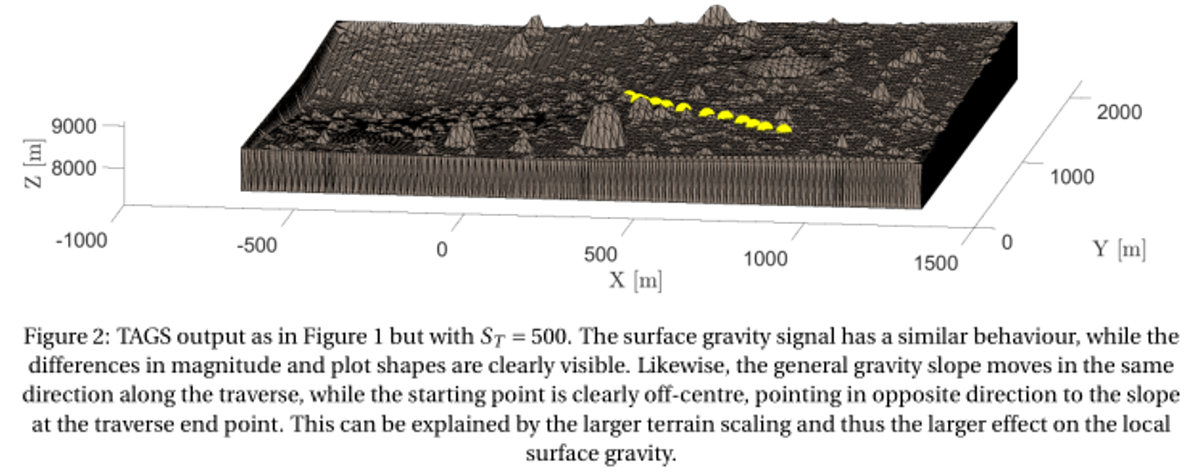
Regarding the surface gravity signal in the two compared rover traverses, the overall gravity signal is similar in both magnitude and increasing trend along the traverse. However, the TAGS simulation likewise clearly illustrates the gravity differences experienced in both traverses, due to the local topographical differences. For S_T = 100, the resulting gravity g_res ranges from (5.786 – 5.837) ×10^-3 m/s², whereas for S_T = 500, g_res is ranging from (5.698 – 5.830) ×10^-3 m/s². The larger terrain scaling (S_T = 500) results in a gravity 1.521 % and 0.120 % smaller compared to the “flatter” terrain (S_T = 100), for the lower and upper limit, respectively. In addition, it can be well observed that the “vertical” Z-component of the gravity g_z diverges from g_res, caused by increasing gravity vector inclinations with respect to the reference g_ref, likewise well observable in the TAGS polar plots (2.7° for S_T = 100; 2.9° for S_T=500).

Outlook

We will quantify the local terrain’s influence on the surface gravity along the traverse, which has implications both on surface sciences (e.g. gravimetry) and landing/surface operations. This is specifically important, as the WPM considers high-resolution digital elevation models on a local scale with a ground resolution much better than the global shape file resolution of the target (small) body. The here presented Traverse And Gravity Simulator (TAGS) allows for detailed traverse planning of exploratory rovers on extraterrestrial surfaces, both using artificial and newly obtained (real) local terrain data. TAGS can be extended in its applications, e.g. by integrating dynamical contributions to gravity, simulating illumination conditions, or for public outreach and education.

Acknowledgements

M.N. acknowledges funding from the Foundation of German Business (sdw) and the Royal Observatory of Belgium (ROB) PhD grants. The authors acknowledge funding from BELSPO via the PRODEX Programme of ESA and from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 870377 NEO-MAPP.

References

[1] Asnani, Vivake, et al. “The development of wheels for the Lunar Roving Vehicle.” Journal of Terramechanics 46.3 (2009): 89-103.

[2] Van Wal, Stefaan, et al. “Prearrival deployment analysis of rovers on Hayabusa2 asteroid explorer.” Journal of Spacecraft and Rockets 55.4 (2018): 797-817.

[3] Ulamec, Stephan, et al. “Landing on small bodies: From the Rosetta Lander to MASCOT and beyond.” Acta Astronautica 93 (2014): 460-466.

[4] Michel, Patrick/Ulamec, Stephan, et al. “The MMX rover: performing in situ surface investigations on Phobos.” Earth, Planets and Space 74.1 (2022): 1-14.

[5] Talwani, M., et al. “13. Traverse Gravimeter Experiment” Apollo 17: Preliminary Science Report (1973): 13-1 – 13-13.

[6] Karatekin, Özgür, et al. “Surface gravimetry on Dimorphos.” EGU General Assembly Conference Abstracts. 2021.

[7] Noeker, Matthias, et al. “The GRASS Gravimeter Rotation Mechanism for ESA Hera Mission On-Board Juventas Deep Space CubeSat.” Proceedings of the 46^th Aerospace Mechanisms Symposium, Virtual, May 11-13, (2022): 159-172.

[8] Noeker, Matthias, et al. “Artificial terrain on Phobos: Assessing the influence on local gravity using the Wedge-Pentahedra Method” No. EPSC2021-370. Copernicus Meetings, 2021.