New approach to planetesimal formation: clusters of heavy particles in two-dimensional Keplerian turbulence

Introduction

Planetary systems form from sub-micron sized dust embedded in a mostly gaseous protoplanetary disk. Dust has to grow into planetesimals (∼ km sized objects) considered to be the building blocks of planets. We see reminiscences of these objects in the solar system small bodies, such as asteroids and comets, that have been left over from the planets genesis process. However, planetesimal formation is still one of the major open questions in planet formation theory. Solids can’t grow up to asteroid size relying only on sticking after pairwise collisions, due to the fragmentation barrier and the drift barrier [1]. The favoured solution is to form dense particle clumps, with low velocity-dispersion, that can then collapse under self-gravity. However the way in which the solids can be concentrated, e.g. streaming instability [2] or Rossby wave instability [3], is highly debated and can be modelled as a turbulent dynamic in the disk. To understand planetesimal formation it is then fundamental to study jointly the turbulent dynamics. In this context, we model the dynamics of particles in turbulent flows with Keplerian rotation and shear. To address this astrophysical problem we use fluid-dynamics methods to provide innovative perspectives on this challenging question.

Method

We model the dynamical evolution of the protoplanetary disk’s dust coupled to the gas phase. We perform 2D direct numerical simulations using a pseudo-spectral solver and the shearing box approach, in which the incompressible Navier-Stokes equation is solved locally with shear periodic boundary conditions. The gas is maintained turbulent through an external stochastic forcing. We use an Eulerian approach for the fluid while we implement the dust as Lagrangian particles. We explore various values of the rotation frequency Ω and the solid response time τ , a parameter related to the particle size. We analyse the results using tools borrowed from the study of dynamical systems.

Fractal and strong clustering of solids

In order to characterize the dust dynamics in the flow and to identify in which case there is a strong concentration of the solids that could lead to small body formation, the Lyapunov dimension dL is calculated for each run (Fig. 1a). This quantity gives an estimation of the fractal attractor dimension in the phase space [4]. We find three different regimes. At low rotation rate and for large particle size we obtain dL > 2, therefore the inertial particles fill the whole space. Focusing instead on intermediate values of the response time, for small rotation rates the particles are expelled from the eddies and form fractal structures (Fig. 1b), while they tend to concentrate inside the anticyclones for larger Ω (Fig. 1c). Particles eventually form a pointwise cluster for dL = 0 (Fig. 1d).

We then inspected the mass distribution of solids in the domain. Analysing a case that falls into the strong clustering regime (Ω=64/3, τ=0.05) we find that the different clusters of particles tend to merge with time to form a unique pointwise cluster at the end of the simulation (Fig. 2a). In order to estimate the interaction strength between sets of n particles, we then calculated the fractal dimensions Dn for different values of the rotation frequency and the solid response time (Fig. 2b, Fig. 2c). This dimensions characterize the anomalous scaling typical of multifractal attractors [5]. We notice that for the strong clustering case (Fig.2b, Ω=64/3) the attractor is homogenous with its fractal dimension Dn = 0 for all n. We instead find that when particles cluster fractally the attractors are multifractals that show decreasing values of Dn with increasing n. This behaviour at large n is particularly interesting for the gravitational collapse of dust: it means that particles in numerous groups will interact strongly, therefore possibly collapsing under self-gravity to form a planetesimal.

Conclusions and future perspectives

We have identified promising tools for the understanding of planetesimal formation. We also showed how the behaviour of dust particles in a turbulent flow drastically change with increasing rotation rate, leading to the formation of strong dust clumps. In the future the back-reaction from dust on gas will be added, particularly important for triggering the streaming instability. Self-interaction between solids particles (e.g. collisions, gravity) will also be considered to study how dust in vortices can accrete and form large aggregates.

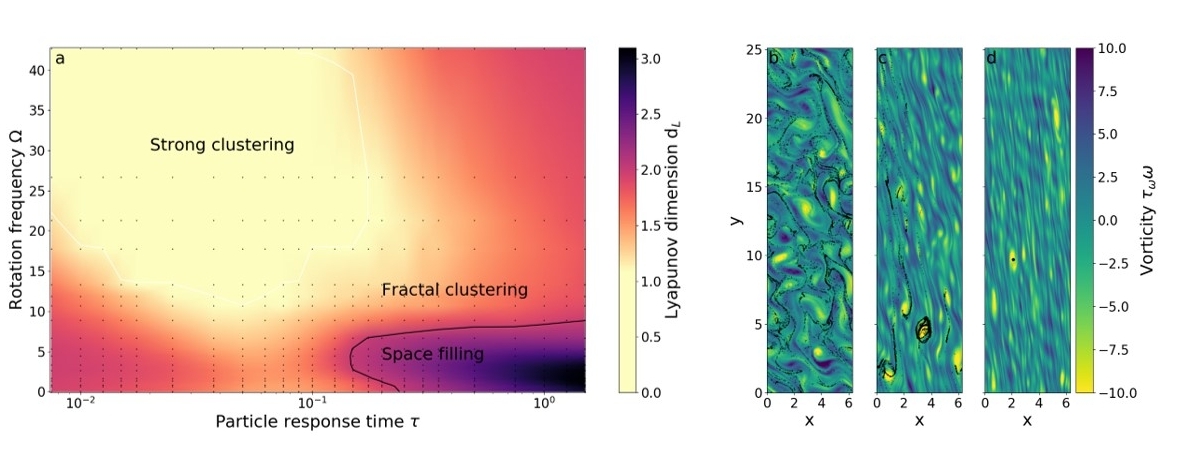
Figure 1: a) Phase diagram of the rotation frequency Ω vs the particle response time τ . The colour-code is for the Lyapunov dimension dL. b) Snapshot of dust particles position and fluid vorticity at t=200 for Ω=4/3 and τ=0.1 c) for Ω=32/3 and τ=0.1. d) for Ω=80/3 and τ=0.1.

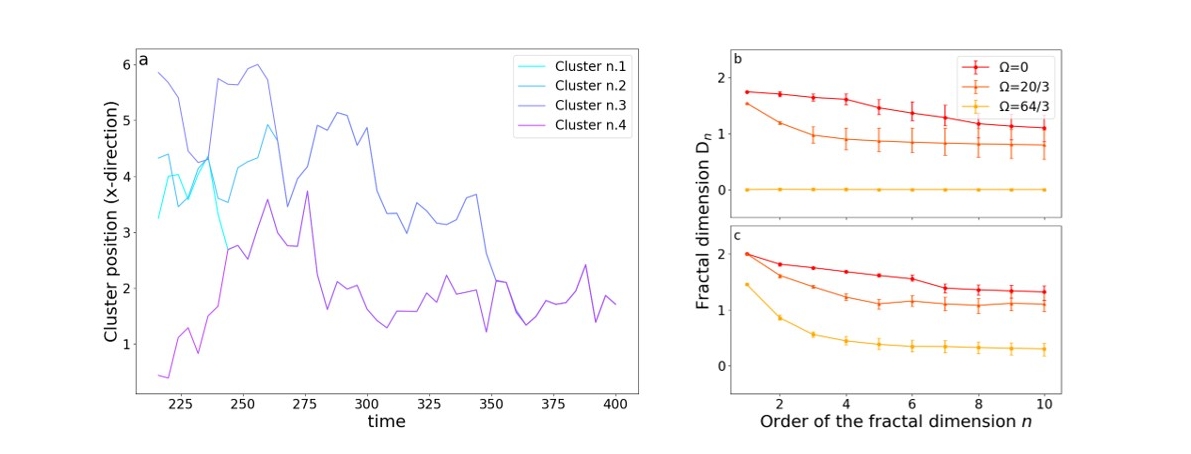
Figure 2: a) Path of different clusters of particles along time for Ω=64/3 and τ=0.05. b) Fractal dimension Dn as a function of the order of the fractal dimension n for different  values of rotation frequency Ω and τ=0.025 c) and τ=0.5.

Bibliography

[1] L. Testi, T. Birnstiel et al., Dust Evolution in Protoplanetary Disks, Protostars and Planets, IV, 339-361 (2014).
[2] A. N. Youdin and J. Goodman, Streaming Instabilities in Protoplanetary Disks, The Astrophysical Journal, 620, 459–469 (2005).
[3] R. V. E. Lovelace, S. A. Colgate, A. F. Nelson, Rossby Wave Instability of Keplerian Accretion Disks, The Astrophysical Journal, 513, 805-810 (1999).
[4] J.L. Kaplan and J.A. Yorke, Chaotic behavior of multidimensional difference equations, Proceedings on Functional Differential Equations and Approximation of Fixed Points, 730, 204-227 (1979).
[5] G. Paladin and A. Vulpiani, Anomalous scaling laws in multifractal objects, Physics Reports, 156, 147-225 (1987).