SB4

The activity evolution of comets along their orbits around the Sun has not yet been fully understood. Especially around perihelion, comets show an abnormally high dust and water activity, growing far more rapidly than the increase in energy from the incoming sunlight (e.g. Skorov et al., 2020; Combi et al., 2020). To better understand this complex phenomenon, we developed a thermophysical model that encompasses mass-transfer of volatile species and the resulting build-up of pressure. We based our model on the assumption of a comet nucleus that was formed by gravitational collapse of dust-ice pebbles (Blum et al., 2017).

With these conditions in mind, this model was designed for numerically solving the one-dimensional heat transfer equation (HTE) for porous media. It solves the HTE through an explicit finite-difference scheme to more easily incorporate the temperature-dependent thermal conductivity. The thermal conductivity for a pebble system was implemented in accordance with Gundlach and Blum, 2012. The model calculates sublimating and resublimating particles via the Hertz-Knudsen equation and uses the resulting values to calculate the latent heat transfer. Sub-surface gas pressure levels become available for analysis through this microphysical approach. For ice-dust layers, we calculate the reduced gas flux through dust layers via a reduction function, as used in Gundlach, Fulle and Blum, 2020. Furthermore, dust ejection through pressure build-up for ultra-low tensile strength layers is an included effect, which can be used for calculating the ejected dust mass of a comet.

The current model is designed for applications with dust-ice pebbles, where H₂O and CO₂ are the main volatile species, but the implementation is adaptable for different scenarios and allows applications for non-porous media and addition of multiple volatile species. 

Figure 1: An example of the resulting temperature profile of our model. It shows the temperature and the volatile species content of the layers as a function of depth for a simulation of comet 67P/Churyumov-Gerasimenko close to perihelion. The two dotted lines mark the current position of the sublimation fronts of the volatile species.

Figure 2: An example of an ejection event of the top three layers during a simulation of comet 67P. The first plot shows the temperature profile and volatile species content on the time step before the ejection occurred, the second plot shows these parameters immediately after the ejection occurred

Figure 1 shows the effect of the latent-heat transfer on the temperature profile. The profile shows a  dent at the diurnal skin depth and another dent where the sublimation front of the water ice is located. Figure 2 shows the effect of a dust-ejection event on the temperature profile. We will discuss these effects on the temperature profile as well as different applications of the model. Furthermore, we will discuss the way our model includes the microphysical properties of the pebbles and the latent-heat transfer numerically. 

References:

Skorov Y. et al., 2020, MNRAS 494.3, pp. 3310-3316.

Combi M. R. et al., 2020, The Planetary Science Journal 1.3, p. 72.

Blum J. et al., 2017, MNRAS 469, pp. 755-773.

Gundlach B. and Blum J., 2012, Icarus 219.2, pp. 618-629.

Gundlach B., Fulle M. and Blum J., 2020, MNRAS 493.3, pp. 3690-3715.

How to cite: Schuckart, C., Bischoff, D., Gundlach, B., Bürger, J., Attree, N., and Blum, J.: Thermophysical modelling of comets: one dimensional microphysical modelling of cometary activity, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-148, https://doi.org/10.5194/epsc2022-148, 2022.

Introduction

After the visit of comet 1P/Halley by the Giotto mission, “KOSI” (comet simulation) – the first large scale laboratory campaign for cometary research – investigated various physical phenomena occurring on comets by using analogue materials. The experiments were also accompanied by intensive modeling activity, which yielded several thermophysical models for the description of comets [1]. Following the revolutionary findings of the Rosetta mission, however, a new laboratory campaign became necessary to adapt existing models and to incorporate the new knowledge acquired. Thus, the “CoPhyLab – Comet Physics Laboratory” project was initiated in 2018 by an international consortium (www.cophylab.space).

In the framework of this project so far, we have used several individual experiments to characterize various materials as potential ingredients for a new cometary analogue. In parallel, the construction of a large cryogenic vacuum chamber (“L-Chamber”) was completed, enabling the measurement of refractory-volatile mixtures by multiple instruments simultaneously. While cometary activity involves various physical processes, such as sublimation and gas diffusion in porous materials, understanding the comet’s thermal behavior is crucial. A rigorous thermophysical model (TPM) that considers the porous structure of the cometary material, as well as the volatile phases, and processes connected to them (sublimation, phase changes etc.), would significantly improve the understanding of the evolution of comets.

Here, we present a strategy for the development of a new TPM that in the first phase is able to describe the laboratory experiments and ultimately can be scaled to cometary environments to assist the interpretation of data collected by observations and space missions.

Strategy

Previous modelling activity related to the “KOSI”-campaign was successful in the sense that the experiments could be well described by the models [2, 3]. However, a large variation of parameters between individual experiments impeded a proper understanding of phenomena that occur differently on comets than in the laboratory. Therefore, we pay special attention in the CoPhyLab campaign to repeating the most important baseline experiments. Moreover, we evolve the experiments from a simple form, where well characterized albeit idealized samples are used (e.g. glass beads), to more advanced iterations with more realistic analogue materials. On the one hand, this is to ensure that we understand the fundamental physical processes before considering complex interactions. On the other hand, the simple experiments provide us with the functional dependencies of thermophysical parameters (e.g. thermal conductivity) on the material properties, such as porosity, grain size distribution, grain shape and temperature.

Numerical Model

We approach the TPM analogously to the experiments, by starting with a very simplified macrophysical model using the finite element method (FEM). Thereby, the material-specific input parameters, which contain the microphysical relations, are taken from the characterization experiments. While most TPMs for comets are one-dimensional [2, 4], the consideration of special spatial features (e.g. sample boundaries, sensor hardware etc.) may require a 3D model [5]. To this end, we use the commercial FEM simulation software “COMSOL Multiphysics”, as it is ideally suited for our application. After the verification of our basic TPM with COMSOL, we will translate and evolve the model as a 1D code in python. This will provide a complementary, resource efficient method to simulate processes such as material ejection.

First Phase

In the first phase, we will establish the mathematical model that is required to describe the temperature evolution in a dry, well-defined sample (e.g. glass beads), illuminated in vacuum. A schematic of the corresponding experiment is shown in Figure 1. After satisfactory agreement between the model and experiment, more complex iterations will follow, for example by adding volatile phases and modelling their sublimation.

These investigations lead to a better understanding of effects in the cometary analogue material during measurements, and in addition, of effects related to the measurement setup and its interaction with the sample. As an extra benefit, a higher accuracy of future laboratory experiments in this context can be achieved.

Acknowledgements

This work is carried out in the framework of the CoPhyLab project funded by the D-A-CH programme (DFG GU 1620/3-1 and BL 298/26-1 / SNF 200021E 177964 / FWF I 3730-N36).

References

[1] Sears D. W. G. et al.: Laboratory simulation of the physical processes occurring on and near the
surface of comet nuclei, Meteoritics & Planet. Sci., 34, pp. 497-525, 1999.

[2] Spohn, T. and Benkhoff, J.: Thermal history models for KOSI sublimation experiments, Icarus Vol. 87, pp. 358-371.

[3] Benkhoff, J. and Spohn, T.: Thermal histories of the KOSI samples, Geophys. Res. Letters Vol. 18, pp. 261-264, 1991.

[4] Steiner, G. and Kömle, N. I.: A model of the thermal conductivity of porous water ice at low gas pressures, Planet. Space Sci. Vol. 39, pp. 507-513, 1991.

[5] Macher, W et al.: 3D thermal modeling of two selected regions on comet 67P and comparison with Rosetta/MIRO measurements, Astron. Astrophys., Vol. 630, id. A12, 2019.

How to cite: Laddha, S., Macher, W., Kargl, G., Zivithal, S., Pommerol, A., Blum, J., and Gundlach, B. and the CoPhyLab Team: Thermophysical Modelling of the CoPhyLab Experiments, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-528, https://doi.org/10.5194/epsc2022-528, 2022.

During the apparition of comet 67P/Churyumov-Gerasimenko (67P/C-G) solar irradiation causes varying rates for sublimation of volatile species from the cometary nucleus. Because sublimation processes take place close to the cometary surface, the relative abundance of volatiles in the coma and the ice composition are related to each other. To quantify this relation we assume a model for the expansion of a collisionless gas from the surface into the surrounding space. We use an inverse model approach to relate the in situ measurements of gas densities from the two Rosetta instruments COPS (COmet Pressure Sensor) and DFMS (Double Focusing Mass Spectrometer) at the positions of the spacecraft to the locations of surface gas emissions during the Rosetta mission 2014-2016. We assume the temporally integrated gas emissions to be representative for the ice composition close to the surface. Our analysis shows characteristic differences in the ice compositions between both hemispheres of 67P/C-G. In particular CO2 ice has a reduced abundance on the northern hemisphere. In contrast to the hemispherical differences, the two lobes do not show significant differences in terms of their ice composition.

How to cite: Läuter, M., Kramer, T., Rubin, M., and Altwegg, K.: Determination of the ice composition near the surface of comet 67P/Churyumov-Gerasimenko, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-826, https://doi.org/10.5194/epsc2022-826, 2022.

Introduction

Planetary systems form from sub-micron sized dust embedded in a mostly gaseous protoplanetary disk. Dust has to grow into planetesimals (∼ km sized objects) considered to be the building blocks of planets. We see reminiscences of these objects in the solar system small bodies, such as asteroids and comets, that have been left over from the planets genesis process. However, planetesimal formation is still one of the major open questions in planet formation theory. Solids can’t grow up to asteroid size relying only on sticking after pairwise collisions, due to the fragmentation barrier and the drift barrier [1]. The favoured solution is to form dense particle clumps, with low velocity-dispersion, that can then collapse under self-gravity. However the way in which the solids can be concentrated, e.g. streaming instability [2] or Rossby wave instability [3], is highly debated and can be modelled as a turbulent dynamic in the disk. To understand planetesimal formation it is then fundamental to study jointly the turbulent dynamics. In this context, we model the dynamics of particles in turbulent flows with Keplerian rotation and shear. To address this astrophysical problem we use fluid-dynamics methods to provide innovative perspectives on this challenging question.

Method

We model the dynamical evolution of the protoplanetary disk’s dust coupled to the gas phase. We perform 2D direct numerical simulations using a pseudo-spectral solver and the shearing box approach, in which the incompressible Navier-Stokes equation is solved locally with shear periodic boundary conditions. The gas is maintained turbulent through an external stochastic forcing. We use an Eulerian approach for the fluid while we implement the dust as Lagrangian particles. We explore various values of the rotation frequency Ω and the solid response time τ , a parameter related to the particle size. We analyse the results using tools borrowed from the study of dynamical systems.

Fractal and strong clustering of solids

In order to characterize the dust dynamics in the flow and to identify in which case there is a strong concentration of the solids that could lead to small body formation, the Lyapunov dimension dL is calculated for each run (Fig. 1a). This quantity gives an estimation of the fractal attractor dimension in the phase space [4]. We find three different regimes. At low rotation rate and for large particle size we obtain dL > 2, therefore the inertial particles fill the whole space. Focusing instead on intermediate values of the response time, for small rotation rates the particles are expelled from the eddies and form fractal structures (Fig. 1b), while they tend to concentrate inside the anticyclones for larger Ω (Fig. 1c). Particles eventually form a pointwise cluster for dL = 0 (Fig. 1d).

We then inspected the mass distribution of solids in the domain. Analysing a case that falls into the strong clustering regime (Ω=64/3, τ=0.05) we find that the different clusters of particles tend to merge with time to form a unique pointwise cluster at the end of the simulation (Fig. 2a). In order to estimate the interaction strength between sets of n particles, we then calculated the fractal dimensions Dn for different values of the rotation frequency and the solid response time (Fig. 2b, Fig. 2c). This dimensions characterize the anomalous scaling typical of multifractal attractors [5]. We notice that for the strong clustering case (Fig.2b, Ω=64/3) the attractor is homogenous with its fractal dimension Dn = 0 for all n. We instead find that when particles cluster fractally the attractors are multifractals that show decreasing values of Dn with increasing n. This behaviour at large n is particularly interesting for the gravitational collapse of dust: it means that particles in numerous groups will interact strongly, therefore possibly collapsing under self-gravity to form a planetesimal.

Conclusions and future perspectives

We have identified promising tools for the understanding of planetesimal formation. We also showed how the behaviour of dust particles in a turbulent flow drastically change with increasing rotation rate, leading to the formation of strong dust clumps. In the future the back-reaction from dust on gas will be added, particularly important for triggering the streaming instability. Self-interaction between solids particles (e.g. collisions, gravity) will also be considered to study how dust in vortices can accrete and form large aggregates.

Figure 1: a) Phase diagram of the rotation frequency Ω vs the particle response time τ . The colour-code is for the Lyapunov dimension dL. b) Snapshot of dust particles position and fluid vorticity at t=200 for Ω=4/3 and τ=0.1 c) for Ω=32/3 and τ=0.1. d) for Ω=80/3 and τ=0.1.

Figure 2: a) Path of different clusters of particles along time for Ω=64/3 and τ=0.05. b) Fractal dimension Dn as a function of the order of the fractal dimension n for different  values of rotation frequency Ω and τ=0.025 c) and τ=0.5.

Bibliography

[1] L. Testi, T. Birnstiel et al., Dust Evolution in Protoplanetary Disks, Protostars and Planets, IV, 339-361 (2014).
[2] A. N. Youdin and J. Goodman, Streaming Instabilities in Protoplanetary Disks, The Astrophysical Journal, 620, 459–469 (2005).
[3] R. V. E. Lovelace, S. A. Colgate, A. F. Nelson, Rossby Wave Instability of Keplerian Accretion Disks, The Astrophysical Journal, 513, 805-810 (1999).
[4] J.L. Kaplan and J.A. Yorke, Chaotic behavior of multidimensional difference equations, Proceedings on Functional Differential Equations and Approximation of Fixed Points, 730, 204-227 (1979).
[5] G. Paladin and A. Vulpiani, Anomalous scaling laws in multifractal objects, Physics Reports, 156, 147-225 (1987).

How to cite: Gerosa, F. A., Méheut, H., and Bec, J.: New approach to planetesimal formation: clusters of heavy particles in two-dimensional Keplerian turbulence, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-462, https://doi.org/10.5194/epsc2022-462, 2022.

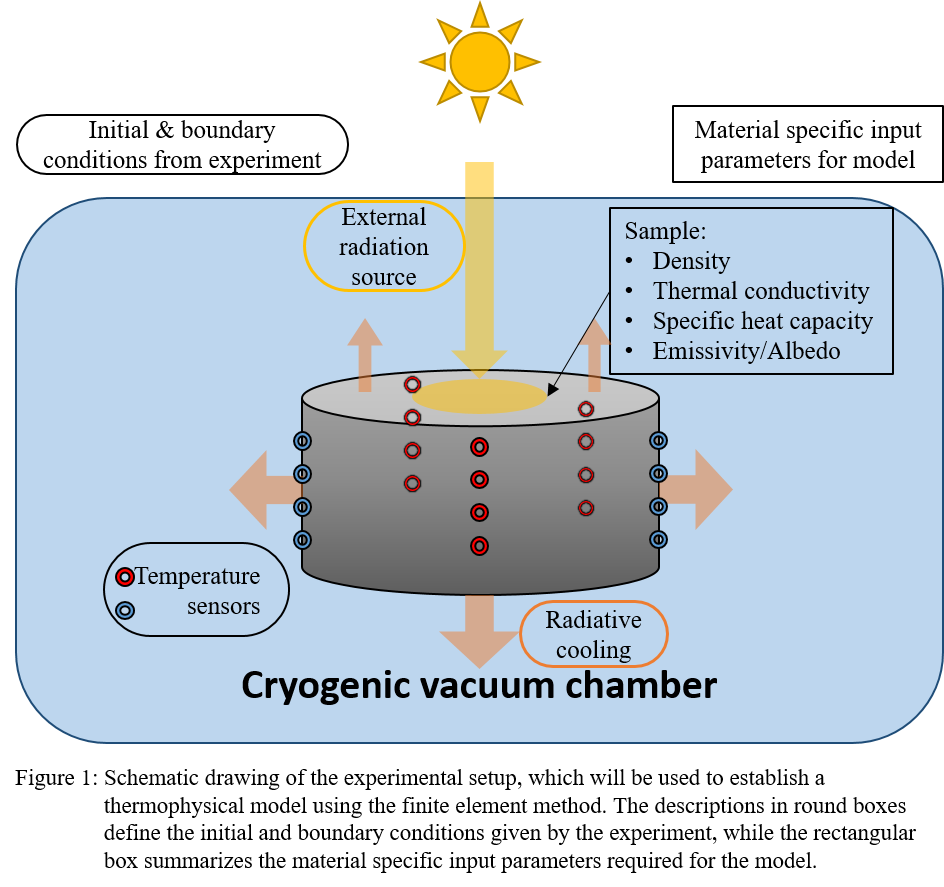
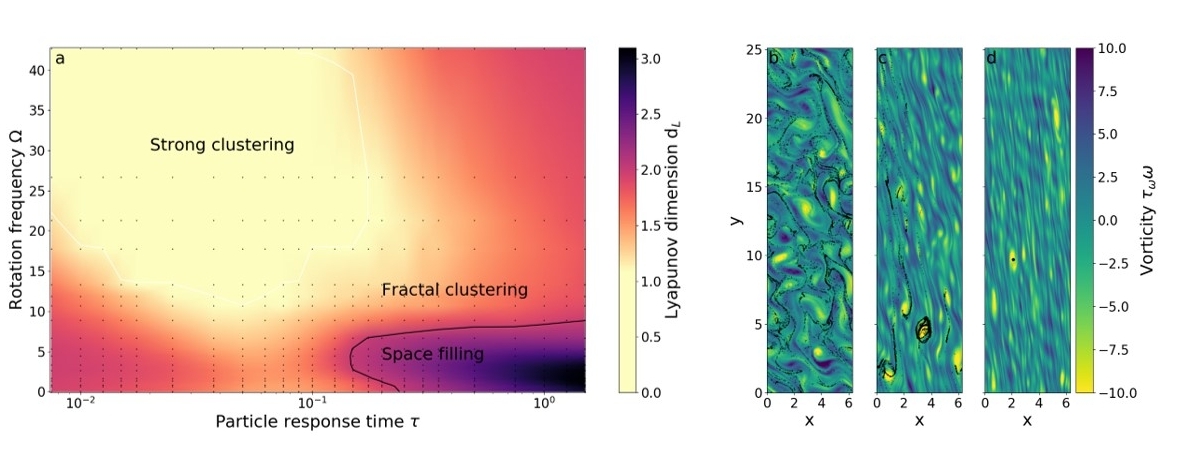
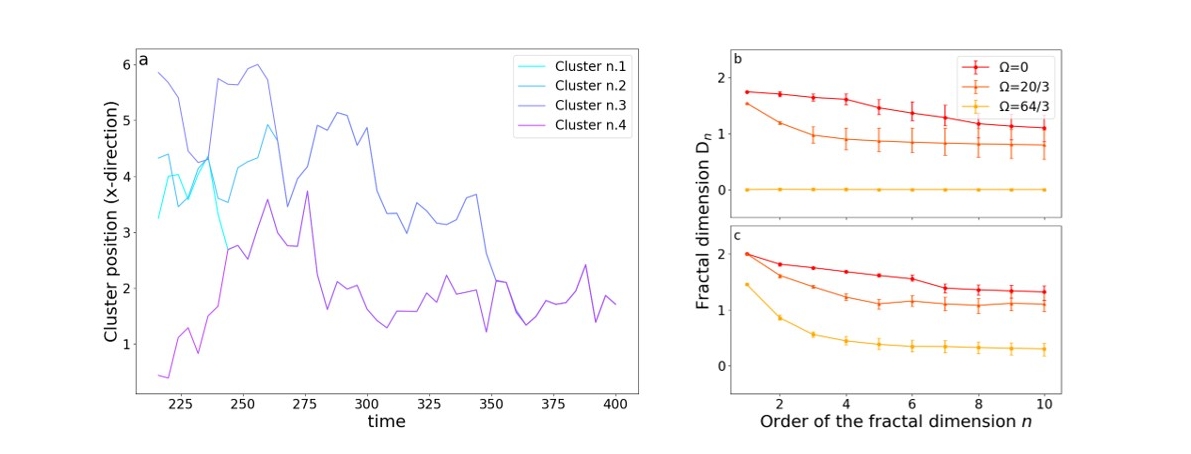
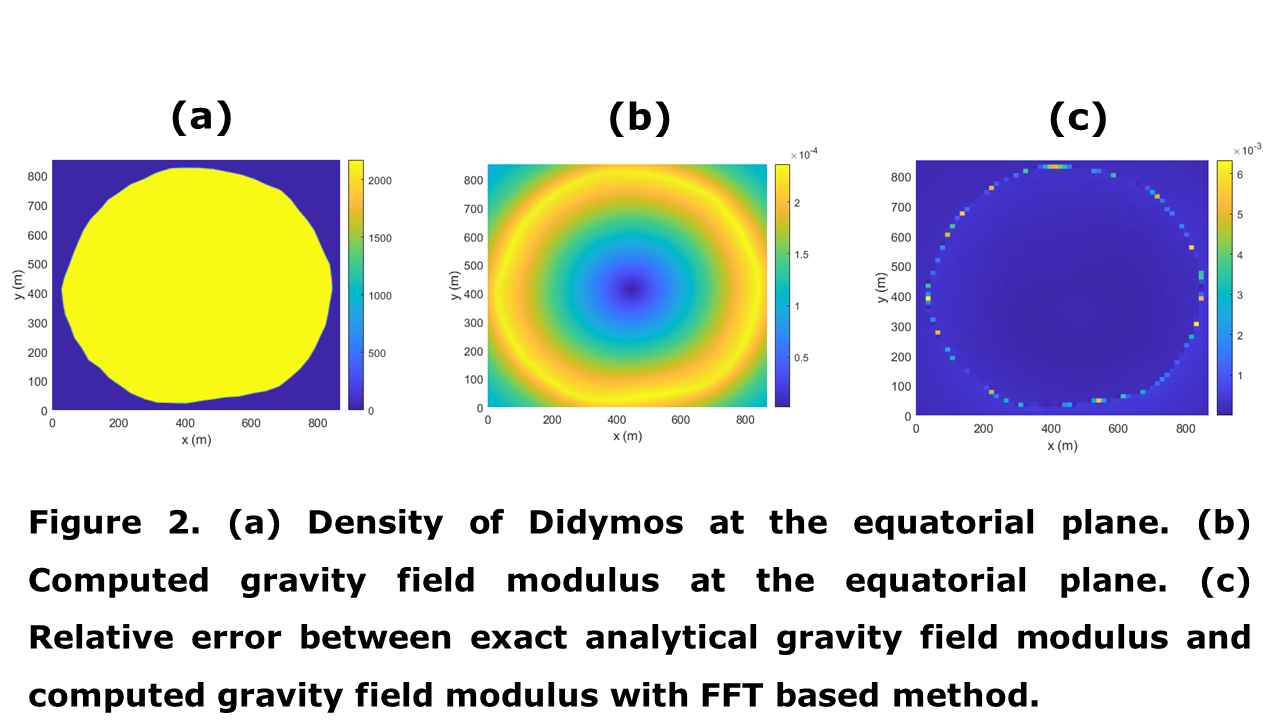
Many objects that form via a gravitational collapse or contraction appear to rotate around their own axis (spin) in a manner that aligns with their orbit around larger parent structures. Systematic prograde rotation is found in the planets and larger asteroids of the Solar System [1], in the stars of several open clusters [2], as well as in the molecular clouds of different galaxies [3,4]. Remarkably, the fact that such a spin-orbit alignment exists across different scales has received little scientific attention in the last decades, while a satisfactory answer remains to be found.

Indeed, when the rotational direction of an object is assumed to be equal to that of the cloud from which it formed, only specific birth environments with rising orbital velocity curves lead to systematic prograde spin [5]. We present a new mechanism that describes how collections of particles or clouds gain a prograde rotational component when they collapse or contract while subject to an external, central force. We show that because particles that orbit in any non-rigid cloud shear away from one another over time – and do so on curved paths – their combined center-of-mass moves inward. The orbital angular momentum that is thus liberated, adds a prograde component to the spin of the object that forms. 

We first visualize the mechanism of prograde spin-up in Fig. 1a, where we plot the motion of a disk of particles on circular orbits around a central mass. For illustrative purposes, mutual interactions like self-gravity are not included here. Over time, the shear over curved orbits morphs the particles into an increasingly extended arc, whose combined center-of-mass moves inward to an orbit with a reduced semi-major axis. Hence, if the cloud of particles were to gravitationally collapse, the object forms at an orbit interior to the cloud, with a lower orbital angular momentum. The deficit goes into rotation, and the object attains a prograde spin. Being a geometric effect, the mechanism of prograde spin-up persists around any central potential that triggers shear, even those where the shear is strongly retrograde.

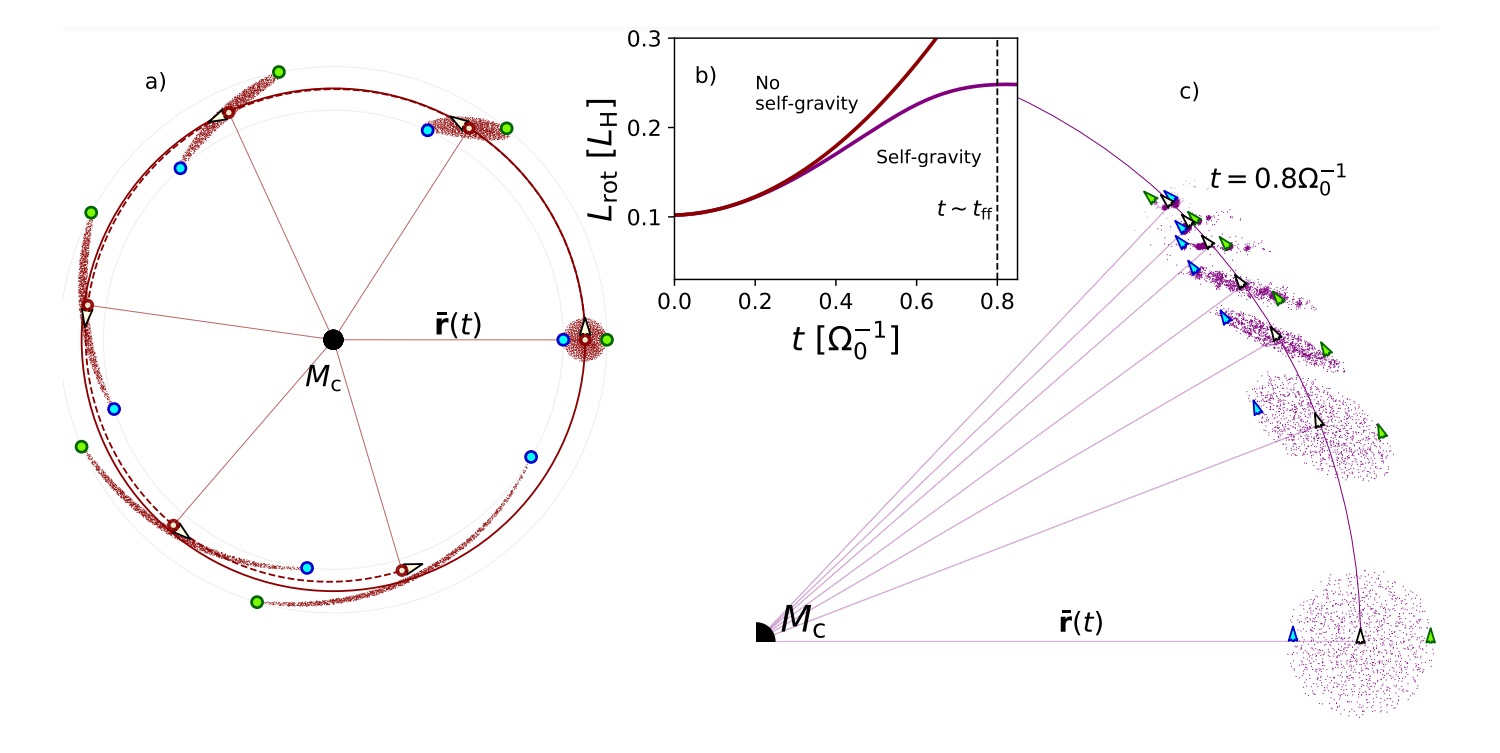
Fig. 1: Visual representation of the prograde spin-up mechanism

To verify this mechanism of prograde spin-up, we perform N-body simulations of gravitationally bound, collapsing clouds with REBOUND [6]. As seen in Fig. 1b, the rotational angular momentum of the cloud increases quadratically during the collapse (δL_rot/L_H ∝ t²), before slowing down when the collapse completes around t ∼0.8 t_ff in this example. We provide further visualization in Fig. 1c, where shear is seen to initially deform the cloud into a curved, bar-like structure whose center moves inward, spinning up the material. As the cloud contracts, collisions prevent further relative motion and eventually a stable, prograde binary forms.

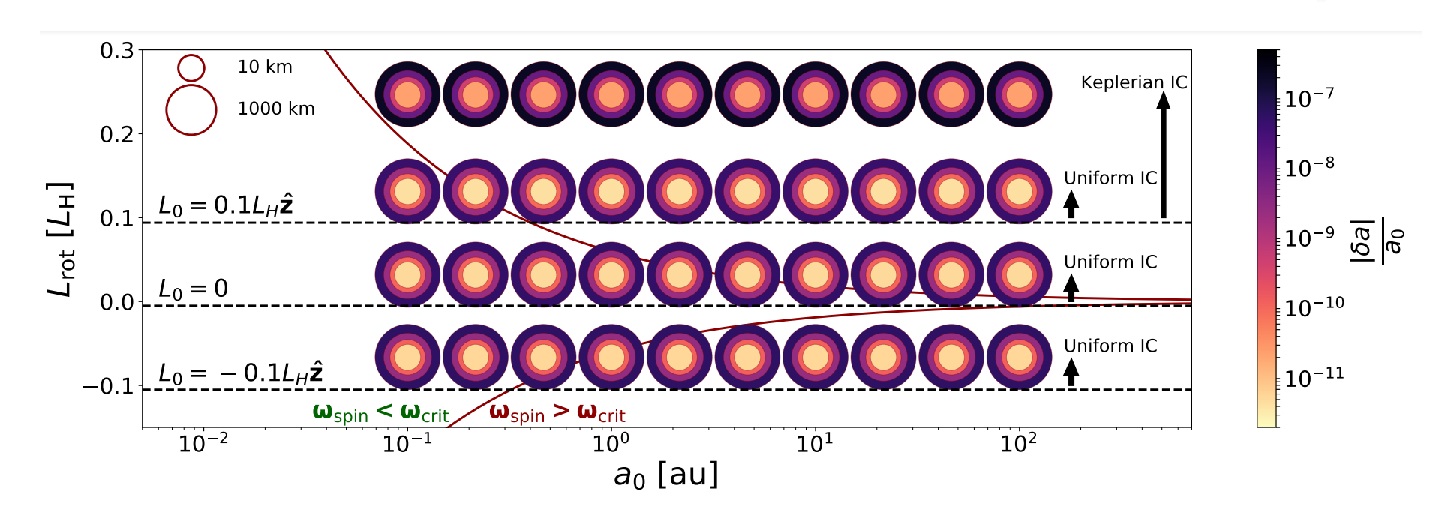
Fig 2: Rotational gain by prograde spin-up in the streaming instability.

We highlight an application of prograde spin-up to the rotation of (binary) asteroids in the Solar System, which are understood to form via gravitational collapse in a process known as the streaming instability [7]. We numerically estimate the magnitude of their spin-up with a set of N-body simulations with varying initial conditions (see Fig. 2). The formation of binaries is easier in the outer Solar System, offering an explanation for the high fraction of binary systems on wider orbits. Indeed, we show that at the distance of the Kuiper belt (∼30 AU), even the clouds that begin their collapse without any rotation can gain enough angular momentum via prograde spin-up to form prograde comet binaries.

Within the Solar System, the group of 'Cold Classicals' that reside in the Kuiper belt provide a unique sample of asteroids that likely retained their rotation at birth [8]. Besides being characterized by low inclinations and eccentricities, this group contains a high fraction of binary pairs [9] that often have strong color correlations [10], reinforcing the idea that they formed in a single gravitational collapse – rather than by later capture. The majority of these binaries spin in a prograde direction, a key signature that has recently been reproduced with detailed hydrodynamical simulations [8,11]. In these simulations, the colatitude distribution of the vorticity vectors is initially broad, and the prograde bias only appears when the bound clumps collapse. We suggest that the new mechanism of prograde spin-up can function as the physical driver of this rotational bias. 

The relevance of prograde spin-up to the formation of objects by gravitational collapse on larger astrophysical scales remains open for further investigation. It is likely, however, that the universal applicability of prograde spin-up contributes to the ubiquity of spin-orbit alignment on different scales. The total rotational gain scales with relative cloud size: δL_rot/L_H ∝(R_cl/R_H)⁵. Compared to the rotation contained in shear: δL_rot/L_H ∝(R_cl/R_H)², prograde spin-up becomes important when the size of the cloud prior to collapse is comparable to the Hill radius. For objects that form in this interface between self-gravity and shear, prograde spin-up naturally produces a spin-orbit alignment, even in an environment of retrograde shear.

[1] Grundy, W. M., Noll, K. S., Roe, H. G., et al. 2019, Icarus, 334, 62

[2] Corsaro, E., Lee, Y.-N., García, R. A., et al. 2017, Nature Astronomy, 1, 0064

[3] Braine, J., Rosolowsky, E., Gratier, P., Corbelli, E., & Schuster, K. F. 2018, A&A, 612, A51

[4] Braine, J., Hughes, A., Rosolowsky, E., et al. 2020, A&A, 633, A17

[5] Mestel, L. 1966, MNRAS, 131, 307

[6] Rein, H. & Liu, S. F. 2012, A&A, 537, A128

[7] Johansen, A., Youdin, A., & Mac Low, M.-M. 2009, ApJ, 704, L75

[8] Nesvorný, D., Li, R., Simon, J. B., et al. 2021, Planetary Science Journal, 2, 27

[9] Grundy, W. M., Noll, K. S., Roe, H. G., et al. 2019, Icarus, 334, 62

[10] Benecchi, S. D., Noll, K. S., Grundy, W. M., et al. 2009, Icarus, 200, 292

[11] Nesvorný, D., Li, R., Youdin, A. N., Simon, J. B., & Grundy, W. M. 2019, Nature Astronomy, 3, 808

How to cite: Brouwers, M. and Visser, R.: Prograde spin-up during gravitational collapse, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-582, https://doi.org/10.5194/epsc2022-582, 2022.

Introduction
Evidence from in-situ and remote observations supports the idea that asteroids are rubble piles, i.e., gravitational aggregates of loosely consolidated material (Chapman 1978; Hestroffer et al. 2019). However, no direct measurements of asteroids’ interior exist, and little is known about the mechanisms governing their formation and evolution. To date, only a handful of asteroids have been visited by space probes. Compared to remote surveys, these provided important and unprecedented data, although focused on very specific asteroids. Recently, NASA's OSIRIS-REx and JAXA's Hayabusa2 revealed unexpected features on the surfaces of respectively, asteroids Bennu and Ryugu (Lauretta et al. 2019; Watanabe et al. 2019) and showed that constitutive relations derived from Earth-based experiments, or from previous in-situ measurements can hardly scaled up and re-adapted to different asteroid scenarios (Arakawa et al. 2020; Ballouz et al. 2021). Not only limited by a lack of data, the understanding of asteroids’ properties is challenged at a fundamental level by their rubble-pile nature. This makes their dynamics subject not only to the complex N-body gravitational interactions between its constituents, but also to the laws of granular mechanics, which is one of the major unsolved problems in physics.
To mitigate these limitations, we propose here the use of dynamical system theory to study these complex N-body/granular systems, where the dynamics of individual bodies are driven both by mutual gravity and contact/collision interactions. The goal of this work is to investigate the feasibility of using chaotic indicators to infer the dynamical properties and transitions of granular systems. In particular, we implement the methodology and apply it to systems of granular aggregates, in the context of rubble-pile asteroid dynamical scenarios.

Methodology
We develop here a new theoretical framework to support the qualitative and quantitative investigation of dynamical transitions in a complex N-body/granular system. With the term "N-body/granular system", we refer to systems made of several fragments that interact mutually through self-gravity and contact/collisions. These fragments have finite density and irregular shape, and reproduce particles in a granular media. The theoretical framework is based on the global representation of the behavior of the system by using chaotic indices. We define here several chaotic indices, including Finite-Time Lyapunov Exponents and Lagrangian Descriptors (Mancho et al 2013), both customized to the problem studied here, and test their suitability to identify the qualitative and quantitative behavior of the N-body granular system. In particular, we focus on applications related to rubble-pile asteroid scenarios. We test the newly developed theoretical framework against high-fidelity numerical simulations, which are considered here as ground-truth model of the reality. This choice is motivated by the lack of real-world and full-scale data. Also, we highlight that theoretical models such as the continuum model provide major simplification of the granular nature of the system and thus are not sufficiently accurate to be considered as real-world models. Nonetheless, existing theoretical models provide a useful mean of comparison and will be referenced throughout the analysis in this paper.

Results
As a test case, we reproduce the dynamics of a spinning rubble-pile aggregate, within a large parameter space including a range of different bulk densities and spin rates. We use chaotic indicators to build stability maps, to identify transitions in the dynamical behavior of the aggregate. These are used to identify limiting values in the density and spin rate which make the aggregate either stable or unstable, i.e., to identify its breakup limits.
Preliminary results show good agreement between predictions based on chaotic indices and our ground-truth model, based on high-fidelity numerical simulations. In particular, Finite-Time Lyapunov Exponents appear to be better suited to identify complex transient motion within the aggregate, while Lagrangian Descriptors are shown to provide faster identification of the aggregate's breakup limit dynamical transition. Most notably, transition maps are shown to evolve in time, following the complex and dissipative nature of the N-body/granular system. Finally, we compare predictions based on chaotic indicators with the theory of continuum, which identify disruption limits of gravitational aggregates based on the simple static relation ω_lim=√(Gρπ); where ω_lim is the spin rate limit before breakup and ρ is the bulk density of the aggregate.

Figures show examples of transition maps using Finite-Time Lyapunov Exponent (upper figure, red line indicates FTLE=0) and Lagrangian Descriptor (lower figure), both based on the time evolution of the polar inertia of the system. In the Figures, the breakup curve for continuum is shown using a blue dashed line.

Conclusion
Our results provides a proof-of-concept to support the conceptual validity of our hypothesis, and demonstrate the capability of our newly proposed methodology to identify dynamical transitions in N-body/granular systems. In particular, we applied it to the case of spinning rubble-pile asteroids, to investigate their rotational breakup. This work represents a first step towards the generalization of our theoretical framework to other dynamical scenarios involving the formation and evolution of rubble-pile asteroids.

References
Chapman 1978, In Asteroids: An Exploration Assessment. NASA Conf. Publ. 2053.
Hestroffer et al. 2019, A&A Rev. 27
Lauretta et al. 2019, Nature 568
Watanabe et al. 2019, Science 364
Arakawa et al. 2020, Science 368
Ballouz et al. 2021, Mon Not R Astron Soc 507
Mancho et al. 2013, Comm Nonlin Sci Num Sim 18

How to cite: Ferrari, F. and Alessi, E. M.: Dynamical transitions in the N-body granular problem to identify breakup limits of rubble-pile asteroids, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-162, https://doi.org/10.5194/epsc2022-162, 2022.

Recent sample-return missions to asteroids (101955) Bennu and (162173) Ryugu have revealed their rough surfaces are strewn with regolith particles ranging from millimeters to tens of meters in diameter with a broad spectrum of shapes. Numerical modelers often simulate these kinds of bodies as rubble piles composed of discrete particles with rock-like material properties. The particles in most models for the past few decades have been independent spheres meant to represent the individual grains that make up the surface and interior of a rubble pile. It has been shown, however, that grain shape has a significant effect on the flow and equilibrium states of particles in granular media. Simulating irregular grain shape is thus imperative for accurately modeling the surfaces and interiors of rubble-pile asteroids.

One of the most challenging aspects of simulations using spherical particles is creating high-porosity media. The densest packing distribution of monodisperse spheres has ~26% porosity; porosities of polydisperse spheres in a randomly packed orientation approach 35-45%. Bennu and Ryugu were each found to have bulk densities on the order of 1.1 g/cc, indicating bulk macroporosities of 50% or larger. Furthermore, the depth to which the arm of the OSIRIS-REx TAGSAM spacecraft penetrated Nightingale crater showed that it met little resistance from the regolith surface of Bennu, which may indicate that the finer-grained parts of regolith surfaces could have porosities larger than the bulk macroporosity. The low bulk densities and high macroporosities of rubble piles that have been visited by spacecraft seem to indicate subsurface structure mainly supported by contact networks between regolith grains strengthened by grain shape and interparticle cohesion from electrostatic and van der Waals forces. These recent results, in combination with historical measurements on the lunar surface, show a need to be more methodical in preparing “fluffy” granular beds to accurately reproduce surface structure on low-gravity, airless bodies.

For our experiments, we use the parallel N-body gravity tree code PKDGRAV. PKDGRAV uses a soft-sphere discrete element method to model surface grains as individual spheres that feel interparticle and uniform gravity, cohesion, and contact forces. The contact forces from the soft-sphere method allow particles to slightly interpenetrate at the point of contact, using a restoring spring force to model the stiffness (akin to the Young’s modulus) of the material and applying normal and tangential damping and forces like interparticle friction. More recently, we have made improvements to routines handling irregularly shaped “aggregate” particles, made by “gluing” together two or more spheres.

Aggregates allow PKDGRAV users to capture geometric effects like bulking, where low-sphericity polyhedra generally occupy larger volumes than spheres when packing, accounting for increased porosity and resistance to flow in granular media. With this in mind, we model the gentle deposition of aggregates under microgravity and lunar gravity to create highly porous (>50% porosity) granular assemblies both with and without cohesion. We use aggregates composed of centimeter-scale spheres and model both symmetric and asymmetric shapes, as well as systems with both aggregates and single spheres. We calculate the porosity of these systems by generating a concave hull around the settled system and calculating the ratio of the total volume in particles interior to the hull to the total hull volume, with interior particle volume modified to account for particle-particle overlaps and particle fractions partially exterior to the hull.

How to cite: DeMartini, J. and Richardson, D.: Modeling High-Porosity Regolith on Low-Gravity Planetary Surfaces, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-560, https://doi.org/10.5194/epsc2022-560, 2022.

Introduction: Scheduled to be performed in September 2022, the DART (Double Asteroid Redirection Test, NASA) mission will be the first-ever space mission to demonstrate asteroid deflection by crashing an impactor spacecraft into a binary NEA target: the moon of (65803) Didymos, called Dimorphos. In the frame of the studies related to the EC-H2020 NEO-MAPP project, we perform numerical simulations of the collision event on Dimorphos without the presence of Didymos by using the N-body numerical code, PKDGRAV [1] with an implementation of the soft-sphere discrete element method [2], under the assumption that it is a spherical gravitational aggregate produced in the formation of the binary system [3, 4]. The very structure of the target is unknown; therefore, we model it by (a) 100550 mono-dispersed spherical particles in a close hexagonal packing (hereafter mono-CHP) configuration, with particle radii of 1.5 m; (b) multi-dispersed distribution of 100000 spherical particles in a random packing (hereafter multi-RP) configuration, with particle radii ranging from 1 to 2.5 m.

Method: The real DART impact should be a hyper-speed cratering event where most impact kinetic energy goes into the shattering phase including asteroid local material damage like vaporization, melting, rock deformation, heat transfer, and so on. However, due to the fact that PKDGRAV is not able to simulate the shattering phase, we instead concentrate on the effect of the collision on the target, once the shattering phase is over. Therefore, our synthetic projectile needs to deliver the same nominal linear momentum to Dimorphos as the DART spacecraft will do, but it delivers to the target only a small fraction of kinetic energy expected to survive once the shattering phase has dissipated most of the impact kinetic energy (non-elastic collision). According to the cratering experiments [5], only a small fraction of impact energy will go into the kinetic energy of the target after the shattering phase. This residual kinetic energy is about 0.25% of the initial impact energy.

For the multi-RP case, we also account for different centre and off-centre impact geometry compatible with DART nominal impact angle (20º) with respect to the target orbital plane, considering the possibility that the real DART spacecraft may not impact exactly toward the centre of Dimorphos.

Results: From all of our cases, we find that none of the cases can transmit the impact kinetic energy to the other side of the impact point. However, particle movements in the antipodal hemisphere of the impact are possible even without impact energy reaching there because the aggregate tries to reach a new equilibrium shape after the relatively large crater and deformation were generated by the DART impact. As a result, the surface particles in the antipodal hemisphere move toward the crater, causing the particles to sink into the ground. 
In the antipodal hemisphere, we found all the particles have negative vertical displacements typically around -1 m and can be up to around -2 m. The center of the surface depression is very close to a longitude and latitude of 0° and 20° because the center of the crater is at 180° and 20° longitude and latitude, which is the antipodal point.

The surface particle movements have both vertical and horizontal components. We found many particles in the northern region have horizontal displacements larger than 1 m and can be up to 3.2 m. It takes tens of minutes or a few hours for the particles to settle down and reach their final locations. On the other hand, at about 3 mins after the impact, LICIACube will be able to take images on the antipodal side of the impact, with a resolution of about 1.5 m. None of the surface particles can have horizontal displacements larger than 1.5 m at that time, therefore LICIACube will be essentially taking images of the original locations of the boulders on the antipodal side of the impact.

We therefore predict that by comparing the LICIACube and Hera observations, it is possible to obtain the real horizontal displacements of the boulders. The exact displacements caused by this resurfacing process depend on several internal material parameters and also on the level of deformation of Dimorphos by the real impact, and thus the observation may give information about the internal structure of Dimorphos.

References:

[1] D. C. Richardson et al. (2000). Icarus, 143, 45.

[2] S. R. Schwartz et al. (2012) Granular Matter 14, 363.

[3] A. Campo Bagatin et al. (2001) Icarus, 149-1, 198. 

[4] A. Campo Bagatin et al. (2018) Icarus, Volume 302, 343.

[5] D. W. Walker (2013) Int. J. of Impact Engin. 56, 12.

How to cite: Liu, P.-Y., Campo Bagatin, A., Benavidez, P. G., and Richardson, D. C.: Resurfacing of Dimorphos in the Antipodal Hemisphere of the DART impact., Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-707, https://doi.org/10.5194/epsc2022-707, 2022.