Benchmarking Bayesian methods for spectroscopy

Introduction: Spectroscopic data is rich and powerful to study surfaces. Besides, planetary surfaces are often made of intimately mixed components [1, 2], so modelling a reflectance spectrum will mean fitting a relatively large number of inter-related parameters: at least, one proportion and one grain size for each component in the case of a granular mixture, plus structure parameters (roughness, porosity). In these large parameters spaces, it is highly possible that multiple solutions give an equally satisfactory fit [3]. It is crucial to evaluate the ability of a method to retrieve multiple solutions when setting up an inversion strategy.

 

Data: This work was done in the context of revisiting the Europa Galileo NIMS dataset. We compared the solutions of different methods on a radiative transfer model, based on Hapke modeling [1] and an observation of a bright region of Europa NIMS cube 14e006ci [4] with 4 components : crystalline ice, hexahydrite, magnetite and sulfuric acid octahydrate. The uncertainty on the data is assumed to be gaussian with a standard deviation at 10% with a minimum at 0.01 in reflectance.

Method: The parameters space is on dimension 9, with 8 independent parameters: 4 abundances, 4 grain sizes and the surface roughness. We noted early in our work that while reproducing the data equally well, two minimisations algorithm would give different results for the parameters, meaning the solution is not unique. To explore the set of possible solutions, four methods were compared: (i) home-made Markov Chain Monte-Carlo (MCMC) method with metropolis hasting sampler [5] (ii) home-made MCMC method with improved metropolis-hasting sampler [this work] (iii) open-source multi-chain MCMC algorithm with "snooker" sampler [6] (iv) multiple minimizations, using ”L-BFGS-B” bound-constrained algorithm with random initialisations [7].

To be able to compare the efficiency of the different methods, we limited the number of direct model evaluations to 1.5.10⁶. This number was chosen for 2 reasons: (i) each algorithm tested seemed to have reached "convergence": increasing the number of iterations did not change significantly the result, and (ii) identical and affordable computational cost between the methods. This means that for MCMC methods, we set the number of iterations to 1.5.10⁶. For the multiple minimizations method, each minimization resulted in approximately 1500 model evaluations to reach the result. So we performed 1000 minimisation with 1000 different random initialisations. For each of the model evaluation, a likelihood is computed, making the comparison between this method and the bayesian ones possible.

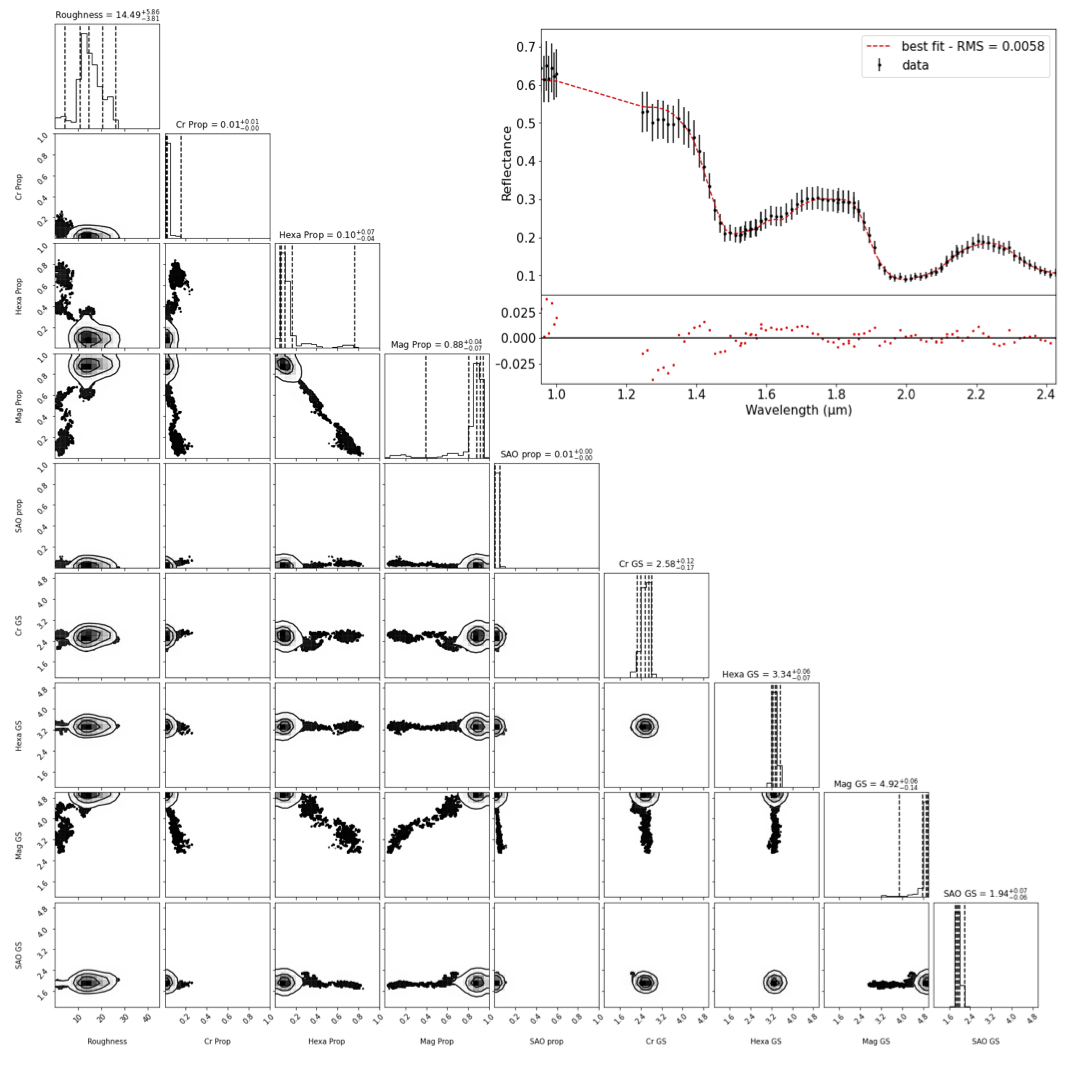
Figure 1: Corner plot and best fit for home-made MCMC method with Metropolis-Hasting sampler with a converged chain of 1.5 10⁶ iterations. The sampling is done with 3 cases: agnostic uniform distribution over the full prior space, in far neighbourhood, in close neighbourhood. The corner plot represents the pairwise posterior distributions, and the marginal posterior distributions for each parameter. Parameters are from left to right roughness, 4 abundances, 4 grain sizes and from top to bottom 4 abundances and 4 grain sizes. Acceptance rate is 0.217.

 

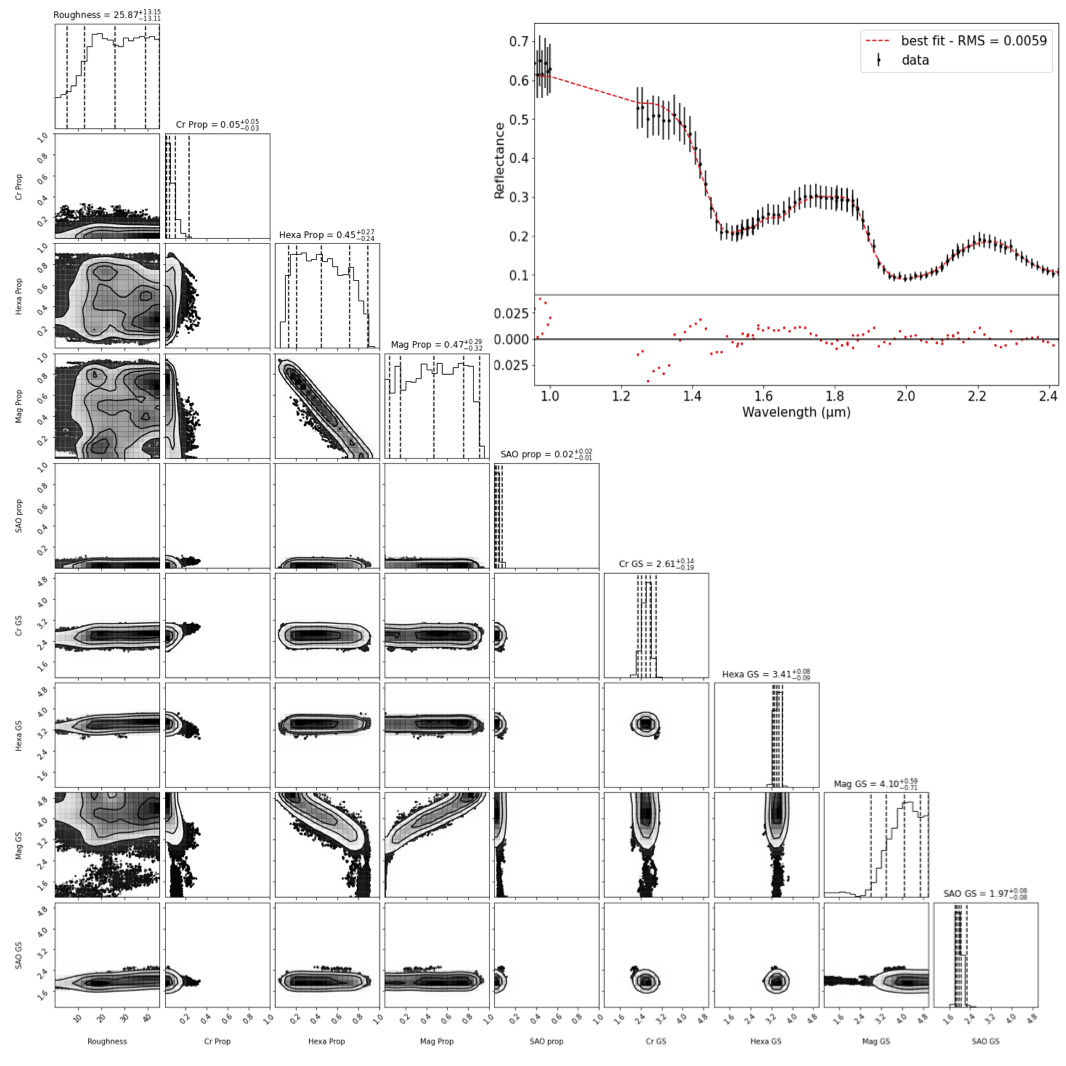
Figure 2: Same as fig 1 but in this case the sampling is done with 4 cases: agnostic uniform distribution over the full prior space, in far neighbourhood, in close neighbourhood, 1 single parameter modification.  Acceptance rate is 0.288.

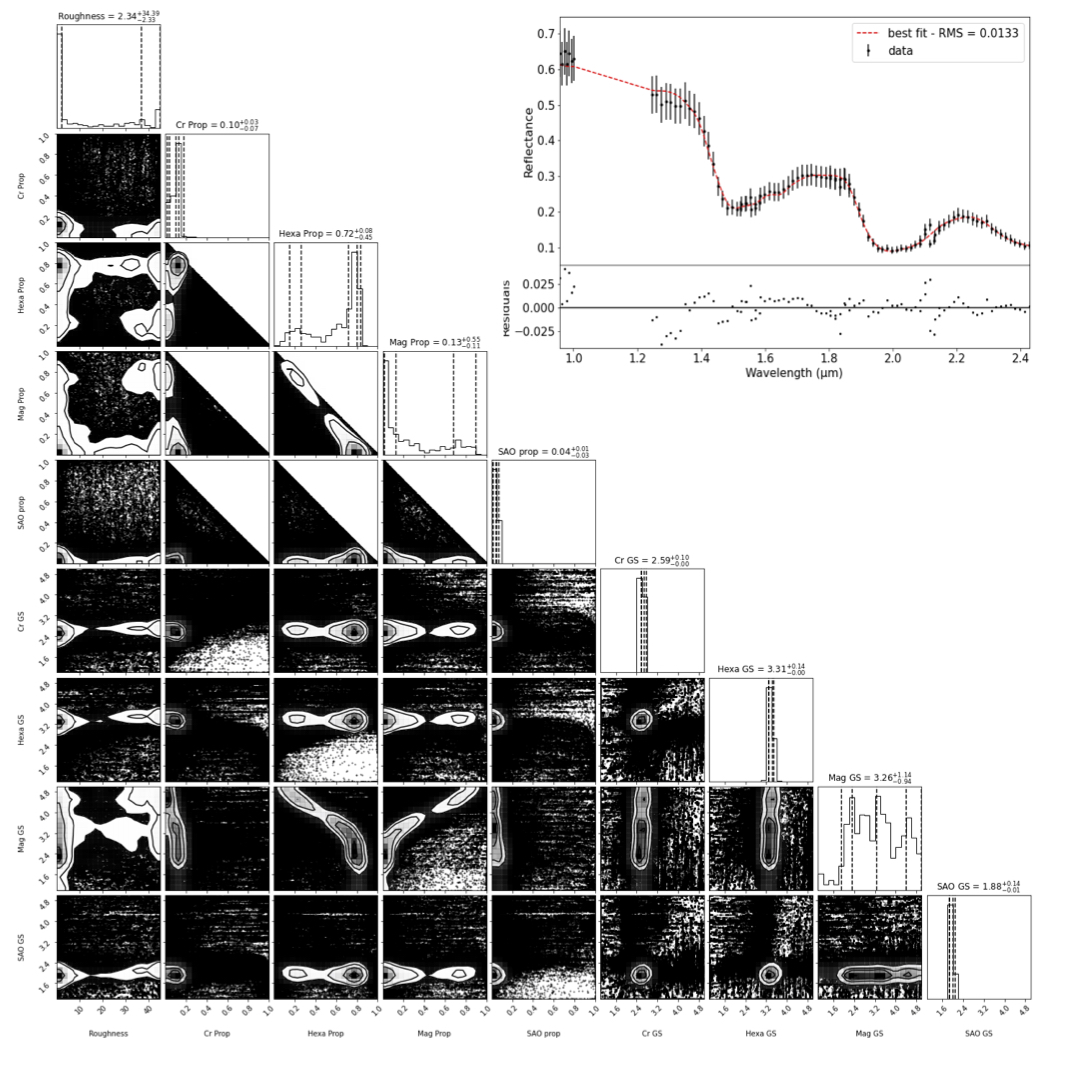
Figure 3: Same as Fig1 but  for 1000 multiple RMS minimisations with random initialisations. The 1500 points for each path has been recorded and converted into likelyhood to build the posterior distribution.

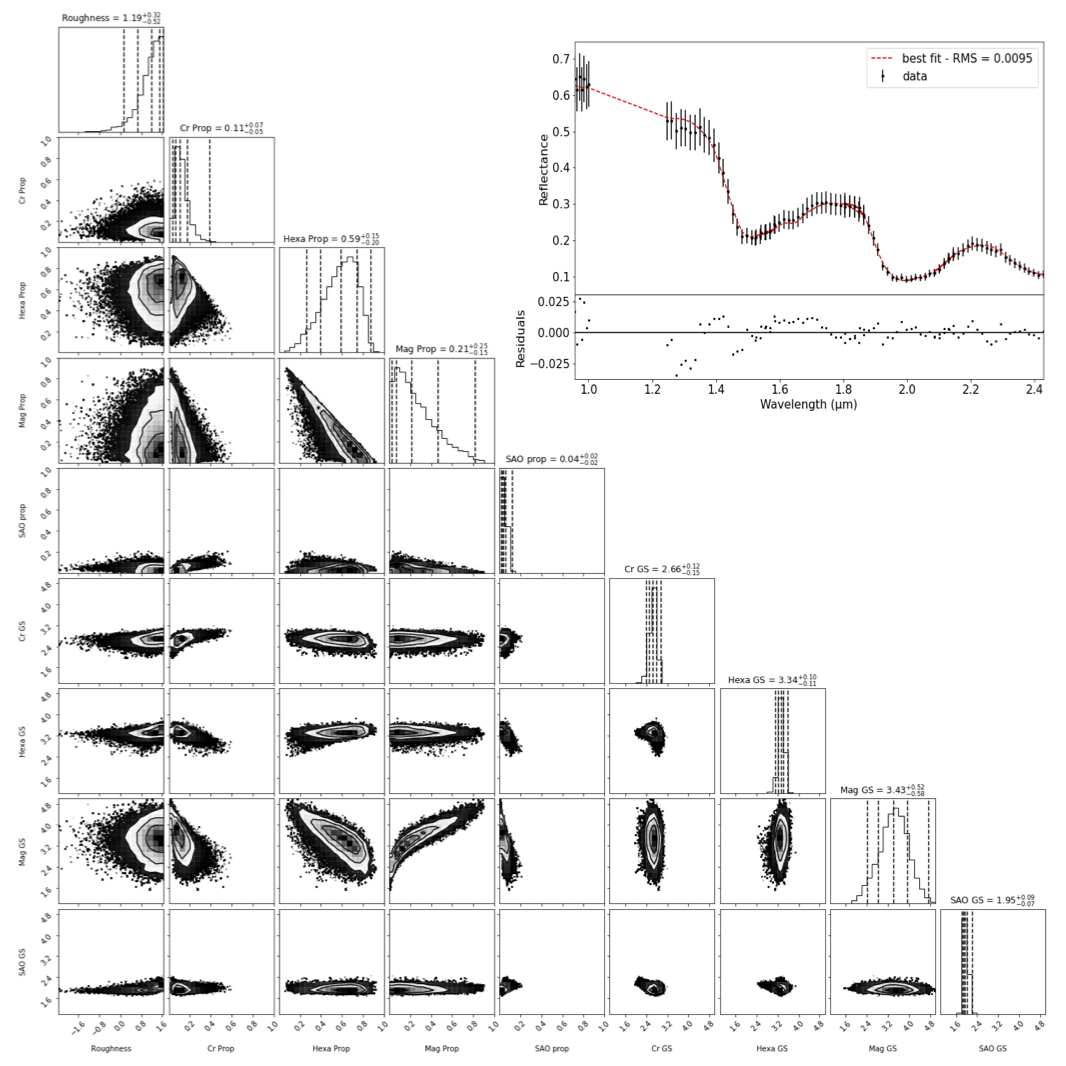
Figure 4: Same as Fig. 1 using the SNOOKER algorithm. Acceptance rate is 0.217.

Results: Three proxies must be compared when evaluating the perfomance of each method: quality of the best fit, posterior distribution, and computational efficiency. The results for the best fits and posterior distributions are displayed in figures 1-4: all methods manage to reproduce the data equally well. Nevertheless, the posterior densities are different. On these corner plots, each black dot is a point in the parameter space that has been computed (1.5 10⁶), but only the densities (solid lines) are relevant (with a non-negligible likelihood). The first method with home-made MCMC clearly fails to find a posterior distribution in agreement with others methods. It mean it "gets stuck" in a local solution, and the sampler fails to explore properly the parameters space. The three other methods show a relatively good agreement. On the numerical cost, we showed that lowering the number of model evaluations for the home-made MCMC with improved metropolis hasting sampler, and for the multiple minimisations method would significantly alter the results, while increasing the number of model evaluation, would not, meaning both methods are of equivalent numerical performance. The results of the open source multi chain MCMC method with snooker sampler were not significantly altered down to 2.10⁵ iterations, meaning it is almost 10 times more efficient than the other methods to retrieve surface properties.

Conclusion: Four inversion strategies have been compared to retrieve surface properties of Europa using a radiative transfer model inversion. This work showed the significant improvements of the multi-chain MCMC method using the SNOOKER sampler, compared to others. This method will be used in future work. In addition, this work stresses the fact that even MCMC sampler are by construction asymptotically sampling the posterior distribution, they may present an apparent converged chain that is actually biased. 

This study may be extrapolated to other datasets, and other models, with large parameters spaces (at high dimension), and correlated parameters, such as photometric inversions.

 

References:

[1] Hapke, 2012 Cambridge Univ. Press [2] Douté & Schmitt, 1998 JGR. [3] Schmidt & Fernando, Icarus, 2015 [4] Cruz-Mermy et al., 2022 EPSC. [5] Schmidt & Bourguignon , Icarus 2019 [6] Cubillos et al. (2016), The Astr. Jour. [7] Byrd et al., 1995 SIAM