Asteroid Gravity-Field Estimation

1. Introduction

With the increasing interest in the Solar System's smaller bodies, quite a few missions have been sent to comets and asteroids, and more will be send in the near future. Due to the large distances involved, communication to command mission parameters takes a long time, which has a negative impact on operational safety. Autonomous navigation would be one of the key technologies that can make asteroid missions more robust, safe, and cost effective. This is especially true if one considers the unknown flight environment when the spacecraft is first encountering the body. Most asteroids and comets have a very irregular shape and unknown mass distribution. Therefore, knowledge about its irregular gravity field will be directly beneficial as input to orbital corrections and manoeuvre planning.

 

2. Methodology

Based on a detailed ``real-world'' simulator, orbits around a small body, here the asteroid Eros-433,  can be simulated that are perturbed by non-linear gravity effects, as well as solar-radiation pressure and third-body perturbations. Measuring land marks on the small-body's surface, processed (in a preliminary mission phase with Earth in the loop) to a detailed land-mark database, can be subsequently used to determine the (relative) position and velocity of the spacecraft with respect to the body. A next step would be to use measurements of orbital perturbations to estimate as many components of the body's gravity field as possible. Detailed knowledge about the gravity field can then be used for planning science and mission operations, such as orbital corrections. An in-house code is used to determine the spherical-harmonics coefficients C_nm and S_nm, assuming an average asteroid density of 2.6212 g/cm³.

 

Part of the navigation system are simplified sensors, which provide noisy position and/or velocity measurements. Interfacing with more realistic sensors is possible, but left as future work. The core of the navigation system is an augmented state estimator, based on the unscented Kalman filter for its applicability to highly non-linear systems.

 

3. Results

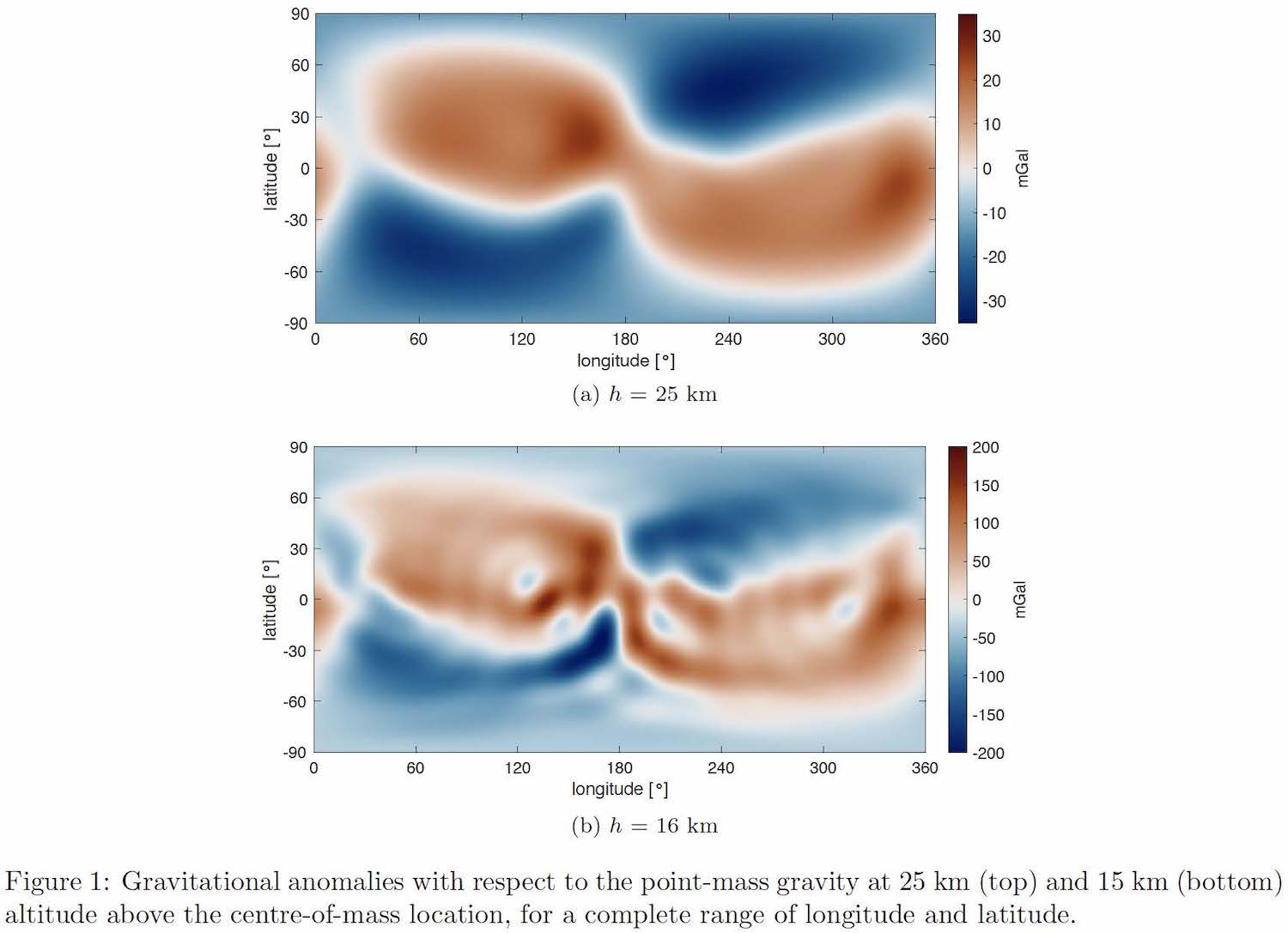
Eros-433 is an elongated body, roughly resembling an ellipsoid, with dimensions of 33 by 13 by 13 km, and rotates with an approximate constant rate in 5.27 hours. For the ``real-world'' asteroid model, a gravity field up to order and degree 16 has been determined, see Figure 1. The results shown are the deviations from the point-mass model and thus highlighting the irregularities of Eros' gravity field. With increasing altitude these irregularities are much more ``smeared out'' and will thus be harder to estimate.

 

 

The first simulations that were done aimed at estimating the central-field parameter, μ, and the first zonal harmonic, J₂ = C_2,0. To do so, several orbital altitudes ranging from 1500 down to 150 km were chosen. In terms of measurements data, it was assumed that only noisy position and velocity data were available at a frequency of 1 Hz. Figure 2 shows the estimates of μ. The remaining error is well below 0.1% for the different altitudes. With the estimated value of μ substituted in the filter, the estimate of J₂ is seen to converge best at an altitude of 45 km: at higher altitudes the J₂ effect starts to decrease and becomes less noticeable, whereas at lower altitudes the effect of the higher-order terms start dominating. The remaining error is about 6%.

 

 

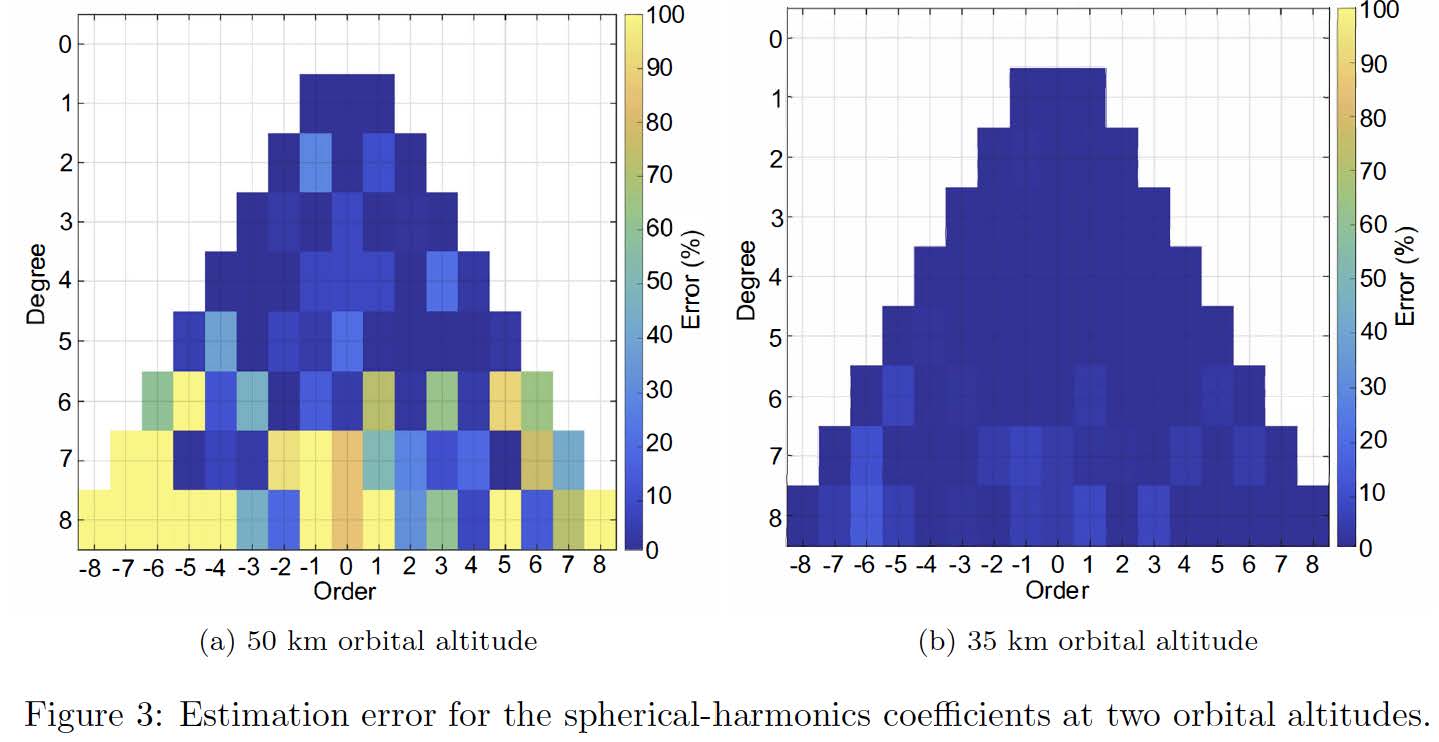
The last part of the research focusses on the estimation of higher-order coefficients. Idealised noisy position (noise level 10 m, which would be possible with current sensor technology) and velocity measurements are used, supported by ideal range measurements at 2 Hz. Figure 3a displays the errors of the full 8 degree and order coefficients for the estimation at an orbital height of 50 km. The coefficients of degree 6 and higher have significant errors, but the coefficients up to degree and order 5 can be estimated within errors of less than 30%. However, once μ and J₂ have been estimated and subsequently put to constant values in the estimator, the estimation accuracy significantly improves, but only when the orbit is lowered to 35 km and the measurement time is extended to 10 days (Figure 3b). The average error is about 10%, with a few outliers. These errors are quite small, because of the relatively ideal measurements. Follow-on research should therefore focus on realistic sensor modelling and including instrument errors to the augmented state.