Comparing Methods for Gravitational Computation: Studying the Effect of Inhomogeneities

Introduction 

Current and future small body missions, such as the ESA Hera mission [1] or the JAXA MMX mission [2] demand good knowledge of the gravitational field of the targeted celestial bodies. This is not only motivated to ensure the precise spacecraft operations around the body, but likewise important for landing manoeuvres, surface (rover) operations, and science, including surface gravimetry [3]. To model the gravitation of irregularly-shaped, non-spherical bodies, different methods exist. Previous work performed a comparison between three different methods [4], considering a homogeneous density distribution inside the body. In this work, the comparison is continued, by introducing a first inhomogeneity inside the body. For this, the same three methods, being the polyhedral method [5] and two different mascon methods [6][7] are compared. We will describe the methods and our test cases in the next Section. 

Methodology 

The polyhedral method (PM) provides an analytical solution to the gravitational potential field of any polyhedral body [5]. Intrinsically, the method demands a homogeneous density throughout the body, making it not directly applicable to account for inhomogeneities. Therefore, in this work, we perform a superposition of the gravitational fields of the main body and the inhomogeneities, considering the differential density, which can also be negative.  

The other two methods are based on mascons, namely MSP (Mascons: Sphere Packing) and MASC (Mascons: Spherical Coordinates). These mascon methods subdivide a body into smaller parts. The mass is then concentrated in the centre of these parts and the gravitational field is the sum of the individual accelerations. MSP uses a sphere packing with non-uniform-sized spheres that do not overlap (see Fig.1). Since the sphere packing does not cover the complete volume, we use additionally a heuristic that tends to assign smaller spheres more mass. To model inhomogeneity, we compute separate sphere packings with different densities assumed. With MASC, the internal mass distribution is modelled by dividing the body in longitude, latitude, and radius, and by assigning individual densities to the resulting set of tesseroids.  

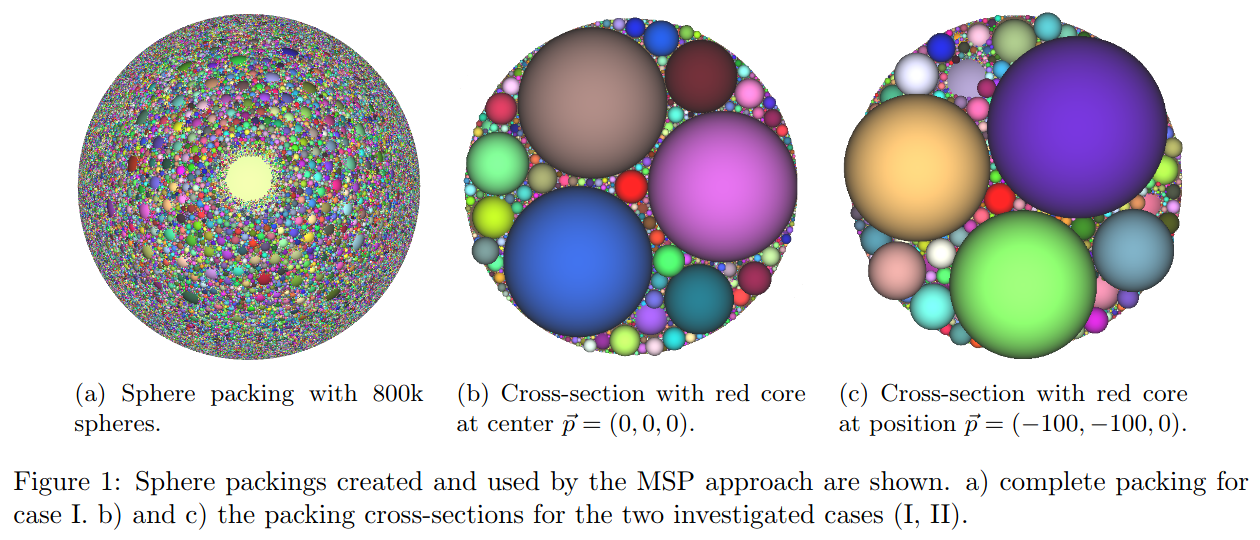
Test Cases  

Our two test cases consider two nested ideal spheres that are approximated through a UV-Sphere with 328,328 facets [4]. The outer sphere has a radius r=1,000 m and a density of 1.0g/cm³, and the inner sphere has a radius r=100 m and a density of 0.5g/cm³. In Case I, the inner sphere is placed concentric to the outer sphere, whereas in Case II the sphere’s centre is translated to X=−100 m and Y=−100 m. We compute the gravitational acceleration for points on the ideal sphere and compare it to the analytical solution through a relative error. Clearly, the ratio of computed and analytical solution τ =g_com /g_ana should always be <100% as the UV-sphere is only an approximation of the perfect sphere, values >100% represent an overshoot. This agreement ratio is presented in the next Section. 

 

First Results 

The overall results and range of τ on the surface of the sphere are summarized in Table 1:  

 

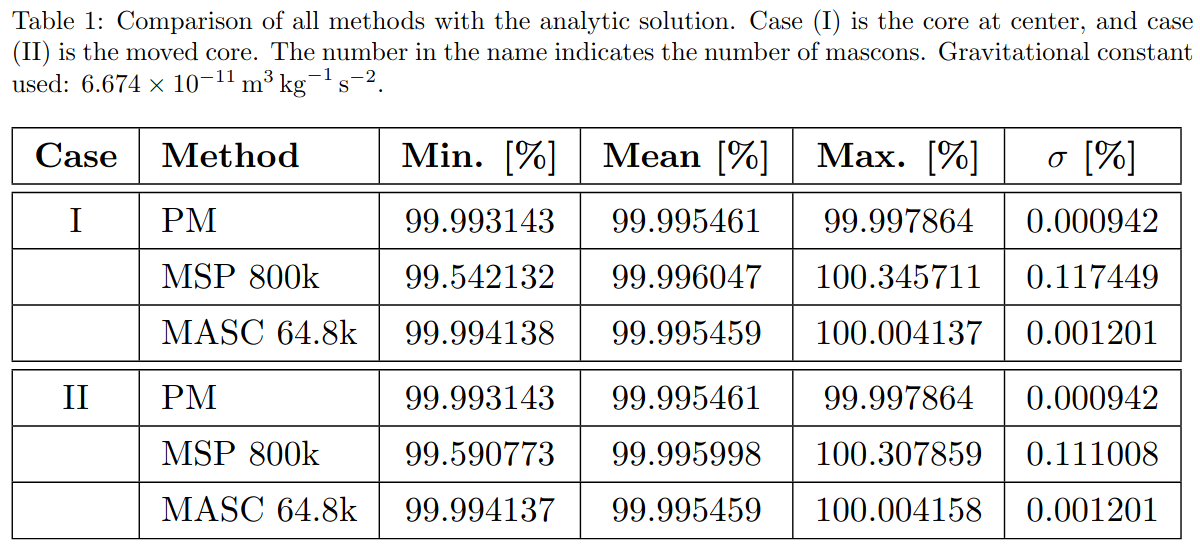
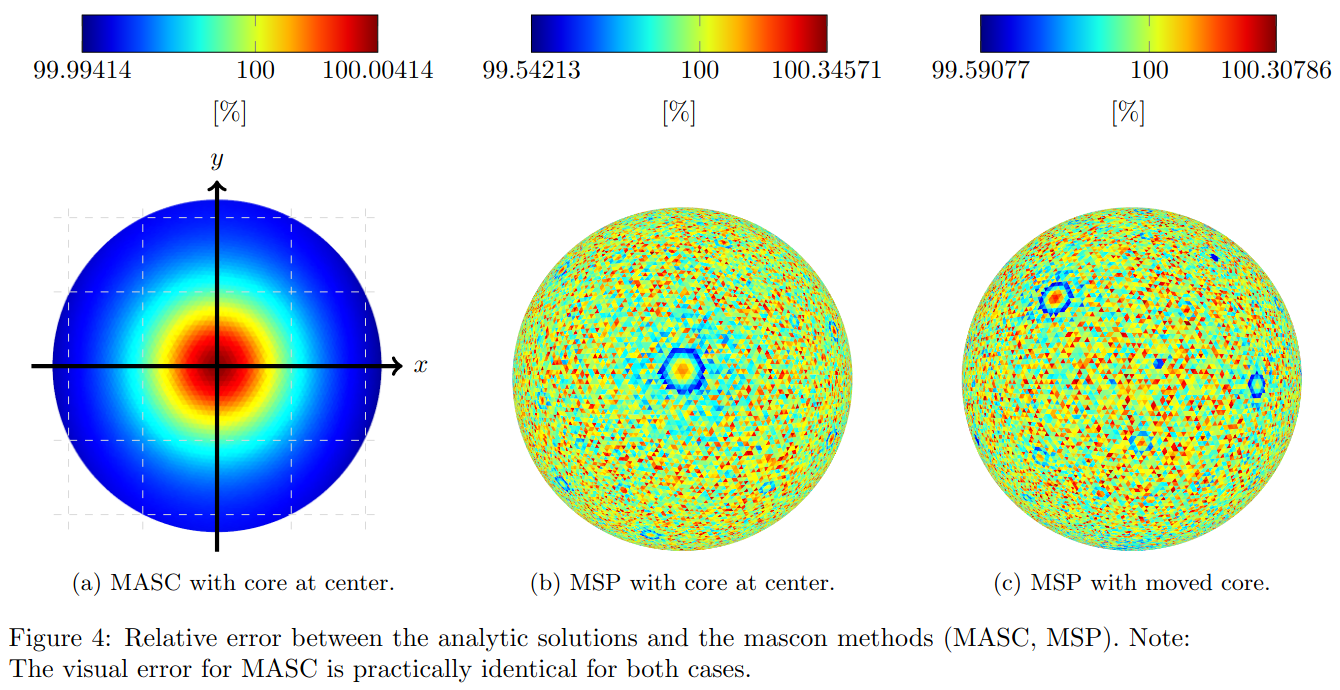
For both of our cases, PM delivers the most accurate results (Table 1). The error results from the shape approximation. It is visualized in Figures 1 and 2. We can see the expected shift from an almost equal to an unequal surface gravity. In Figure 1 we can also see that the shape approximation error is larger than the floating-point precision limitation (noisy pattern, Figure 1a). 

 

 

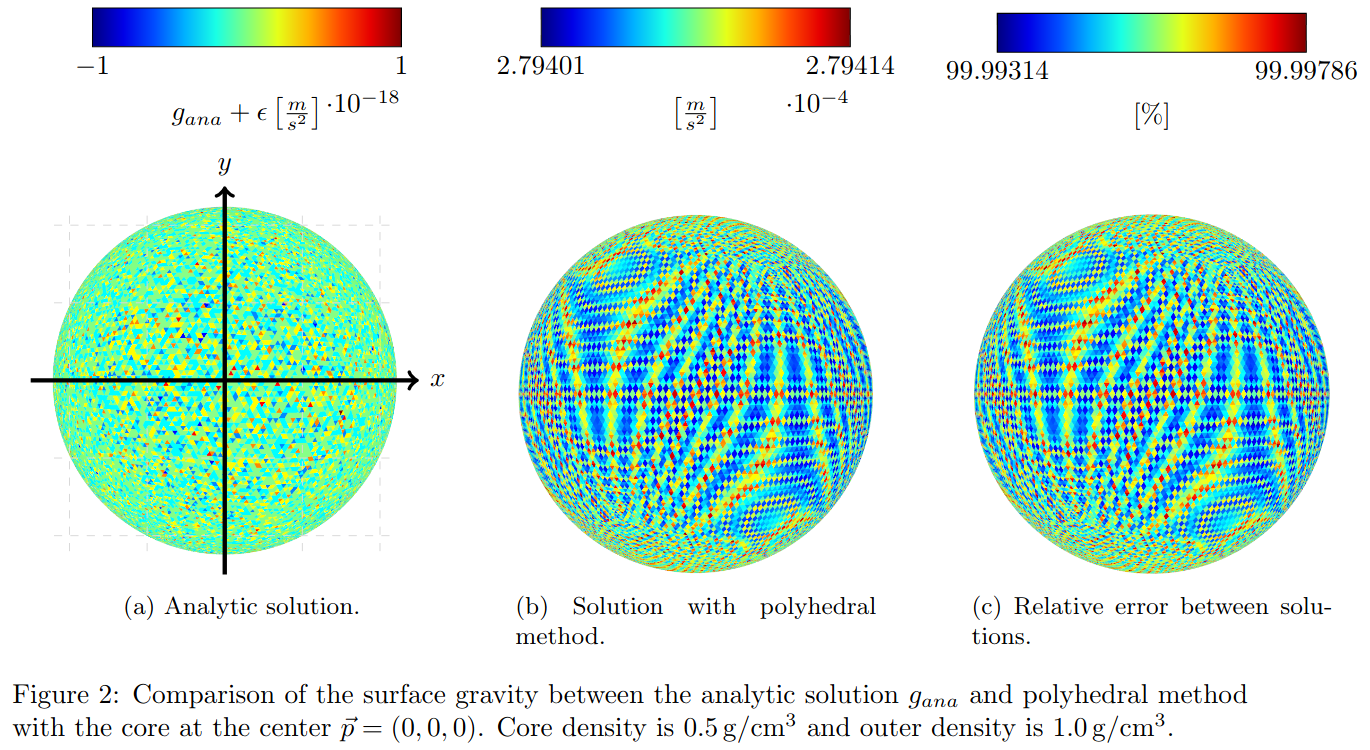
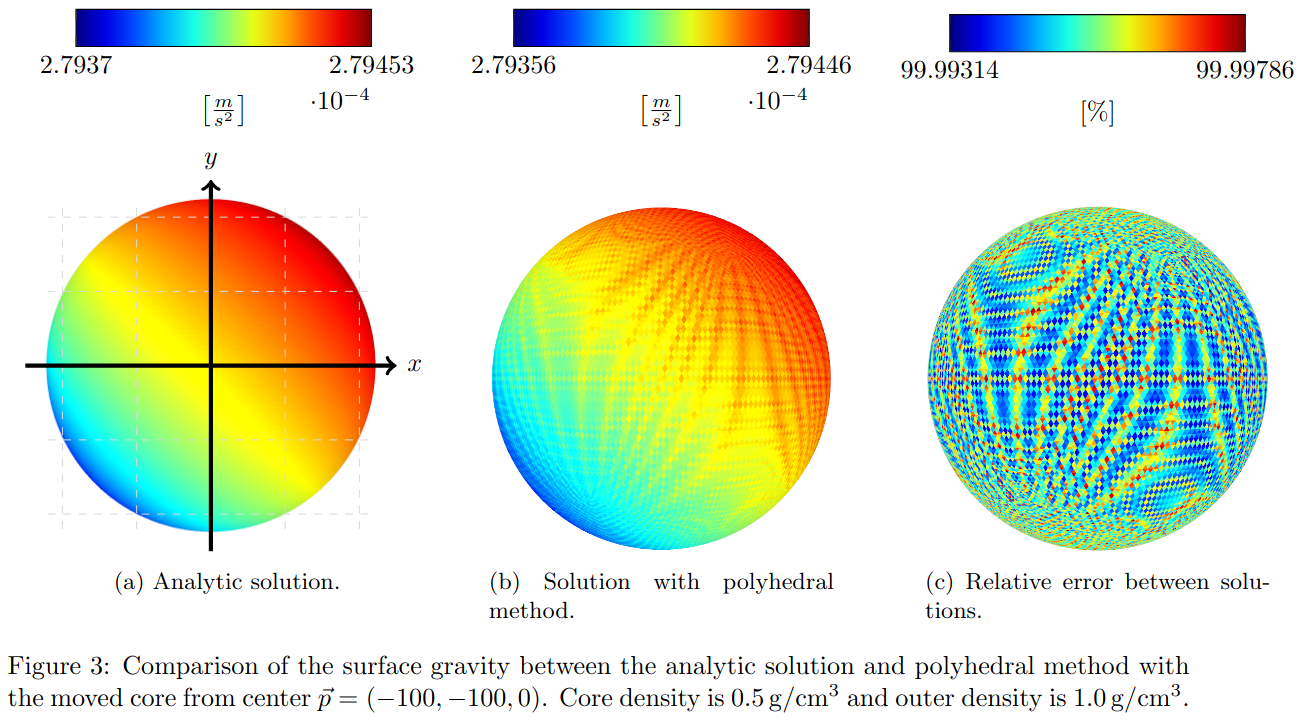
The MSP method creates a noisy overshooting pattern (see Figures 4b and 4c), which results from the spheres near the surface and the heuristic. Large spheres lead to a circular artifact at the surface. Observable at the center of Figures 4b and 1a. It is a similar pattern for Case II. The MASC error results from the subdivision in spherical coordinates. At the poles the number of tesseroids increases, which leads to a circular overshoot at two sides. It is also true for the shifted core (see Figure 4a). The computation time for MSP remained the same as for the homogeneous case [4] while it has doubled for PM and MASC. 

 

The three methods presented above for the computation of the gravitational acceleration will be applied to more complex shapes for irregularly shaped bodies. In addition, different inhomogeneous density distributions representing the interior will be studied and the according results presented.     

Acknowledgements 

M.N. acknowledges funding from the Foundation of German Business (sdw) and the Royal Observatory of Belgium (ROB) PhD grants. The work by Bundeswehr University was carried out in the frame of project KaNaRiA-NaKoRa which is funded by DLR under grant FKZ50NA1915. The work on the part of University of Bremen presented in this paper was partially funded by DLR under grant 50NA1916. 

References 

[1] Michel, Patrick, et al. "The Hera mission: European component of the ESA-NASA AIDA mission to a binary asteroid." 42nd COSPAR Scientific Assembly 42 (2018):B1-1. 

[2] Campagnola, Stefano, et al. "Mission analysis for the Martian Moons Explorer (MMX) mission." Acta Astronautica 146 (2018):409-417. 

[3] Noeker, Matthias, et al. "The GRASS Gravimeter Rotation Mechanism for ESA Hera Mission On-Board Juventas Deep Space CubeSat." Proceedings of the 46th Aerospace Mechanisms Symposium, Virtual, May 11-13, (2022):159-172. 

[4] Meißenhelter, Hermann, et al. "Efficient and Accurate Methods for Computing the Gravitational Field of Irregular-Shaped Bodies." 2022 IEEE Aerospace Conference. IEEE, 2022. 

[5] Werner and Scheeres. "Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia." Celestial Mechanics and Dynamical Astronomy 65.3 (1996):313-344. 

[6] A. Srinivas, et. al. “Fast and accurate simulation of gravitational field of irregular-shaped bodies using polydisperse sphere packings.” in ICAT-EGVE, 2017, pp.213–220. 

[7] M. Pätzold, et. al. “Phobos mass determination from the very close flyby of Mars Express in 2010,” Icarus, vol. 229, pp. 92–98, Feb.2014.