Numerical modeling of thermal wave in layered icy surface

Introduction:

The properties of icy surfaces in the Solar System evolve under the effect of numerous processes either external, internal or induced by the climate. Thanks to spaceborne remote sensing data, we have access to the current microphysical and compositional state of ices (see for instance Cruz Mermy et al 2022, EPSC [1]) but quantifying the numerous mechanisms involved remains challenging. To study these surfaces hard to access, our goal is to build a one-dimensional numerical model of planetary ices evolving over time.

This task consists in creating an unprecedented innovative tool general to many icy surfaces in the solar system, similar to what the SNOWPACK model does for Earth snow evolution (Tuzet et al., 2017 [2]). These simulations would predict ice microphysics within a depth of a few meters evolving on multiple seasons. They will integrate multiple physical processes (heat transfers, phase changes, surface energy balance, ice grains metamorphism and spatial weathering) acting on the ice layers and couple them with each other.

The numerical scheme will be designed to be versatile enough to activate/deactivate each physical process parametrization. When possible, several approximations of each process will be designed in order to better control numerical efficiency versus realism. Several pieces are already present in the literature, but the novelty and extremely promising nature of the present approach is to encompass them all, since they all contribute to the evolution of ices with potentially similar time and length scales.

We would like to present the thermic module which gives the evolution of the temperature profile of the ice for different layers of variable properties. Previous models have been designed to estimate the thermal transfer in the subsurface, such as LMD 1D (Forget et al, 1999 [3]), KRC (Kieffer et al., 2013 [4]), THERMPROJRS (Spencer et al. 1989 [5]). Among them, some have been designed to model Earth snow evolution, such as SNTHERM (Jordan, 1991 [6]) and SNOWPACK (Tuzet et al., 2017 [2]). Here, we propose to follow the standard heat equation but solve it numerically for non-constant heat properties, especially with time and depth dependent thermal inertia.

 

Methods:

In this model, the boundary condition is given by the energy equilibrium at the surface: the incoming absorbed solar flux is balanced by the black body emission and the heat flux from the ground. The thermic properties of the materials can be depth and time dependent. We have discretized the heat equation in these conditions and solved the system of equations with an implicit solver.

The spatial grid representing space is discretized as a vector which starts at the planet’s surface and ends such that the zero-flux condition at the bottom is respected. In terms of time discretization, we run the algorithm several sideral days, with a thousand timesteps each. The aim is to validate the algorithm by comparing with analytical and standard numerical solutions.

 

Results

Validation of our algorithm by comparison with well-known analytic solutions of the heat equation is possible in specific conditions. For a material of constant conductivity, density and heat capacity, the one-dimensional heat equation can be solved analytically for a given set of initial and boundary conditions. In particular, for an initial step function profile bounded in a box with no flux at the boundaries, the solution can be expressed as a Fourier Series which is obtained through separation of variables. Results show a perfect fit between the numerical and analytical solutions which proves that our model works well for a material with constant properties (see figure 1).

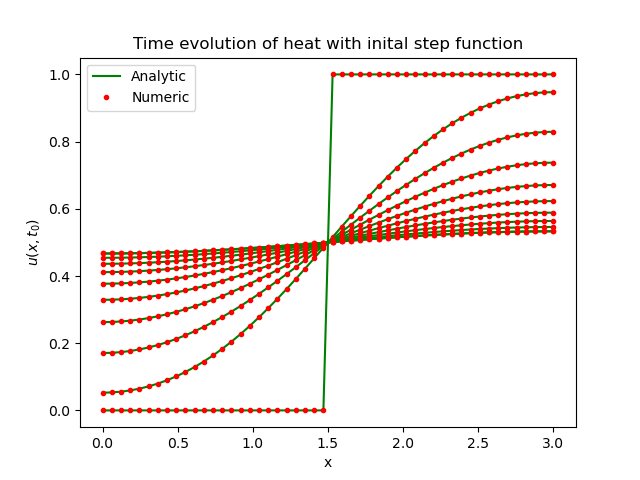
Figure 1:  Comparative evolution of the temperature profiles.

 

In more complex cases, in particular when the heat conductivity is depth dependent, analytical solutions of the heat equation do not exist. In these cases, validation of the model comes from comparison with experimental data or from other previously well-established numerical algorithms. Here we choose to compare our method with Spencer’s explicit algorithm for realistic planetary surface conditions (Spencer et al. 1989).

To compare these two models, one must make sure that the initial conditions are the same. Notably, the solar flux responsible for the temperature evolution must be equal. In this fairly simple insolation model Spencer chose to approximate the heating of a planet surface by the Sun throughout a sidereal day by a sinusoidal function. The resulting total surface flux is the equilibrium between the solar flux and the surface black body emission. Results show that the two flux are identical (see figure 2).

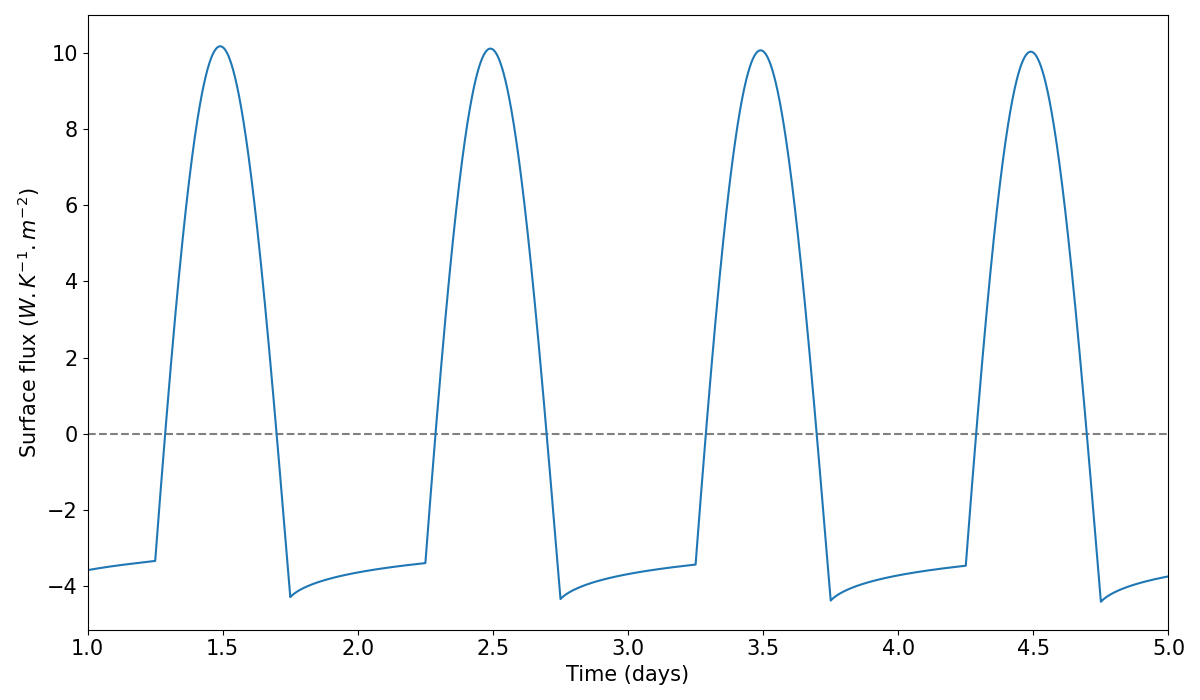
Figure 2: Evolution of the surface flux during multiple days (Blue).

 

For the sake of validation, values of density, heat capacity and conductivity were varied as a function of depth by the largest scales allowed by Spencer’s explicit scheme stability criteria (see figure 3).

Figure 3: Depth dependant properties profiles.

These results show that our implicit model is fully compatible with Spencer’s explicit algorithm, without the restrictions of stability (see figure 4). Using an implicit model will greatly help us to choose our own set of parameters.

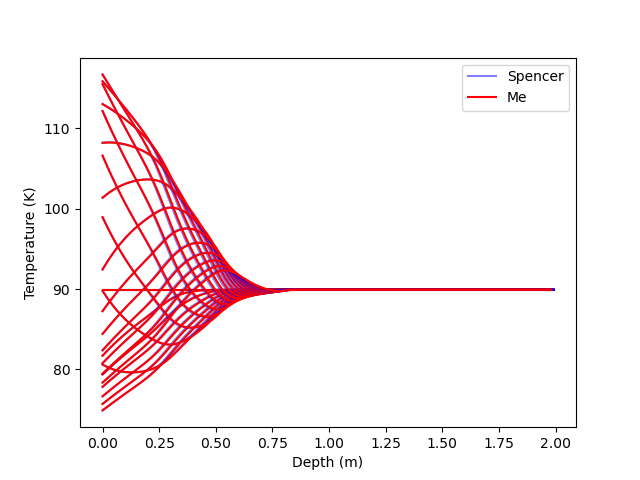
Figure 4: Comparative evolution of Spencer’s temperature profile (Blue
lines), and our implicit scheme temperature profiles (Red lines).

 

Conclusion and Perspectives

We implemented an implicit numerical scheme in Python to solve the heat transfer equation in a layered medium. It has been validated by comparison with analytical solutions and a reference numerical implementation. Our implicit scheme solver of the heat equation has the advantage of ensuring stability and convergence regardless of the material’s properties.

Now we plan to extend our simulation by coupling other processes acting on ice microphysics like ice grains metamorphism. We also plan to use this algorithm to retrieve surface properties in infrared and radar wavelength.

 

References:

[1] Cruz-Mermy et al., 2022, EPSC 2022

[2] Tuzet et al., 2017, The Cryosphere, 11

[3] Forget et al, 1999, JGR, 104

[4] Kieffer et al., 2013, JGR, 118

[5] Spencer et al. 1989, Icarus, 78

[6] Jordan, 1991, Documentation SNTHERM, 89