Mercury and OrbFit packages for numerical orbit propagation: Implementation of the Yarkovsky and YORP effects

Introduction:

The dynamics of Solar System objects is determined by their mutual gravitational interactions. In addition, non-gravitational effects need to be taken into account to properly model the dynamics of objects smaller than about 30-40 km in diameter. For asteroids, two the most relevant effects are the Yarkovsky and Yarkovsky-O’Keefe-Radzievskii-Paddack (YORP). The Yarkovsky effect is caused by sunlight. When an asteroid is heated up by the Sun it eventually re-radiates the energy away as heat, creating a tiny thrust. This recoil acceleration is much weaker than the gravitational forces, but it can produce substantial orbital changes over long timescales. The same physical phenomenon is also responsible for the YORP effect, a thermal torque that, complemented by a torque produced by scattered sunlight, can modify the rotation rates and obliquities of small bodies as well (e.g. Bottke et al. 2006, Vokrouhlický et al. 2015). Therefore, the Yarkovsky effect changes the orbital motion of an asteroid, while the YORP effect changes its spin state. However, as the magnitude of the Yarkovsky effect depends on the spin state, the two effects are coupled. For this reason, a high-precision analysis of the orbit evolution of small objects requires both effects to be considered.

N-body integrators for small solar system objects:

The three most widely used numerical integration packages in the planetary science community are swift (Levison and Duncan 1994), mercury (Chambers and Migliorini 1997), and orbit9 (Milani and Nobili 1988) which is included in the OrbFit package. In addition to these well-established packages, rebound (Rein and Liu 2012) became a top-rated tool in the last few years. The last decade also saw a fast improvement in the performance of graphical processing units (GPUs). GPUs can efficiently handle parallel computing, and for this reason, packages such as Genga (Grimm and Stadel 2014) have been developed to exploit the advantages of this kind of hardware.

For studies of the long-term evolution of small Solar System objects, it is fundamental to add the Yarkovsky and YORP effects to the dynamical model. Implementations of these effects in publicly available N-body codes, however, are typically lacking or the effects are implemented using simplified models. In this work, we describe the implementation of the Yarkovsky/YORP effect in the mercury and orbit9 integrators (Fenucci and Novakovic 2022). Both integrators have been extensively used for simulations of the long-term orbit evolution of asteroids.

Mercury and Orbit9: implementation of Yarkovsky and YORP effects:

To implement the two effects in the mercury and orbit9 integrators we adopted the following strategy. The Yarkovsky effect is computed as a non-conservative vector field along the tangential direction that produces the semi-major axis drift given by analytical theories (e.g. Vokrouhlický 1999). For the YORP effect, we follow an approach similar to the one described in Bottke et al. (2015), which is suitable for statistical studies of the evolution of asteroids. In our code, we provide two different YORP models: a static and a stochastic one. Along with the two effects, we introduced the effect of collisions and breakups on the asteroid spin state.

Results:

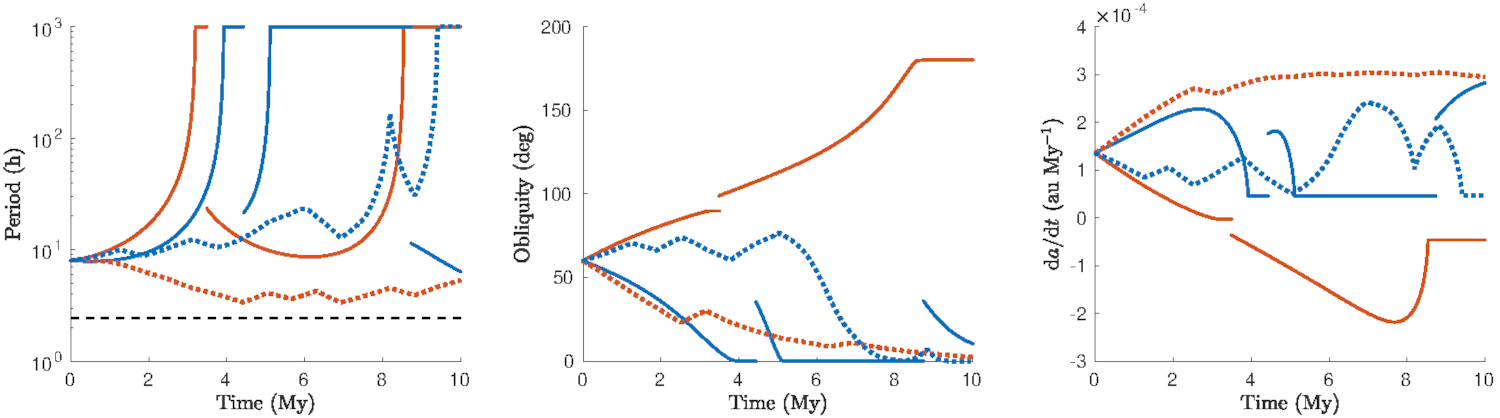
An example of the results obtained with the new versions is shown in Figure 1. The figure shows the evolution of an asteroid's spin period, obliquity, and semi-major axis drift for different integrators and YORP models. The red colour corresponds to the mercury integrator, while the blue represents the orbit9 integrator. The solid curves depict the simulations performed with the static YORP model, while dotted curves are those from the stochastic YORP model.

Repositories:

The new versions of the integrators that allow for proper treatment of the non-gravitational forces are publicly available at https://github.com/Fenu24/mercury (Mercury package), and at https://github.com/Fenu24/OrbFit (Orbit9 integrator).

References:

• Bottke, William F., J., Vokrouhlický, D., Rubincam, D. P. and Nesvorný, D. 2006, AREPS, 34, 157

• Bottke, W. F., Vokrouhlický, D., Walsh, K. J., et al. 2015, Icarus, 247, 191

• Chambers, J. E. and Migliorini, F. 1997, in AAS/DPS Meeting Abstracts #29, AAS/Division for Planetary Sciences Meeting Abstracts, 27.06

• Fenucci, M., Novakovic, B. 2022, Serb. Astron. J. 204, 51–63

• Grimm, S. L. and Stadel, J. G. 2014, ApJ, 796, 23

• Levison, H. F. and Duncan, M. J. 1994, Icarus, 108, 18

• Milani, A. and Nobili, A. M. 1988, Celestial Mechanics, 43, 1

• Rein, H. and Liu, S. F. 2012, A&A, 537, A128

• Vokrouhlický, D., Bottke, W. F., Chesley, S. R., Scheeres, D. J. and Statler, T. S. 2015, The Yarkovsky and YORP Effects (University of Arizona Press), 509–532