Study of convection in high-pressure ice layers of large icy moons and implications for habitability

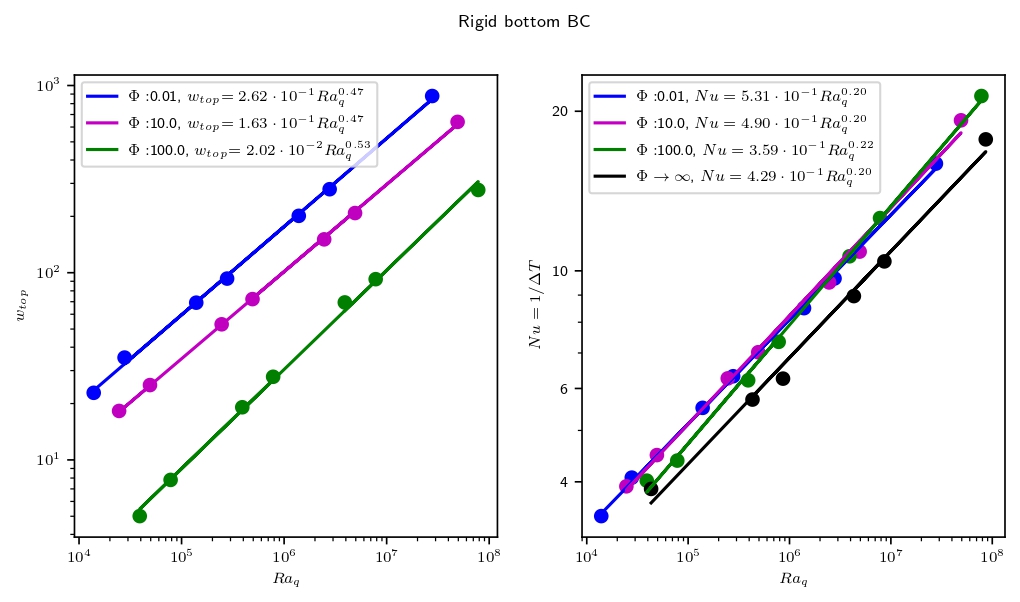
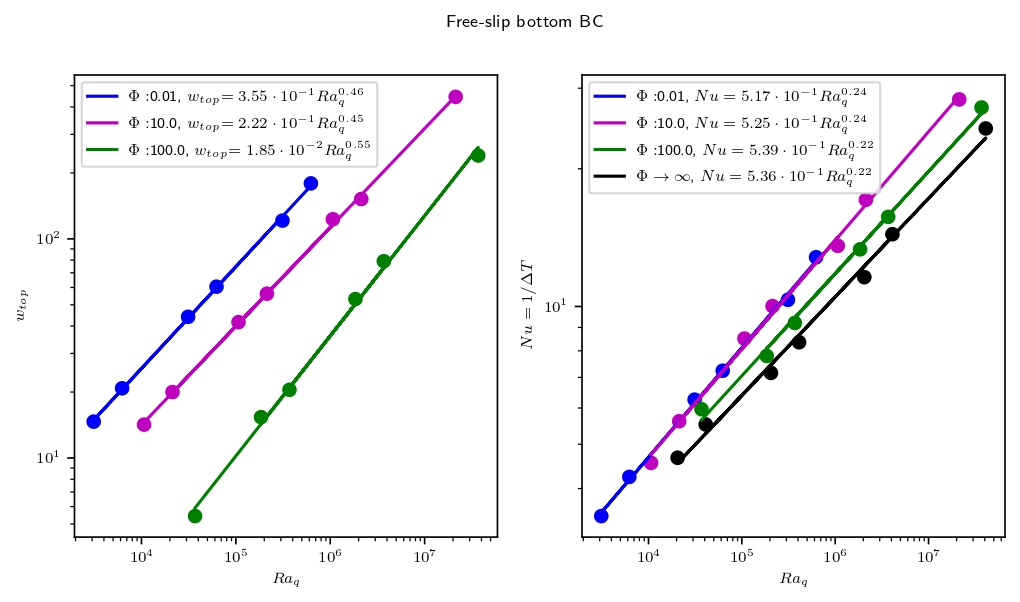
The existence of a high-pressure (HP) ice layer between the silicate core and the liquid ocean in large icy moons and ocean worlds is usually seen as a barrier to habitability, preventing a direct contact and therefore transfer of nutrients from the core to the liquid ocean (Figure 1). More recently, several studies [1-3] challenged that hypothesis and showed that exchanges were possible under specific conditions, allowing transport of salts toward the ocean. In the first part of our study, we considered an effect not taken into account in the previous works, which is the dynamical implications of the phase equilibrium at the ice-ocean interface allowing a non-zero vertical velocity at the surface of the HP ice layer. Convective stresses in the solid create a topography of the interface which can be erased by melting and freezing if flow on the liquid side is efficient. This effect, which can be modeled as a phase change boundary condition for the ice layer, has a significant impact on the flow dynamics and enables exchanges with the ocean by fusion and crystallization at the top interface of the HP ice layer, even without partial melting in the bulk of the ice layer [4]. For the same conditions as standard convective systems, it also leads to faster mass transfer in the bulk [5]. These exchanges are directly linked to the melting capacity of the ice at the interface between the HP ice layer and the core, depending on the efficiency of convection in the liquid ocean and quantified by a unique parameter, Φ. Considering this boundary condition at the interface between the HP ice layer and the liquid ocean, we propose a scaling of the bottom temperature and the top vertical velocity as function of the Rayleigh number (Figure 2), in the case of a fixed heat flux from the core, a rigid or free-slip bottom boundary and various values of the phase change parameter, Φ (Figure 1).

 

In the interest of separating the problems, we first started with a model that does not include partial melting and compositional variations. But, in the case where the heat flux from the core would be sufficient to reach the melting temperature at the boundary between the core and the HP ice layer, and because the temperature at the interface is laterally variable, a thin film of melt, or localized melt pockets, could exist along the bottom of the ice shell. This melt, containing salts from the core, could be transported into the ocean through the ascending hot plumes into the HP ice layer by successive melting and refreezing episodes. Then, we performed preliminary calculations based on the results of this first study, applied to Ganymede, and the conclusion is that in several conditions melt occurs at the bottom boundary and even in the bulk of the HP ice layer. Then, the partial melting and two-phase convection into the HP ice layer will be considered in further studies.

 

The second part of this study is to include impurities into the HP ice layer in order to study the ability of salt transfer by convection in the solid. Salts can enter the ice layer by diffusion, a very inefficient process. Otherwise, if melting occurs at the bottom of the ice layer, as mentioned above, liquid water can get enriched in salt and, since water is lighter than high pressure ice, it can rise by porous flow or fracking and refreeze. This results in a high concentration of salts in a layer of ice some height above the bottom boundary. This ice is denser than pure ice at the same temperature and can impede convection depending on the ratio of density increase associated to salts compared to the decrease associated to temperature, a ratio called buoyancy number Bi. We study this problem using Lagrangian tracers in the convection code and adding a flux of salts in a layer at the bottom of the ice layer. We study the effects of the buoyancy number on the heat and salt transfer efficiency in the layer, and the implications for the evolution of salt concentration in the ocean.

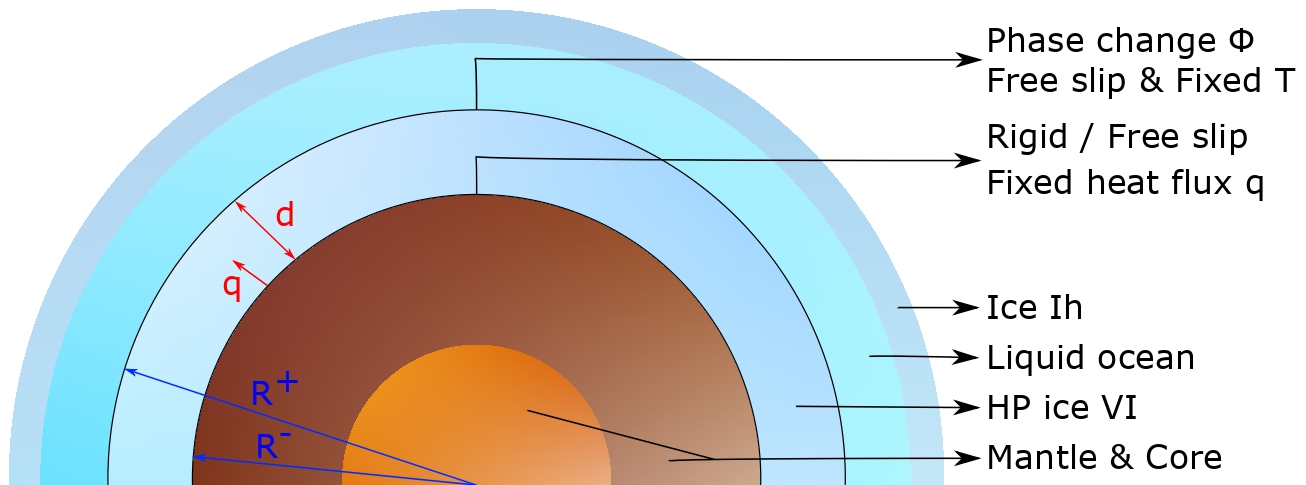
Figure 1 - Model illustration for the interior of an ocean world with an HP ice layer.

Figure 2 - Left panel shows the dimensionless radial velocity at the top boundary of the HP ice layer. Right panel shows the dimensionless Nusselt number. Both in function of the Rayleigh Number and for various values of Φ.

 

References:

[1] G. Choblet, G. Tobie, C. Sotin, K. Kalousová, O. Grasset (2017). Heat transport in the high-pressure ice mantle of large icy moons. Icarus, 285, 252-262

[2] K. Kalousová, C. Sotin, G. Choblet, G. Tobie, O. Grasset (2018). Two-phase convection in Ganymede’s high-pressure ice layer — Implications for its geological evolution. Icarus, 299, 133-147

[3] K.Kalousová, C. Sotin (2018). Melting in High-Pressure Ice Layers of Large Ocean Worlds—Implications for Volatiles Transport. Geophys. Res. Lett., 45, 8096-8103.

[4] Labrosse, S., Morison, A., Deguen, R., & Alboussière, T. (2018). Rayleigh–Bénard convection in a creeping solid with melting and freezing at either or both its horizontal boundaries. J. Fluid Mech., 846, 5–36. https://doi.org/10.1017/jfm.2018.258

[5] Agrusta, R., Morison, A., Labrosse, S., Deguen, R., Alboussière, T., Tackley, P. J., & Dubuffet, F. (2020). Mantle convection interacting with magma oceans. Geophys. J. Int, 220, 1878–1892. https://doi.org/10.1093/gji/ggz549