FFT gravity field calculation method and super-ellipsoid generated field

Introduction

In the frame of the H2020 NEO-MAPP project, we are studying the problem of determining the detailed gravitational field of an arbitrary body as a strategy to get information about the internal structure of irregular shaped and non-homogenous small solar system objects, like asteroids. Our reference asteroid is the Near-Earth Asteroid (65803) Didymos binary system, the target of the Hera mission by the European Space Agency [1] to be launched in late 2024.

We propose an extremely fast Fast Fourier Transform (FFT) [2] based method to find the gravitational field in all regions of space about any body with any shape and mass distribution, with particular attention on Didymos. This has the advantage of calculating -in a reasonable time- the gravitational fields corresponding to a large number of extremely different internal structures. Therefore, on the one hand we will be able to test the suitable resolution needed for accelerometers onboard Hera’s Juventas cubesat [3]. On the other hand, once the Hera spacecraft will be at Didymos, measurements may be compared with a comprehensive library of potential gravitational fields. In that way, we may find what synthetic internal structure best matches spacecraft measurements. As a complementary strategy to our FFT based method, we explore a super-ellipsoidal geometry that provides a route to compute analytically an approximation of the gravity field assuming homogeneous bodies.

Methodology

Our FFT based method starts by considering a primary three-dimensional cartesian grid that has uniform point spacing in the directions parallel to the x, y and z axes and contains the mass density ρ(r) that characterizes the considered body. The density ρ(r) is then discretized at each primary grid points, thus characterizing the mass distribution of the body, which creates the gravity field. Next, our algorithm considers a secondary three-dimensional cartesian grid that applies an arbitrary translation to the primary one and represents the space region where the gravity field will be computed. Once the primary and secondary grids have been defined, our algorithm computes efficiently the components of the gravity vector created by the body within the primary grid at all the secondary grid points.

Our algorithm has been applied to bodies having regular and irregular shapes as well as uniform and non-uniform densities, and its high accuracy has been tested by comparison with other exact analytical or numerical solutions. Using 16 GB of RAM memory in different PCs, we achieve primary and secondary grids of up to 241 points at each axis and computation times that do not exceed one minute for each secondary grid. In the case of Didymos, the computed gravity field provided by our algorithm has been compared with the exact analytical results for homogeneous polyhedral shape models, showing a very good agreement between both methods. In addition, we have explored a super-ellipsoidal geometry that provides a route to compute analytically the gravity field created by the homogeneous polyhedral Didymos shape model with a very good accuracy except at points which are very near the surface.

Results

For the Near-Earth Asteroid (65803) Didymos we consider the polyhedral shape model depicted in figure 1, which is made up 1996 triangular facets assuming a uniform density of 2170 kg/m³. Such density has been discretized by considering 241 cells in the x, y and z axes while imposing the condition that the density at each cell ensures a correct total mass at such cell.

The resulting discretized density at the equatorial plane is depicted in figure 2 (a), whereas the computed gravity field modulus with our FFT based method (at the equatorial plane) is shown in figure 2 (b). Figure 2 (c) shows the relative error between the computed gravity field modulus in figure 2 (b) and the exact analytical gravity field modulus for the considered polyhedral shape model [4]. It can be observed that the relative error is always below 0.65 % reaching only such value in very few points on the surface.

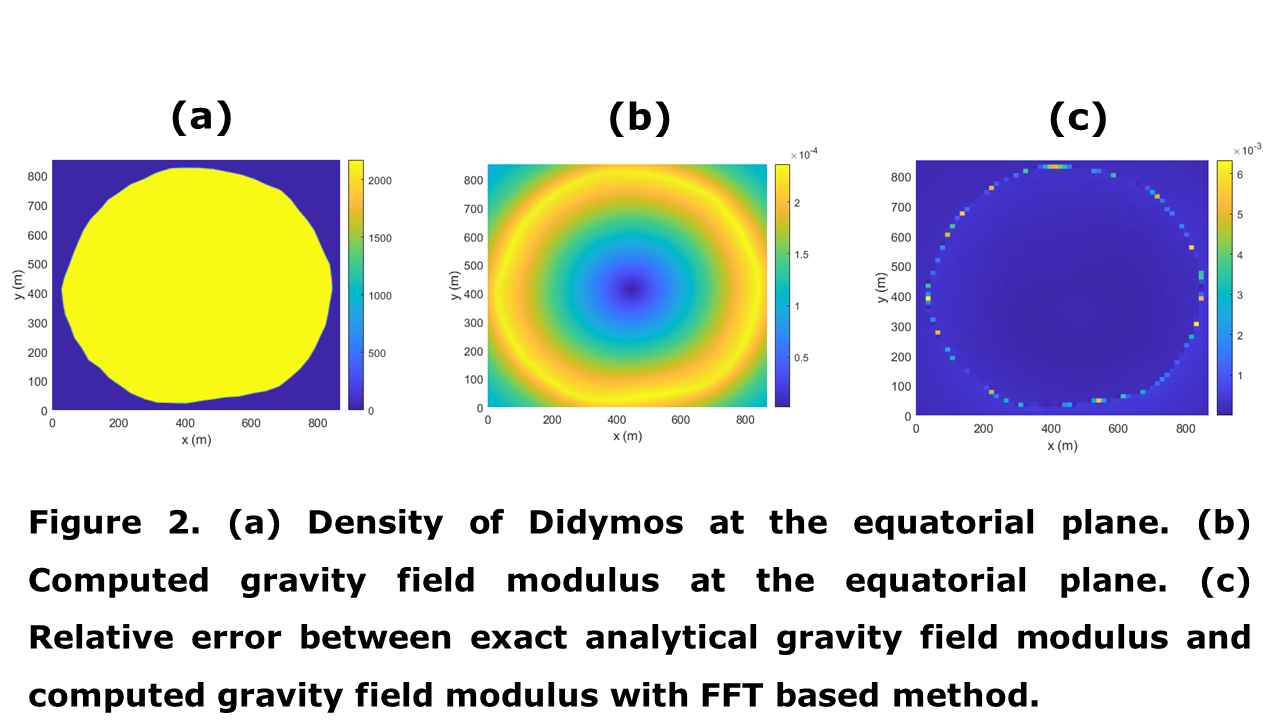
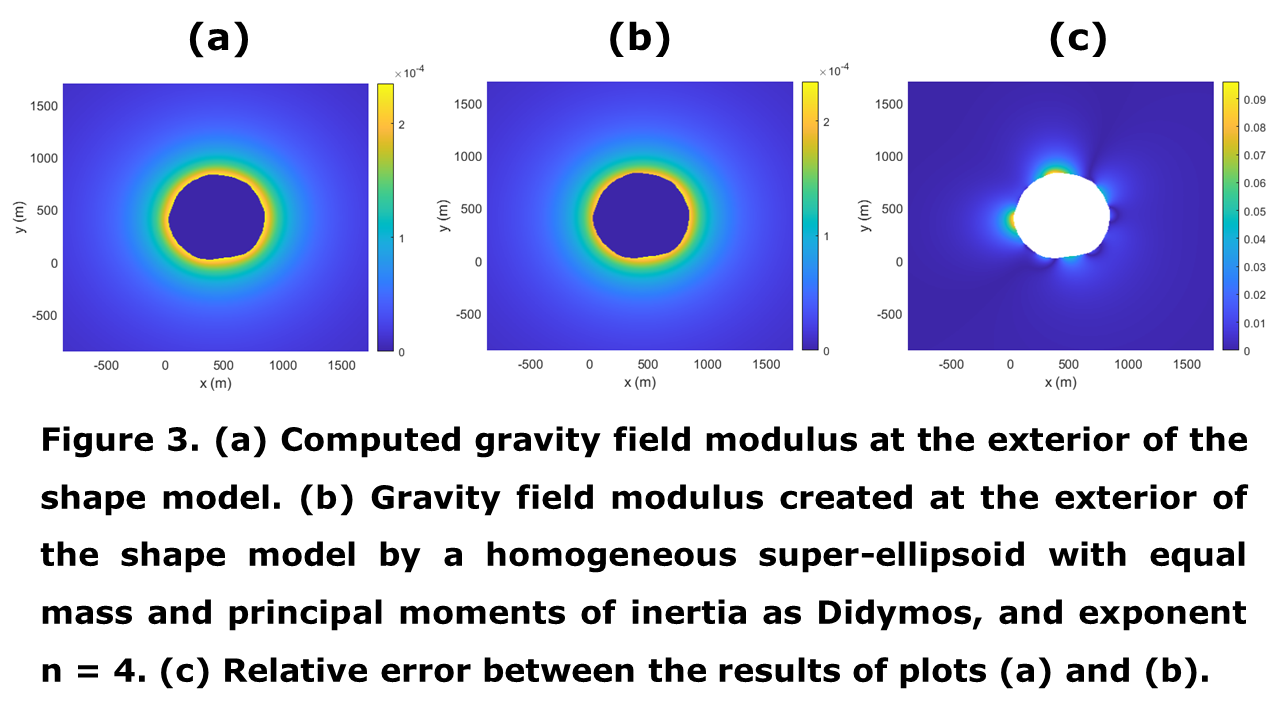
Figure 3 (a) shows the computed gravity field modulus for the considered polyhedral shape model in an extended outer region of Didymos at the equatorial plane by using our FFT based method, for which we have considered 9 independent secondary grids covering such region. Figure 3 (b) shows the gravity field modulus created at the same points by a homogeneous super-ellipsoid [5] with exponent n = 4 having the same mass and principal moments of inertia as Didymos shape model, and with its principal central axes coinciding with those of Didymos. It can be observed that there is a good agreement between the results of figures 3 (a) and 3 (b) except at points very near the surface of Didymos. This is corroborated in figure 3 (c), which depicts the relative deviation between the results of figures 3 (a) and 3 (b).

References

[1] Michel, P. et al. (2018) Adv. in Space Res. 62, 2261-2272.

[2] Cooley, J. W., Tukey, J. W. (1965) Math Comp. 19, 297-301.

[3] Goldberg, H., Karatekin, O. (2019) 21st EGU General Assembly, EGU2019. id.16735

[4] Werner, R. A. (1994) Celest. Mech. Dyn. Astron. 59, 253-278.

[5] B. Y. Ni, I. Elishakoff, C. Jiang, C. M. Fu, X. Han. (2016) Appl. Math. Mod. 40, 9427-9444.