OPS6
Session assets
Discussion on Slack
Orals: Thu, 22 Sep | Room Andalucia 2
Many observations have been made in recent years of the visible/near-IR spectra of the Giant Planets: Jupiter, Saturn, Uranus and Neptune (Fig. 1). Spectroscopic observations in reflected sunlight are complemented by studies of aerosol opacity at thermal wavelengths, from 5 µm into the mid- and far-infrared. Observations in reflected sunlight can be inverted to infer vertical atmospheric structure using retrievals algorithms such as NEMESIS. In this paper, we will review recent observations and compare and contrast the aerosol structures derived to be present in these planetary atmospheres. Common themes that will be explored are:
- Cloud condensation requires cloud condensation nuclei (CCN), small particles that can ‘seed’ the condensation process. Such materials are common in Earth’s atmosphere, blown up from the surface or ocean, but to understand formation in Ice Giant atmospheres, which have no surface, we are reliant on photochemistry in the upper atmosphere to photolyse gases such as ammonia and methane to generate hydrocarbon and nitrile hazes. This has a strong effect on where clouds/hazes can form.
- These photochemically-produced hazes are significantly absorbing at some wavelengths, which affects the observed colours of these planets and also how the reflectance varies with solar and observing zenith angle, i.e., limb-darkening.
- Moist convection on the giant planets is very different from that in the Earth’s atmosphere. Moist air in the Earth’s atmosphere is naturally buoyant since water vapour has a lower molecular weight than the surrounding N2/O2 air. On giant planets, however, moist air containing ammonia, water vapour or methane, has a significantly higher molecular weight than the surrounding H2/He air and hence tends to sink. Precipitation of condensed phases of ices, such as ammonia-water ‘mushballs’ on Jupiter, can be responsible for changing the vertical distributions of condensable species considerably, compared to equilibrium condensation models.
- Regions of cloud condensation can lead to a significant decrease of mean molecular weight with height, leading to regions of significant static stability that may help suppress convection, and potentially separate atmospheric circulation into multiple stacked layers of differing properties.
While reviewing these recent measurement and retrieval studies we will also outline how degenerate the solutions are: since we have very little prior knowledge and limited data there are a wide range of solutions that can fit the observations equally well. Fortunately, we have found that the Minnaert limb-darkening model gives us a means of reducing this degeneracy and we shall show how this approach has greatly improved the robustness and reliability of our recent retrievals.
Figure 1. Visible appearance of the giant planets in our solar system: Jupiter (upper-left), Saturn (upper-right), Uranus (lower-left) and Neptune (lower-right)
How to cite: Irwin, P., Teanby, N., Fletcher, L., Toledo, D., Orton, G., Wong, M., Roman, M., Pérez-Hoyos, S., Sanz Raquena, J. F., James, A., Alexander, C., and Dobinson, J.: Aerosols in the atmospheres of the Giant Planets, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-197, https://doi.org/10.5194/epsc2022-197, 2022.
1 - Introduction
In the atmosphere of the satellite Titan, the photochemistry of its two main components N2 and CH4 leads to the formation of complex organic molecules, up to the production of solid aerosols, in the form of an orange haze. Observations from the Cassini-Huygens mission [1], as well as models [2] and laboratory experiments [3], strongly suspect that once formed in the ionosphere, the haze will reside for some time in Titan's atmosphere until settling on the surface. Our aim is to investigate experimentally the interaction of the haze particles with their atmospheric chemical environment, focusing on possible reactive molecules produced by gas phase photochemistry of N2 and CH4 such as HCN, HC3N, C2N2, C2H2, C2H6. We more specifically addressed the absorption processes of the gases on the particle (uptake coefficients).
2 - Experimental method
In this experimental study, a dusty plasma reactor is used to simulate the atmospheric chemistry of Titan [3], as well as the synthesis of Titan’s aerosols analogues (tholins). The gaseous precursors formed by electronic dissociation were monitored in-situ by mass spectrometry, simultaneously with the formation and growth of the haze particles. The properties of the tholins are analyzed by scanning electron microscopy (morphology and size) and high resolution mass spectrometry, LDI-FTICR (chemical composition). In this study, the injection gas flow rate was optimized in order to increase as much as possible the residence time of the gas mixture in the reactor. The chemical growth of the solid particles is thus favored, allowing to follow simultaneously the formation and the evolution of the particles, as well as the co-evolution of the composition of the gas mixture until reaching a stationary gas chemistry, which will not change any more during the whole experiment.
3- Results
3.1 - Temporal evolution of the gas phase by mass spectrometry
In a previous study [4], MID monitoring by mass spectrometry was performed for CH4 and HCN (Figure 1). From these results, we distinguish two kinetic regimes of gas-particle interaction: a transient regime corresponding to the production and consumption of gases and correlated to the evolution of tholins solid particles, and a stationary regime where the gas mixture ratio is stabilized. In this study, the MID monitoring is carried out for gas-phase molecules suspected to participate to the tholins chemical growth (so called “precursors”) : C2H2, C2H6, HC3N, C2N2.
Figure 1 - Time evolution of the masses m/z 16 (CH4), 27 (HCN), obtained with a mass spectrometer [4].
3.2 - Microphysical evolution by scanning electron microscopy
The samples were observed by scanning electron microscopy. The images show two growth phases, each corresponding to a gas-particle kinetic regime distinguished by the MID monitoring. Tholins during the transient regime exhibit nanoscale spherical monomers, not exceeding ~200 nm in diameter (Figure 2.A). Tholins formed in the stationary regime show an evolution of spherical monomers up to diameters of a few µm, and the formation of aggregates (Figure 2.B et 2.C).
Figure 2- Morphologies of Titan's tholins obtained with SEM. Figure 2.A : Tholins formed during the transient regime have an average diameter of 200 nm. Figure 2.B : Evolution of spherical nanometric to micrometric particles. Figure 2.C : Tholins formed during the strationnary regime, have an average diameter of a few µm.
3.3 - Kinetic modeling of the gas-particle interaction
Based on a kinetic model performed by Pöschl et al. in 2007 [5], the two kinetic regimes observed in the experiment are fitted. From it, the absorption coefficient γ (uptake coefficient) of Titan tholins was deduced for each monitored precursor.. For each regime, an absorption coefficient γ is calculated taking into account the different interactions between gas-surface of the particles, as well as between surface-bulk of the particles, i.e. adsorption, desorption and diffusion effects.
[1] : Israël G. et al., Nature 438 : 796-99 (2005).
[2] : Lavvas P. et al., The Astrophysical Journal (2011).
[3] : Szopa C. et al., Planetary and Space Science 54 (2006).
[4] : Perrin et al. Processes, MDPI (2021)
[5] : Pöschl U. et al., Atmospheric Chemistry and Physics 7 (2007)
How to cite: Perrin, Z., Carrasco, N., Ruscassier, N., Maillard, J., Schmitz Afonso, I., Drant, T., Vettier, L., and Cernogora, G.: Heterogeneous chemistry on Titan : Evolution of Titan’s tholins through time with gas phase chemistry, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-448, https://doi.org/10.5194/epsc2022-448, 2022.
- Introduction
The Saturn system has been explored for 13 years (2004-2017) by the Cassini-Huygens mission that revealed the extraordinary chemical diversity of Titan and Enceladus. In particular, O+ ions (1 - 100 keV), originating from Enceladus' geysers, precipitate in Titan's upper atmosphere where molecules reaching mass-on-charge (m/z) of several thousand atomic mass units have been detected. These aerosol embryos have been attributed to polycyclic aromatic (nitrogen bearing) hydrocarbons (PANHs) that most likely result from the ionization and dissociation of the major atmospheric compounds, N2 and CH4 by solar photons [Hörst, 2017]. It is to be expected that the small fraction of energetic O+ ions, implanting themselves in organic aerosols, would modify their optical properties and chemical composition. If complex oxygenated molecules are formed, the aerosols, by sedimenting towards the surface, can then provide it with prebiotic material, adding a dimension with strong exobiological implications to the carbon / nitrogen / hydrogen chemistry endogenous to Titan [Hörst et al., 2012]. The objective of this project is thus to study the impact of oxygen ions from 1 to 100 keV on Titan aerosol analogues (tholins) and model materials by characterizing their effect on the chemical, structural and optical properties of the targets.
- Experimental Methodology
Preliminary experiments were performed with adenine samples. Adenine was chosen because (i) it is a PANH, (ii) it has been identified in Titan’s tholins [Hörst et al. 2012; Sebree et al., 2018], (iii) there is some existing literature on its irradiation by UV photons and ions over a wide energy range showing that it does form a solid residue probably of macromolecular nature [Gerakines et al. 2012; Vignoli Muniz et al. 2017; Poch et al. 2014], (iv) some protocols to deposit it as a thin film on windows were available at LISA [Poch et al. 2014; Saïagh et al. 2014]. The samples consist of a thin (150 – 500 nm) adenine deposit on a MgF2 or ZnSe window. 8 samples were irradiated in the IGLIAS set-up at the ARIBE beam line at GANIL (Caen, France) with 35 or 70 keV 17O4+, 18O5+, or 20Ne3,4+ at a total fluence ranging from 9x1014 to 5x1015 ions cm-2. Samples were kept at 300 or 150 K and under ultra-high vacuum. Using the Stopping and Ranges of Ions in Matter (SRIM) software, we calculated that ions stop at a depth of 100 and 200 nm, for 35 and 70 keV incident ions, respectively, ensuring that they are implanted well within the sample. IR absorption spectra were obtained in situ during the irradiation with a Brüker V70 FTIR spectrometer.
- Results and Conclusions
During energetic ion irradiation of the adenine films, their overall IR absorption intensity decreases (Fig. 1). The adenine molecule disappearance is caused by both destruction and sputtering. The projected stopping range being lower than the sample thickness, a part of the sample is not irradiated and the evolution of a given peak area A as a function of the ion fluence F can be written as
A(F) = a*exp(-bF)+Y*F+c,
where a is the initial absorption of the peak area, b is the destruction cross section, Y characterizes the sputtering yield and c gives the number of molecules in the non-irradiated layer at the end of the experiment.
Figure 1: Infrared absorption spectra of adenine at 300 K under irradiation of 35 keV 18O5+ at different fluences.
Table 1 displays the destruction cross section and sputtering yield (v7, 1609 cm-1) for different projectiles and temperatures. Our destruction cross sections are similar to that obtained for 1 keV and 0.8 MeV H+ [Gerakines et al. 2012; Vignoli Muniz et al. 2017]. The sputtering yield often has a large error but a rough approximation is that 15% to 35% of the sample is sputtered away. Further experiments with in situ mass spectrometry measurements of the gas phase could determine whether the sputtered material is intact adenine or some other molecules. Samples irradiated at 150 K have the largest destruction cross section and sputtering yield. This behavior has also been observed in previous experiments performed in the MeV range where the decay rate increased with decreasing temperature [Gerakines et al. 2012; Vignoli Muniz et al. 2017].
|
Projectile |
T |
b |
Y |
|
35 keV 18O5+ |
300 |
(1.71±0.08)e-15 |
6±1 |
|
35 keV 18O5+ |
150 |
(3.6±0.9)e-15 |
11±26 |
|
35 keV 20Ne3+ |
300 |
(2.5±0.1)e-15 |
13±1 |
Table 1: Destruction cross section (cm2) and sputtering yield (molecules/ion) for different projectiles and temperatures (K).
Beyond adenine destruction, a new broad IR absorption band clearly arises between 2050 and 2250 cm-1 that may be attributed to nitriles or isonitriles. However, we could not find any evidence for absorption bands from oxygen-bearing molecules. More sensitive ex situ analysis of the irradiated samples by mass spectrometry are ongoing to characterize the macromolecular residue.
Acknowledgements
We thank the Programme National de Planétologie (PNP) for supporting this work.
References
Gerakines, P.A. et al. « In situ measurements of the radiation stability of amino acids at 15–140 K ». Icarus 220, 647 (2012).
Hörst, S. M. et al. Formation of amino acids and nucleotide bases in a Titan atmosphere simulation experiment ». Astrobiology 12, 809 (2012).
Hörst, S. M. « Titan’s atmosphere and climate ». J. Geophys. Res. Planets 122 (2017): doi:10.1002/2016JE005240.
Poch, O. « Laboratory insights into the chemical and kinetic evolution of several organic molecules under simulated Mars surface UV radiation conditions ». Icarus 242, 50 (2014).
Saïagh, K. « VUV and mid-UV photoabsorption cross sections of thin films of adenine: Application on its photochemistry in the solar system ». Planet. Space Sci. 90, 90 (2014).
Sebree, J. A. et al. « Detection of prebiotic molecules in plasma and photochemical aerosol analogs using GC/MS/MS techniques ». ApJ 865, 133 (2018).
Vignoli Muniz, G. S. et al. « Radioresistance of adenine to cosmic rays ». Astrobiology 17, 298 (2017).
How to cite: Shouse, J., Launois, T., Chaouche, N., Wolters, C., Boduch, P., Quirico, E., Stalport, F., Flandinet, L., Orthous-Daunay, F.-R., Cottin, H., and Vuitton, V.: Exploring in the Laboratory the Impact of Low Energy Oxygen Ions on Titan’s Aerosols, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-246, https://doi.org/10.5194/epsc2022-246, 2022.
The complexity of the phenomena taking place in exoplanet atmospheres is challenging to simulate and choices have to be done to simplify the problem. The choice of using a one dimensional atmospheric model is potentially the most resource-saving one, though when considering effects of transport, a new caveat appear: how to account for such 3D-related processes in 1D ? The answer is: considering all these complex phenomena as a single diffusion process called eddy diffusion (Colegrove et al., 1965; Smith, 1998; Moses et al., 2011; Lavvas & Koskinen, 2017). This is a long known simplification, yet no complete theoretical frameworks exist to accurately assess this parameter and most 1D models assume either a constant eddy diffusion coefficient treated as a fitting parameter (Spiegel et al., 2009), or a profile derived from 3D general circulation models (Parmentier et al., 2013; Zhang & Showman, 2018). Unfortunately, all planets haven’t been studied with such a model and therefore, no accurate eddy profile derived from GCMs can be found for these planets. Moreover, the different ways to derive the eddy via 3D model provide very different results. In this work, we aim to develop a parametrization suitable for gas giant exoplanets and to assess the eddy profile obtained for ten hot-Jupiters.
We developed an eddy profile parametrization based on parameters available in 1D calculations. The parameterization separates the atmosphere in three parts: a convection-driven mixing below the radiative-convective boundary (Ackerman & Marley, 2001), a middle atmosphere eddy diffusion increasing with decreasing density in a √1 behavior (Chamberlain, 1978), and an upper atmosphere above the homopause where we consider a constant eddy diffusion coefficient scaled on Jupiter’s homopause eddy mixing (Koskinen et al., 2010).
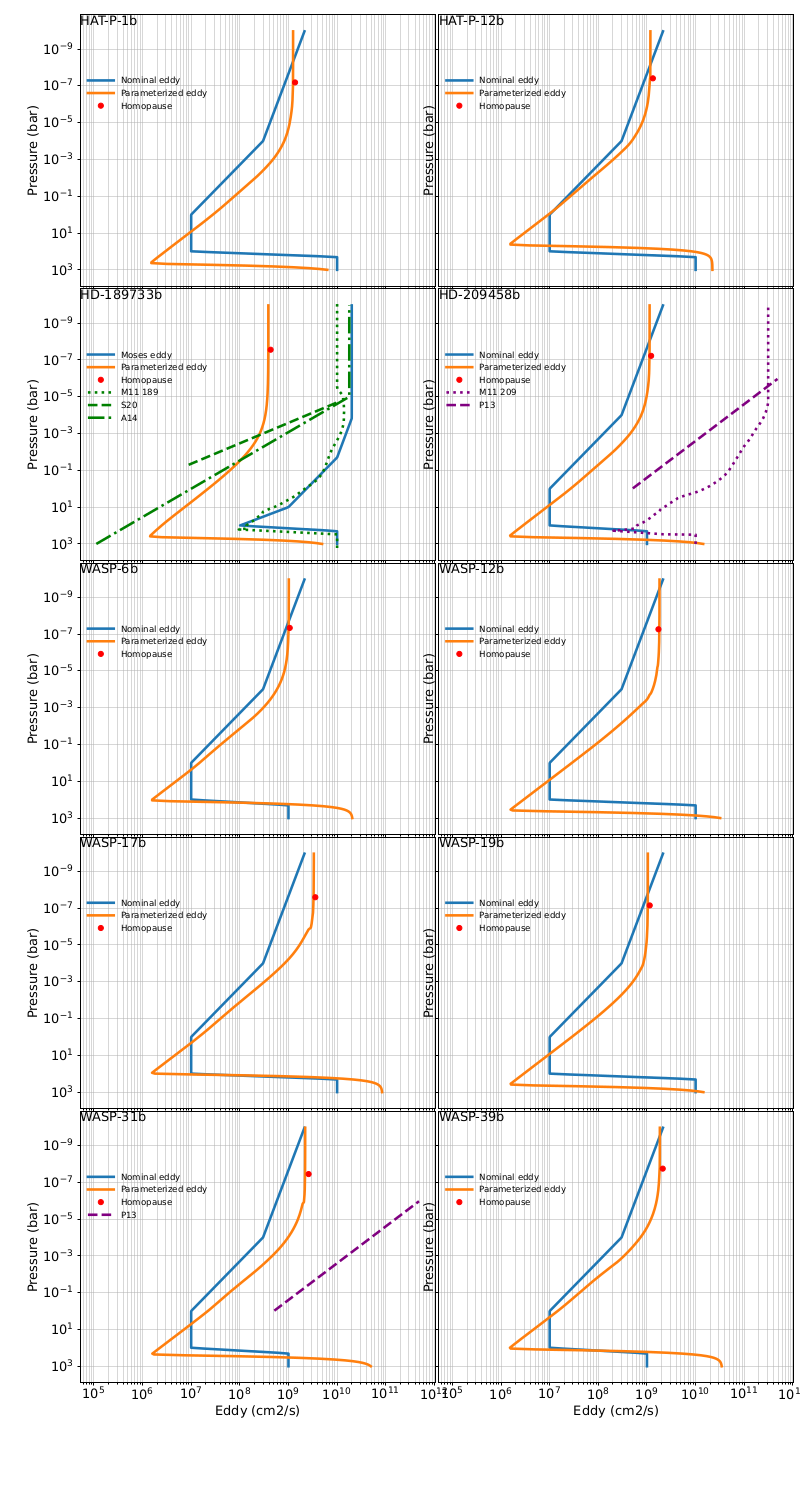
Figure 1: Nominal and parametrized eddy profiles. When available, additional GCM results are shown (M11 for Moses et al. (2011), S20 for Steinrueck et al. (2020), A14 for Agùndez et al. (2014), P13 for Parmentier et al. (2013)).
The eddy profile affects the transport and then the distribution of chemical species and hazes in the atmosphere, thus resulting in modifications of the transit spectra. Therefore, in the purpose of testing this parameterization, we use a self-consistent 1D model that couples haze microphysics (Lavvas & Koskinen, 2017), disequilibrium chemistry (Lavvas et al., 2014) and radiative transfer (Lavvas & Arfaux, 2021). We conducted two sets of calculations: the first with a nominal eddy profile based on the profile derived by Moses et al. (2011) for HD-189733b and downscaled following Parmentier et al. (2013) results, and the second with our parametrization (Fig. 1). The modification of the eddy can bring important modifications of the haze particle distribution with a stronger mixing leading to a decrease of the transport timescale. This produces smaller and more numerous particles as they have less time to coagulate. The changes in the haze particle distribution are impacting the transit spectra. While the spectra of haze-free atmospheres present weak variations from the nominal eddy case, the smaller particles obtained for hazy planets result in a significant decrease of the transit depth (Fig. 2). These planets would therefore require more haze to fit the HST observations. This result is consistent with the larger haze precursors mass fluxes we obtain. Indeed, modifying the eddy leads to important modifications of the chemical composition profiles, notably the haze precursors. The stronger upper atmosphere (usually in the region up to ∼0.01 μbar altitude as shown in Fig. 1) eddy mixing produced by our parametrization enhances HCN and CO abundances, which are considered to be the major contributors to the formation of photochemical hazes. This increases the production of hazes with precursors photolysis mass fluxes multiplied by 5 on average compared to the nominal eddy case.
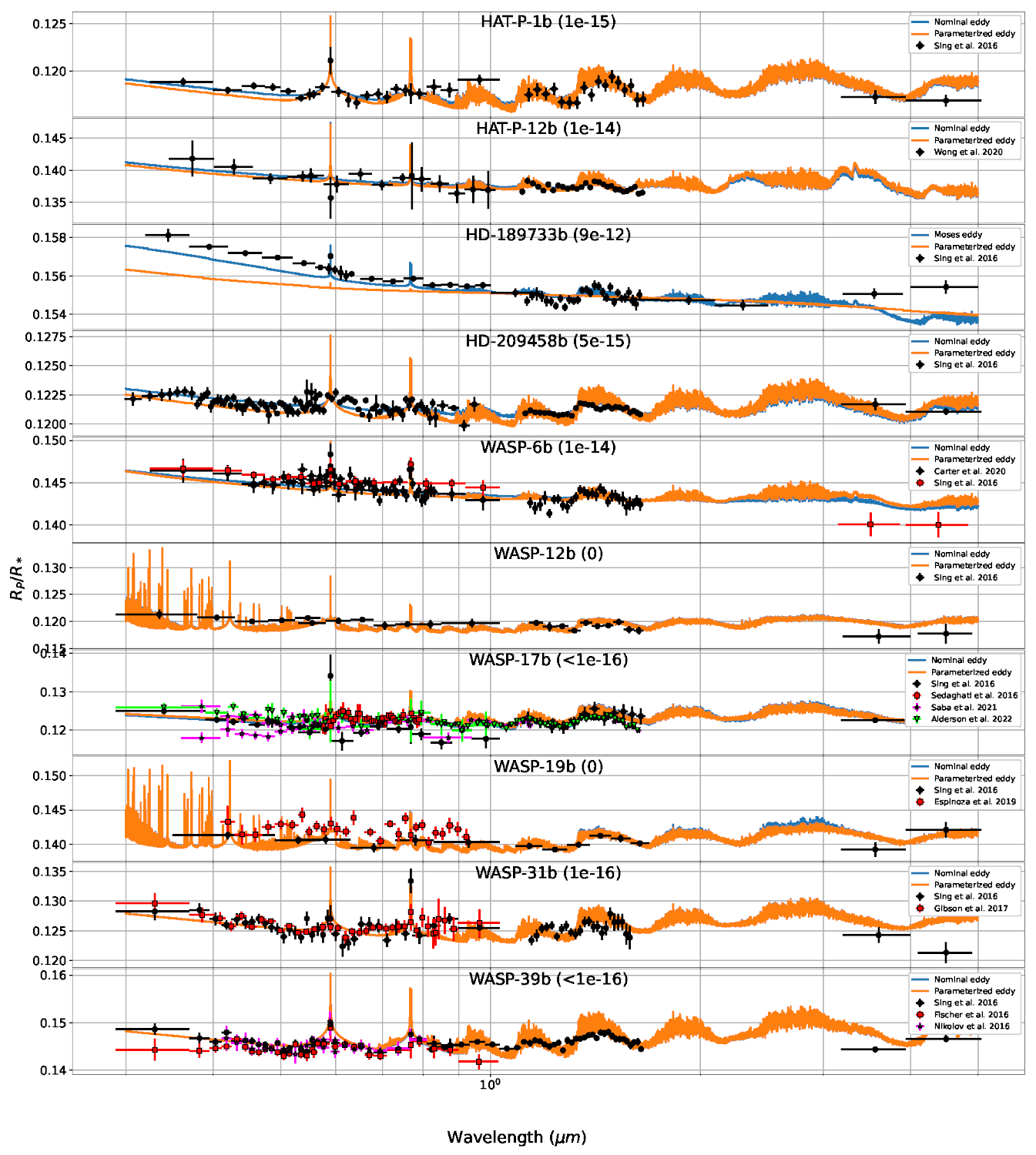Figure 2: Transit spectra obtained with the nominal and parametrized eddy profiles. The values in parentheses are the mass fluxes assumed for the haze formation in g.cm−2.s−1.
In conclusion, our parameterization produces in most cases eddy profiles rather close to the nominally used, mainly slightly larger in the upper atmosphere. These new eddy profiles require some slight adjustment of the haze mass flux to fit the observations compared to the mass fluxes derived using the nominal eddy profile. We however note the particular case of HD-189733b (Fig. 1). This planet indeed requires a particular care due to its challenging UV-visible observations (Fig. 2) that imply haze mass flux and eddy diffusion significantly larger than for the other planets.
References
Ackerman, A. S., & Marley, M. S. (2001). The Astrophysical Journal, 556(2), 872–884.
Agùndez, M., Parmentier, V., Venot, O., Hersant, F., & Selsis, F. (2014). Astronomy and Astrophysics, 564, A73.
Chamberlain, J. W. (1978).
Colegrove, F. D., Hanson, W. B., & Johnson, F. S. (1965). Journal of Geophysical Research, 70(19), 4931–4941.
Koskinen, T. T., Cho, J. Y.-K., Achilleos, N., & Aylward, A. D. (2010). The Astrophysical Journal, 722(1), 178–187.
Lavvas, P., & Arfaux, A. (2021). Monthly Notices of the Royal Astronomical Society, 502(4), 5643–5657.
Lavvas, P., & Koskinen, T. (2017). The Astronomical Journal, 847.
Lavvas, P., Koskinen, T., & Yelle, R. V. (2014). arXiv e-prints, (p. arXiv:1410.8102).
Moses, J. I., Visscher, J. J., C.; Fortney, Showman, A. P., Lewis, N. K., Griffith, C. A., Klippenstein, S. J., Shabram, M., Friedson, A. J., Marley, M. S., & Freedman, R. S. (2011). The Astrophysical Journal, 737(1).
Parmentier, V., Showman, A. P., & Lian, Y. (2013). Astronomie and Astrophysics, 558, A91.
Smith, e. a., M. D. (1998).
Spiegel, D. S., Silverio, K., & Burrows, A. (2009). The Astrophysical Journal, 699(2), 1487–1500.
Steinrueck, M. E., Showman, A. P., Lavvas, P., Koskinen, T., Tan, X., & Zhang, X. (2020). arXiv e-prints, (p. arXiv:2011.14022).
Zhang, X., & Showman, A. P. (2018). The Astrophysical Journal, 866(1), 1.
How to cite: Arfaux, A. and Lavvas, P.: Sensitivity of hot-Jupiter haze retrieval on eddy parameterization, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-328, https://doi.org/10.5194/epsc2022-328, 2022.
Posters: Thu, 22 Sep, 18:45–20:15 | Poster area Level 1
Abstract
We present Doppler wind velocity final results of Saturn’s zonal flow at cloud level. Our aim is help to constrain the characterization of the equatorial jet at cloud level and the latitudinal variation of the zonal winds, to measure its spatial and temporal variability, to contribute to monitor the variability in order to achieve a better understanding of the dynamics of Saturn’s zonal winds (Sánchez-Lavega et al. 2003, 2007, 2016); Finally, the complementarity with Cassini, providing an independent set of observations.
Figure 1: (a) Raw echellogramme showing the spectral orders for one of the detectors. (b) Magnification of part of one order, where absorption lines (dark vertical bands) are visible. From each order, a stack of 61 spectra are extracted. (c) Set of 61 spectra, with each one corresponding to one pixel in the slit’s active window. (d) Each spectrum is divided into 16 orders in the MIT detector and 23 orders in the EEV detector. The plot shows an example of the 16 components of an MIT spectrum, each coming from one spectral order. (e) Example spectrum from one order and one location in the Venus disk. Machado et al. (2012).
The study of the planet’s global system of winds at the 0.7 bar region is based on high resolution spectra from the UV-Visual Echelle Spectrograph (UVES) instrument at ESO’s Very Large Telescope (VLT). Under the assumption of predominantly zonal flow, this method allows the simultaneous direct measurement of the zonal velocity across a range of latitudes and local times. The technique, based on long slit spectroscopy combined with the high spatial resolution provided by the VLT, has provided the first ground-based characterization of the latitudinal profile of zonal wind in the atmosphere of Saturn and the first zonal wind field map in the visible. It promises to improve the characterization of the equatorial jet and the latitudinal variation of the zonal winds, as well the measurement (and monitorization) of its spatial and temporal variability, achieving a better understanding of the dynamics of Saturn’s zonal winds (which Sánchez-Lavega have found to have changed in recent years). A complete characterization of the dynamical behaviour of Saturn atmosphere is crucial for understanding its driving mechanisms. Finally, the complementarity with Cassini, has provided an independent set of observations to compare with and help validate the method. The zonal wind profile retrieved is consistent with previous spacecraft measurements based on cloud tracking, but with non-negligible variability in local time (longitude) and in latitude.
Figure 2: Geometry of the slit positions at the observation days. Saturn’s diameter is 17.4", and the slit aperture is 0,3”x25” . The aperture offset between consecutive exposures is 1". The sub-terrestrial point is at -26.1ºS.
The UVES/VLT instrument has been used, which simultaneously achieves high spectral resolving power and high spatial resolution. The field has been derotated in order to have the aperture aligned perpendicularly to Saturn’s rotation axis. In this configuration, spatial information in the East-West direction is preserved in a set of spectra in the direction perpendicular to dispersion. Our Doppler velocimetry method is based on the technique of absolute accelerometry (Connes, 1985) which has been applied to the backscattered solar spectrum in order to determine the Doppler shift associated with the zonal circulation. Our measurements have been made in the wavelength range of 480-680 nm. Previously we successfully adapted and fine tuned this Doppler velocimetry technique for measuring winds at Venus cloud tops (Machado et al. 2012, 2014,2017, 2021; Gonçalves et al., 2020). In the present study we will show the adaptation of this method for Saturn’s case. We will use coordinated observations from the Cassini’s Visible and Infrared Mapping Spectrometer (VIMS), in order to compare with the Doppler winds obtained from the UVES/VLT high-resolution spectra.
The observations consisted of 4 blocks of 15 exposures of 90 sec, plus two shorter blocks of 9 exposures, totaling 7.3 hours of telescope time. In order to cover the whole disk the aperture has been offset by 1 arcsec in the North-South direction between consecutive exposures. Most of the northern hemisphere was covered by the rings. Saturn’s diameter was 17.4 arcsec, and the slit aperture was 0.3x25 arcsec. The aperture offset between consecutive exposures was 1 arcsec. Two shorter observations blocks of 9 exposures only covered the central part of the disk, and four others covered the whole disk. The sub-terrestrial point was at -26.1 S. The presence of the rings lead to severe order superposition. The dark region between the rings and the disk may or may not be present, depending on the slit position. On the other hand, defects in the response of the UVES slit in the upper part preclude its use for accurate Doppler measurements such as these. For these reasons only the central part of the aperture has been considered for the measurements.
It can be easily noticed that we were able to reproduce with a significant agreement the amplitudes of the wind velocities previously observed in a vast range of latitudes and that they are highly consistent with the cloud tracking measurements from almost simultaneous Cassini data.
Figure 3: Contour map of Saturn disk for the first night of observations. The wind velocities have units of m/s. Thecolor scale was arbitrary.
References
Connes, P., Absolute Astronomical Accelerometry, Astrophysics and Space Science (ISSN 0004-640X), volume 110, no. 2, p.211-255, 1985.
Goncalves, R., Machado, et al., Icarus, 335, article id. 113418, 2020.
Machado, P., Luz, D.Widemann, T., Lellouch, E.,Witasse, O, , Icarus, Volume 221, p. 248-261, 2012.
Machado, P., Widemann, T., Luz, D., Peralta, J., Icarus, 2014.
Machado, P., Widemann, T., Peralta, J., Gonçalves, R., Donati, J-F., Luz, D., Icarus, 285, 8-26, 2017
Machado, P., et al., Atmosphere, 12, 506, 2021.
Sánchez-Lavega, A., et al., Nature, 423, 623-625, 2003.
Sánchez-Lavega, A., Hueso, R.; Pérez-Hoyos, S., Icarus, 187, 510-519, 2007.
Sánchez-Lavega, A., et al., Nature Communications, 7, id. 13262, 2016.
How to cite: Machado, P., Silva, M., Sánchez-Lavega, A., Silva, J., Espadinha, D., Brasil, F., and Ribeiro, J.: Saturn atmosphere's winds with VLT/UVES Doppler velocimetry, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-354, https://doi.org/10.5194/epsc2022-354, 2022.
Titan’s atmosphere includes many trace hydrocarbon and nitrile species that reach their condensation temperatures in the stratosphere. These, for the most part, will condense out as ices given sufficient condensation nuclei, which are provided by the organic haze particles. Barth (2017) explored the physics behind the size and abundance of pure ice particles that could be present in Titan’s atmosphere and found they would condense out in layers between about 80 and 60 km given thermal conditions at the Huygens landing site (Fig. 1).
We now expand that study to multiple latitudes and include mixtures of trace species in the ice particles. Anderson et al. (2018) have shown that in Titan’s stratosphere, where many of the trace gases are saturated at the same altitude, they are likely co-condensing onto the haze particles. This changes the optical properties of the particles, but microphysically the formation process is similar to modeling the pure ices, as long as the vapor pressures are adjusted for the mixture.
Modeling is done using the Community and Aerosol Radiation Model for Atmospheres (CARMA; Barth 2020). CARMA models the physics of vertical transport and coagulation in a column of atmosphere and the interaction of particles and gases through nucleation, condensation, and evaporation. The growth routines have been modified to include particles composed of multiple volatiles, with each volatile component growing or evaporating in response to the environment (Barth & Toon, 2006). Particles are represented by a number of discrete mass bins, such that the size distribution of ice particles can be explored at all altitudes in the column. The model keeps track of the changes with time of the number of particles (including core mass for clouds) and mass density of volatiles.
This work is supported by NASA CDAP 80NSSC20K0485.
References: Anderson, C. M., R. E. Samuelson and D. Nna-Mvondo 2018. Organic ices in Titan’s stratosphere. Space Sci. Rev. 214, 125; Barth, E.L. 2020. PlanetCARMA: A New Framework for Studying Planetary Atmospheres. Atmosphere, 11(10), 1064; Barth, E. L. 2017. Modeling survey of ices in Titan’s stratosphere. Planet. Space Sci. 137, 20–31; Barth, E. L., and O. B. Toon 2006. Methane, ethane, and mixed clouds in Titan’s atmosphere: Properties derived from microphysical modeling. Icarus 182, 230–250.
How to cite: Barth, E. L.: Microphysical modeling of mixed composition ices in Titan’s stratosphere, Europlanet Science Congress 2022, Granada, Spain, 18–23 Sep 2022, EPSC2022-765, https://doi.org/10.5194/epsc2022-765, 2022.