Scalable E(3) Equivariant Graph Neural Networks for Particle Simulations

Introduction

The final phase of planet formation involves the growth of planetesimals through pairwise collisions of bodies up to the size of planets in protoplanetary discs. Studying this final phase, numerical methods are used to investigate collisions and thus the formation of planets.
N-body simulations can be used to model the dynamical evolution of circumstellar disks, including planet formation [1]. Gravitational N-body models fail as soon as the bodies touch, hence models for treating collisions must be added. A general and flexible approach by Burger et al. [1] resolves collisions by running dedicated Smoothed Particle Hydrodynamics (SPH) simulations for each collision.
Accurate methods, such as SPH, are computationally intensive and time-consuming. To achieve faster, yet accurate results, there are approaches using different machine learning (ML) methods on SPH datasets. Winter et al. [2] use comprehensive SPH datasets including rotating bodies. They utilize ML models (instead of SPH) to predict collision outcomes. 

Independent from planet formation, recently, neural networks have been successfully applied to the approximation of numerical N-body and particle-based fluid dynamics simulations. They utilize graph neural networks (GNN) to handle particle representations, e.g. point clouds like SPH representations. In addition, Martinkus et al. [3] introduce GNNs with a hierarchical architecture to handle large numbers of particles. Current approaches use equivariant neural networks that induce geometric properties. Inductive biases such as E(3)-equivariance might lead to faster training convergence and improved generalization.

Aim of this work

Classical simulation methods for planetary collisions are particle-based. However, previous machine learning approaches for planetary collisions do not use particle-based models and mainly consider macroscopic properties of collisions. Such methods allow physical interpretation only to a certain degree. A more general approach requires modelling small-scale physical interactions as in the particle based classical methods.
Therefore, we develop a model for particle-based simulations that is suitable for complex simulations such as planetary collisions. We propose combining equivariant graph neural networks with a hierarchical tree architecture. This enables learning SPH particle representations directly by processing scalar and vectorial physical quantities in a scalable manner. Since calculating all particle interactions scales quadratically with the number of particles (O(n²)), dense connectivity becomes costly in case of many particles. Therefore, the hierarchical tree architecture is used similar to classical numerical particle simulation techniques to approximate the interactions of long-range forces. The utilized hierarchical tree reduces the computational complexity to O(n) in the tree and O(n log(n)) for building the tree while retaining long-range interactions like gravity.
So, our ML model replaces SPH simulations for planetary collisions within classical N-body frameworks. 

Methods

Dataset:
We use a small SPH dataset derived from the dataset by Winter et al. [2] which is based on statistics derived from Burger et al. [1]. The dataset includes pure hydrodynamic SPH simulations with self-gravity of pairwise planetary collisions with varying collision angles and velocities. Bodies consist of iron cores and basalt mantles of different sizes.

Model:
We take SPH representations as a point cloud and build a graph by representing the interactions with the neighbour particles for every particle by edges. Our model is based on a scalable E(3)-equivariant GNN (SEGNN) [4]. To create a model that is scalable to high numbers of particles, we add a hierarchical graph architecture inspired by the fast multipole method [3] and call it hierarchical SEGNN (HSEGNN).
SEGNN takes graphs with fixed numbers of neighbours using a KNN algorithm to find the connected neighbours and applies equivariant convolutions on that graph. The connections in the hierarchical graph are derived by the tree algorithm.

We use an autoregressive model which iteratively predicts the state after a fixed time step from an initial state. These ML time steps can be much larger than the classical simulation time steps. Our models are trained with common, gradient-based optimization methods.

Results

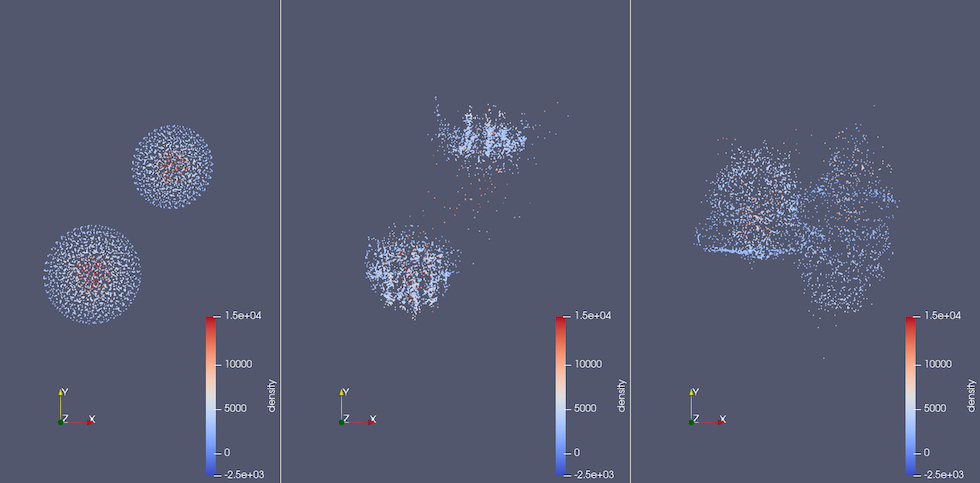
a) Time step 3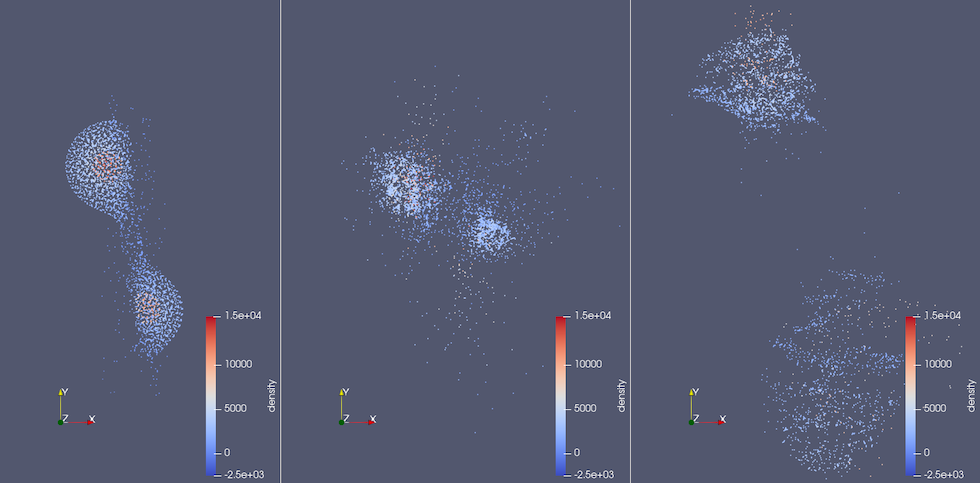

b) Time step 6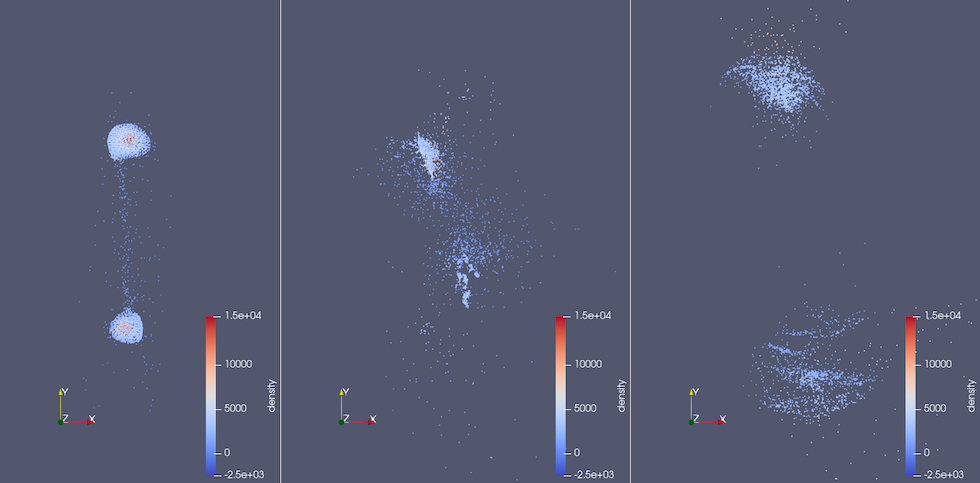

c) Time step 10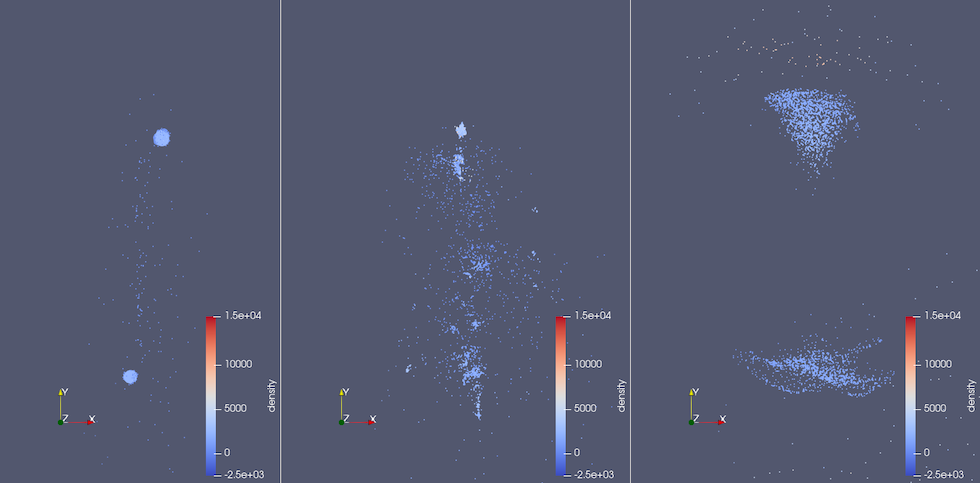

d) Time step 25

Figure 1.: Collision time steps' ground truth (left), prediction of the HSEGNN (middle) and prediction of the SEGNN (right) before and during collision. Each SPH particle is represented as a point. The ML time steps 3,6,10 and 25 are shown from top to bottom. One ML time step corresponds to 10 minutes in simulation time. The density is color-coded.

Figure 1 shows snapshots of one of our test simulations. Colour scales indicate rough boundaries between iron cores and basalt mantles. Both HSEGNN and SEGNN capture the overall evolution of large fragments to a certain extent while suffering from unrealistic predictions on smaller scales. However, HSEGNN retains individual fragments better than SEGNN which suffers from unrealistic diffusion artefacts.
We conclude that although both methods require improvements to produce physically plausible results, HSEGNN shows improved capabilities for mapping material forces within fragments.

Runtime:
The ML models achieve speed advantages by a factor of 100 compared to the SPH simulations. However, the duration to build the hierarchical graph is within the runtime range of the SPH simulations. The implementation of our tree algorithm has capabilities for speed improvements to make the overall model faster than the SPH simulations. Shorter runtimes are the main advantage of ML methods over classic simulation methods in this application.

Acknowledgements

The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 37/935-1 FUGG.

References

[1] Burger, C., Á.  Bazsó, and C. M. Schäfer (2020). “Realistic collisional water transport during terrestrial planet formation”. In: Astronomy & Astrophysics 634, A76.

[2] Winter, Philip M. et al. (2023). “Residual neural networks for the prediction of planetary collision outcomes”. In: Monthly Notices of the Royal Astronomical Society 520.1, pp. 1224–1242.

[3] Martinkus, Karolis, Aurelien Lucchi, and Nathanaël Perraudin (2021). “Scalable Graph Networks for Particle Simulations”. In: Proceedings of the AAAI Conference on Artificial Intelligence 35.10, pp. 8912–8920.

[4] Brandstetter, Johannes et al. (2022). “Geometric and Physical Quantities improve E(3) Equivariant Message Passing”. In: International Conference on Learning Representations.