A New Model of the Litospheric Magnetic Field of Mars using a Physic-Informed Neural Network

Introduction:  Mars possesses a strong remanent crustal field, indicative of an ancient magnetic dynamo which is now inactive [1]. Such a dynamo is associated with the internal composition and thermal evolution of early Mars. Thus, crustal magnetic fields record invaluable insights into the early stages of this planet, and our objective is to map out their distribution. We address the problem of modelling the crustal magnetic field using magnetometer measurements from two orbiters, MGS and MAVEN. A substantial amount of additional low-altitude data has been collected by MAVEN since the most recent and highest resolution global model was published ([3], referred to as L19 in the following), thereby necessitating a new model to be computed. Two approaches were formally used for this: Spherical Harmonics (SH, e.g., [2]) and Equivalent Source Dipoles (ESD, e.g., [3]). We propose to solve this regression problem with Physics-Informed Neural Networks (PINN). Intuitively, this method is comparable to that of a Spherical Harmonic model, with basis functions that are not a priori defined but uniquely suited to the regression task at hand. We show that this alternative has multiple advantages such as computational efficiency and robustness to sparse distributions.

Data:  MGS (1997 – 2006) and MAVEN (since 2014) provided time series of the magnetic field measured at orbital altitude. While MGS was in a nearly constant altitude orbit most of the time, MAVEN has a much more eccentric orbit. This offers the advantage of probing the entire magnetic field environment but also lacks repeated orbits. Because low altitude data contains small-wavelength information, a model including the latest lower-altitude data from MAVEN should theoretically enhance the resolution of small-scale features.

Modelling: Physics-informed neural networks (PINN) embed the knowledge of any physical laws that govern a given dataset in the learning process of a neural network. For our crustal field model, the network takes three parameters as input, point coordinates, and outputs a scalar potential. The free parameters, analogous to dipole components for the ESD approach, or to Gauss coefficients for SH, are the weights and biases of each neuron in the network that connect inputs and outputs through an array of interconnected layers. The predicted B-field is computed from this scalar potential with automatic differentiation before updating the free parameters with back-propagation.

The datasets from MGS and MAVEN orbiters differ too greatly to be treated equivalently. The former represents densely collected data at nearly constant altitude, whereas the latter is sparse, but distributed across a larger altitude range including lower altitudes. We therefore adapt our modelling strategy to these characteristics. A network is trained for each altitude band independently and the resulting preliminary models are used to remove outliers from the data.

A problem with inputs in spherical coordinates is that of model continuity at poles and along the longitude boundary. The model does not inherently know that longitude 180° is equal to longitude -180°. To overcome this issue without loss of accuracy, one could either reparametrize the data into cartesian coordinates or decompose the periodic component into a weighted summation of the basis functions of Fourier series. Given that neural networks are approximators of nonlinear continuous functions, the sole first two basis functions suffice [4].

Discussion:  There are four main reasons why we believe that PINN can perform better in achieving this regression. First of all, for a given regression task, neural networks are more memory-efficient than traditional least-squares methods like SH or ESD which require inverting large matrices. This circumvents the former necessity of down sampling the extensive datasets, thereby losing information. Second, modern neural network algorithms come with an arsenal of tools enabling to find the optimum between under and over-fitting of the data, such as validation and early stopping, without explicit regularizations. Thirdly, PINN is a very powerful method to discriminate the data according to any physical assumptions we may have. For instance, imposing ∇×B = 0 as a soft constraint will reward field data originating from the crust that is conservative and punish field data that results from induced currents in the ionosphere. Lastly, this method combines the benefits of both SH and ESD. The ESD method was proposed as an alternative to SH for its robustness to data sparsity [5]. However, ESD has the disadvantage of being inherently ill-conditioned – the Gram matrix becomes less invertible as spatial resolution improves [6]. PINN is impacted by neither of these issues.

First Results and Outlook:  The first results from this novel approach are promising. Fig. 2 shows the observed magnetic field components along a quiet orbit of MAVEN compared with predictions by the L19 model [3], and by our early model (outliers not yet filtered). We can observe that it is locally outperforming L19. Moreover, a 200km map of the predicted scalar field using our PINN model and the unfiltered MAVEN data shows an unprecedented resolution (Fig. 3). Even though we did not use any regularization, nor down sampled the data, we do not observe linear features following individuals tracks, a typical feature for unregularized models. This observed smoothness indicates that the data is not overfitted.

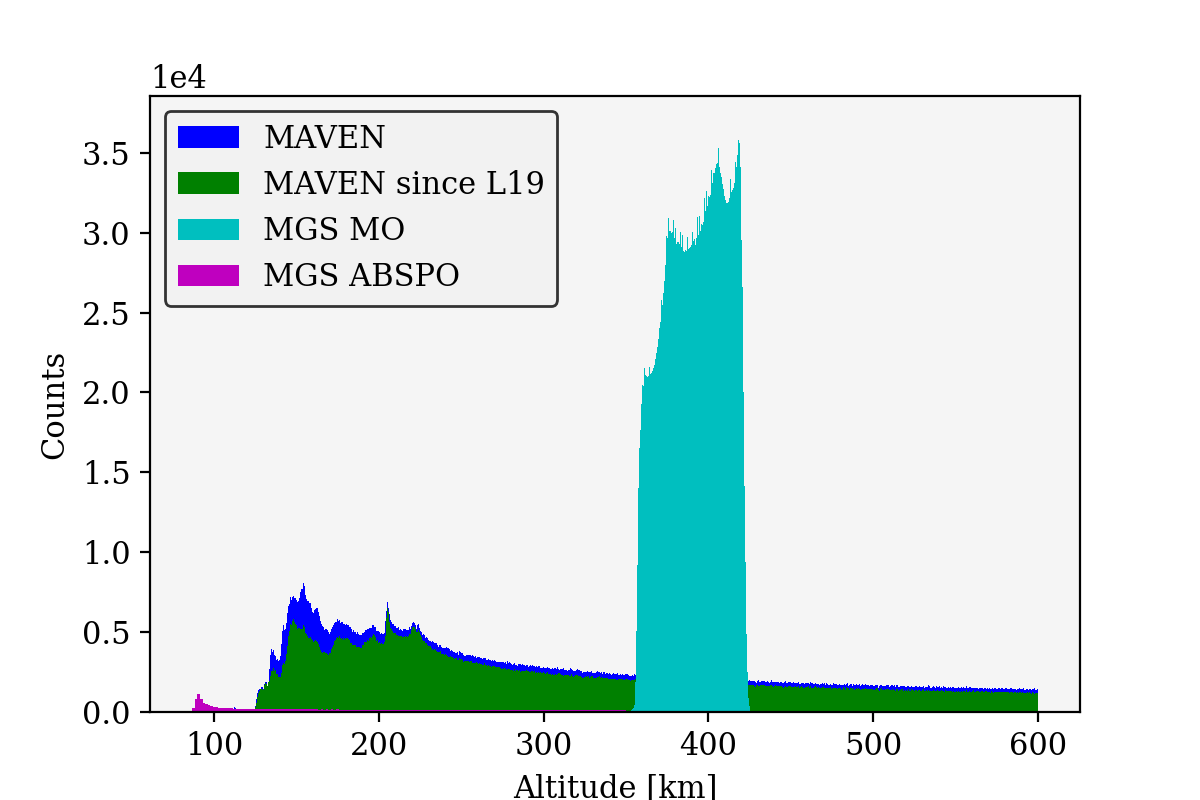
Fig.1: Histogram of the altitude distribution of the nighttime data from MGS and MAVEN orbiters. An important part of the low-altitude data has been produced after the last global model L19 [3].

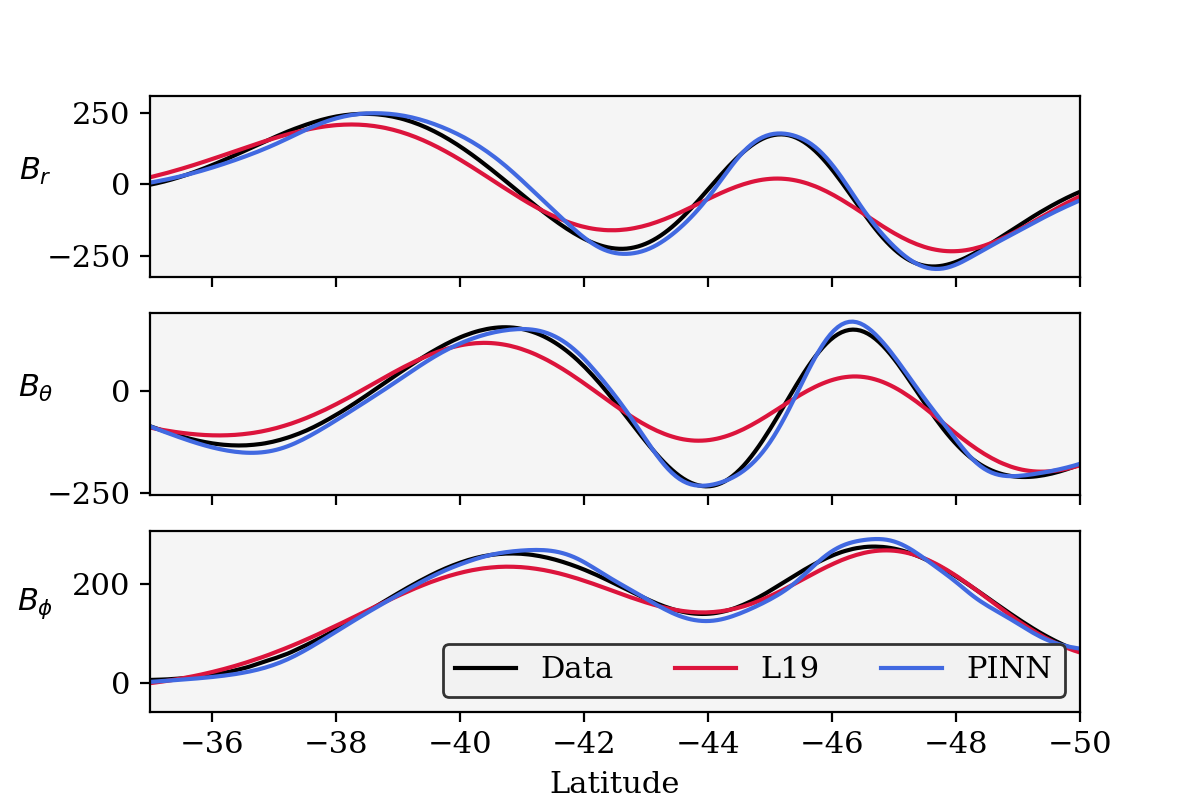
Fig.2: Observed and predicted magnetic field along an orbit of MAVEN (23-04-2023). PINN has more predictive value than L19 [3] for quiet orbits.

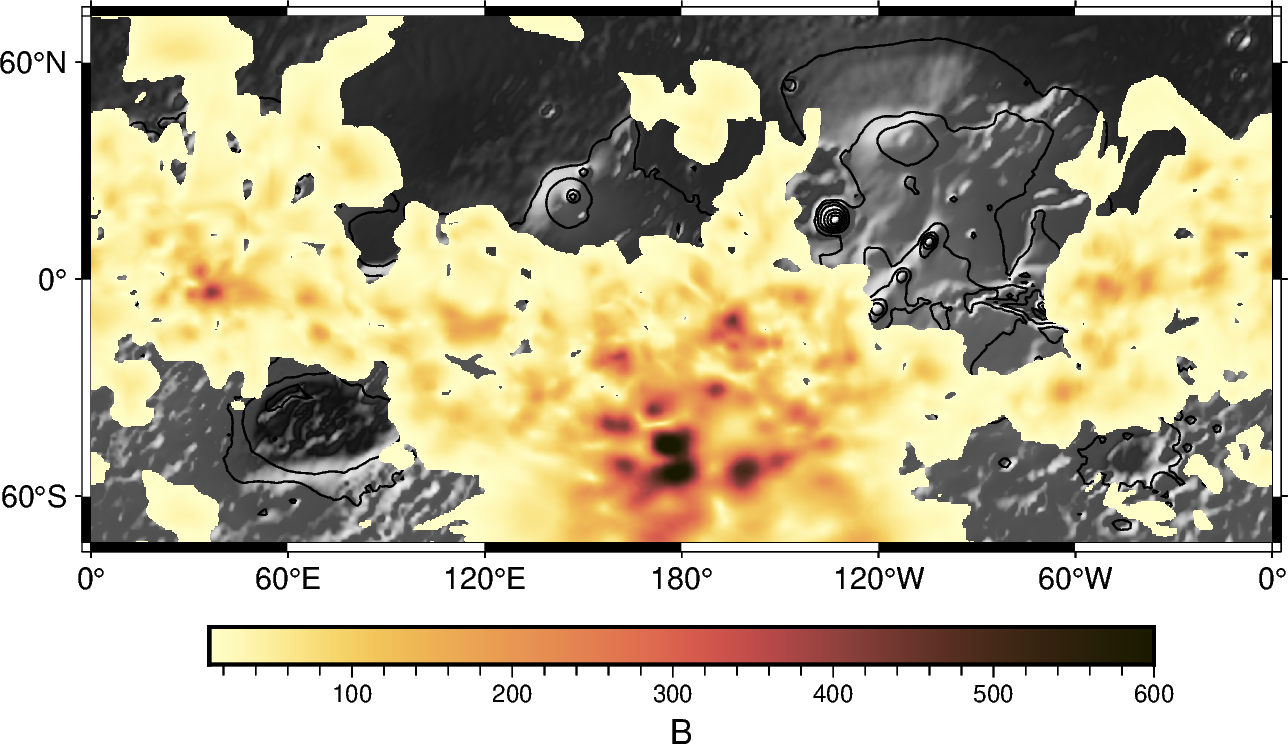
Fig.3: Map of the predicted scalar field at 200km using our PINN model and the unfiltered MAVEN data only.

Acknowledgments: This work is supported by SNF Ambizione (PZ00P2_209123).

References: [1] Acuna et al. (1999) Science, xx.  [2] Morschhauser, A., et al. (2014) Journal of Geophysical Research: Planets 119.6, 1162-1188. [3] Langlais, B., et al. (2019) Journal of Geophysical Research: Planets 124.6, 1542-1569. [4] Lu, L., et al. (2021) SIAM Journal on Scientific Computing, 43(6), B1105-B1132. [5] Mayhew, M. A., and Estes, R. H. (1982) NAS 1.26: 169604. [6] Blakely, R. J. (1996) Cambridge University Press.