The dense resonance meshes around the ringed Chariklo, Haumea and Quaoar

We consider the effect of Spin-Orbit Resonances (SORs) excited on ring particles by bodies with non-axisymmetric gravitational fields. SORs happen for n/Ω ~ m/(m-j) , where n is the mean motion of the ring particles, Ω is the spin rate of the body, m is an integer (positive or negative) and j>0 is the order of the SOR. Due to the structure of their phase portraits, only first- and second-order SORs are expected to significantly excite eccentricities on dense collisional rings.

We calculate more specifically the eccentricities excited at SORs around Chariklo, Haumea and Quaoar, considering in turn the effects of their triaxiality and the effects of a mass anomaly μ=10^-3  relative to the mass of the central body. The triaxiality is obtained from stellar occultation results, while μ=10^-3 is a typical estimated value corresponding to topographic features (mountains, depressions,...) of several kilometers in height or depth. The results are displayed in Figs. 1, 2 and 3, corresponding respectiveley to Chariklo, Haumea and Quaoar. We find that the triaxialities of all three bodies excite large eccentricities (e>0.1) on the ring particles, resulting in unstable orbits that suffer strong torques from the SORs, chaoticity due to the superimposition of SORs, or even short-term physical collisions with the body.

As a consequence, all the region inside the 1/2 (or 2/4) SOR is not prone to host stable rings around Chariklo and Haumea. Moving outward, the 1/3 SOR excites moderate eccentrities of the order of e=0 01 on the particles of Chariklo's and Haumea's rings, thus avoiding a rapid destruction of these rings. In the case of Quaoar, the 1/3  and 5/7 SORs excite eccentricities of a few 10^-3 only, preventing again a rapid ring destruction.

A companion paper by Salo and Sicardy presents N-body simulations showing that the 1/3 second-order SOR can indeed cause a single-sided confinement, thus explaining the current location of the main rings of Chariklo, Haumea and Quaoar. More simulations are required to explore the stability of the second ring of Quaoar (Q2R) that orbits near the 5/7 second-order SOR. This resonance is surrounded by strong first-order SORs (Fig. 3) that may destabilize Q2R. A better assessment of Quaoar's triaxial shape and mass anomaly μ must be now undertaken for discussing further the stability of this ring.

Acknowledgments. BS thanks the French ANR “ROCHE" for support.

 

Fig. 1 - Eccentricities forced on a particle with an initially circular orbit around Chariklo. Left: first-order SORs, red: resonances forced by the triaxial shape of Chariklo, black: resonances forced by a mass anomaly of μ=10^-3. Right: second-order resonances, blue: effect of the triaxial shape of Chariklo, black: effect of a mass anomaly μ=10^-3.

Fig. 2 - The same as Fig. 1 for Haumea.

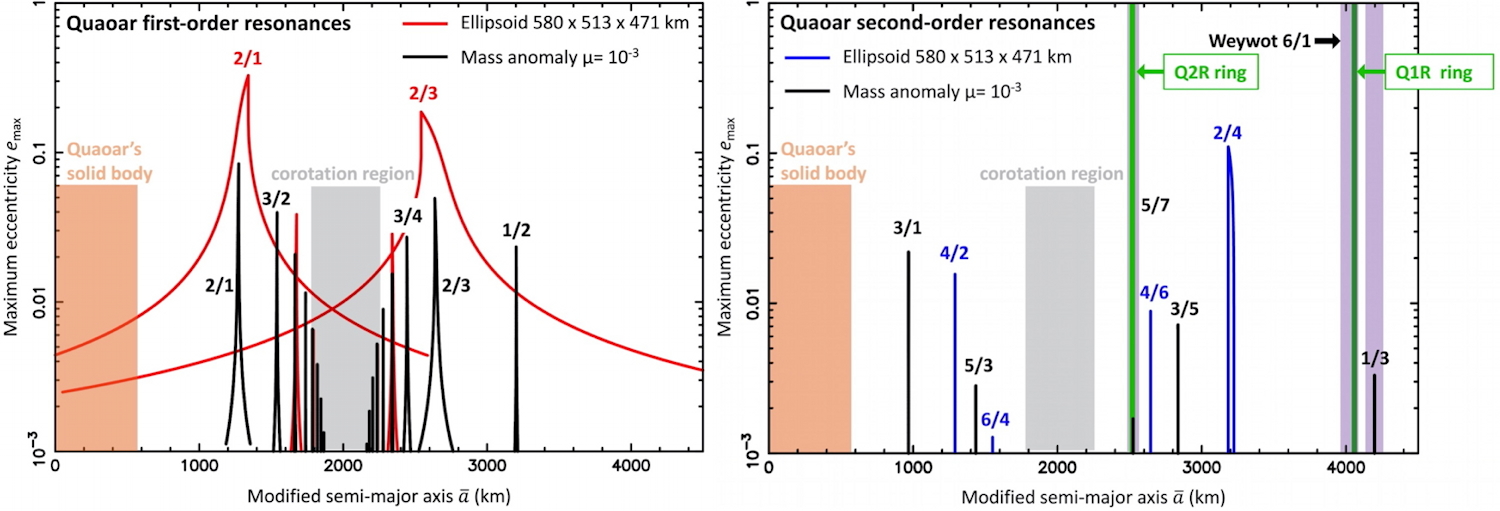
Fig. 3 - The same as Fig. 1 for Quaoar.