A Reverse Monte Carlo Method to Investigate the Topography Interaction with the Lunar Exosphere

Introduction

Many Monte Carlo-based models of exospheres of our solar system have been developed in the past, for example, by Hodges et al. (1973), Crider et al. (2002), Grava et al. (2014), Hurley et al. (2017), Killen et al. (2019), Kegerreis (2020), Schörghofer et al. (2021), and Smolka et al. (2023). Their main setup includes tracking individual particles from a defined source of the exosphere to the eventual loss of the particles in a forward manner. Due to the size of the particle trajectories through the exosphere, which can span over more than half the Moon’s circumference, the simulations must geometrically include the entire Moon. While this is an excellent tool for investigating global effects and overarching exospheric dynamics, its accuracy on a significantly smaller scale is lower. The smaller the region of interest and, thus, the relevant domain, the less likely it is for any particles of the global simulation to travel through this volume, which negatively impacts the resolution of the output.

 

There are several such scenarios where a traditional Monte Carlo simulation of an exosphere is not ideally suited for the problem, including investigating local and regional topography and its influence on the exosphere. To tackle this problem, we are implementing a reverse Monte Carlo (RMC) method into existing exosphere simulation frameworks, where, instead of tracking a particle from its source to its loss, the simulation starts the particle inside the relevant domain and evaluates the likelihood of this assumption by backtracking its trajectory. This ensures that every simulated particle contributes to the investigation of the region of interest, which greatly reduces the computational effort and increases the resolution of the output. While this method is already used in other applications like the radiative transfer in exospheres (Gratiy et al., 2010), it has not yet been applied to particle tracking in exosphere models. The following section describes the numerical model and its internal mathematical structure.

 

Numerical Model

The main problem of reverse tracking particle trajectories in exosphere models is the unknown kinetic energy of the particle. A backwards trajectory leads from the known landing position, x₁, to the unknown starting position, x₀. Generally, the shape of the trajectory, including the angular and speed distribution of the launch velocity, is based on the processes that lead to the release of the particle at x₀. Since this information is inaccessible a priori, the reverse model must include a probabilistic approach to the particle’s kinetic energy with a weighing factor that is calculated posteriorly.

 

Mathematically speaking, let the particle start its reverse journey at x₁, where it draws a landing velocity vector v₁ based on a velocity distribution V₁ with probability density p₁. The reverse trajectory uses the vector −v₁ as its starting velocity and backtracks the particle to its actual launch position x₀, where it lands with a velocity of −v₀. Based on the conditions and processes occurring at x₀, the probability density p₀ for drawing v₀ from V₀ can be calculated.

 

Using Bayes’ theorem with the events A that the particle launched at x₀ and B that the trajectory in question occurred, p(B) = p₁ is the evidence of the trajectory and p(BA) = p₀ is the conditional probability of the trajectory given that a particle was launched at x₀, leaving only the prior probability p(A) of a particle being launched at x₀ to be determined. Together, one can evaluate the weight w of the reverse trajectory as

If multiple hops of a particle are tracked using the RMC method, each i-th trajectory gets assigned its respective weight w_i, where the prior probability of launch p(A)_i is equal to the weight of the next reverse trajectory, w_i+1. Thus, the i-th weight can be recursively calculated as

with a total of N trajectories and an initial launching probability of p(A)_N.

 

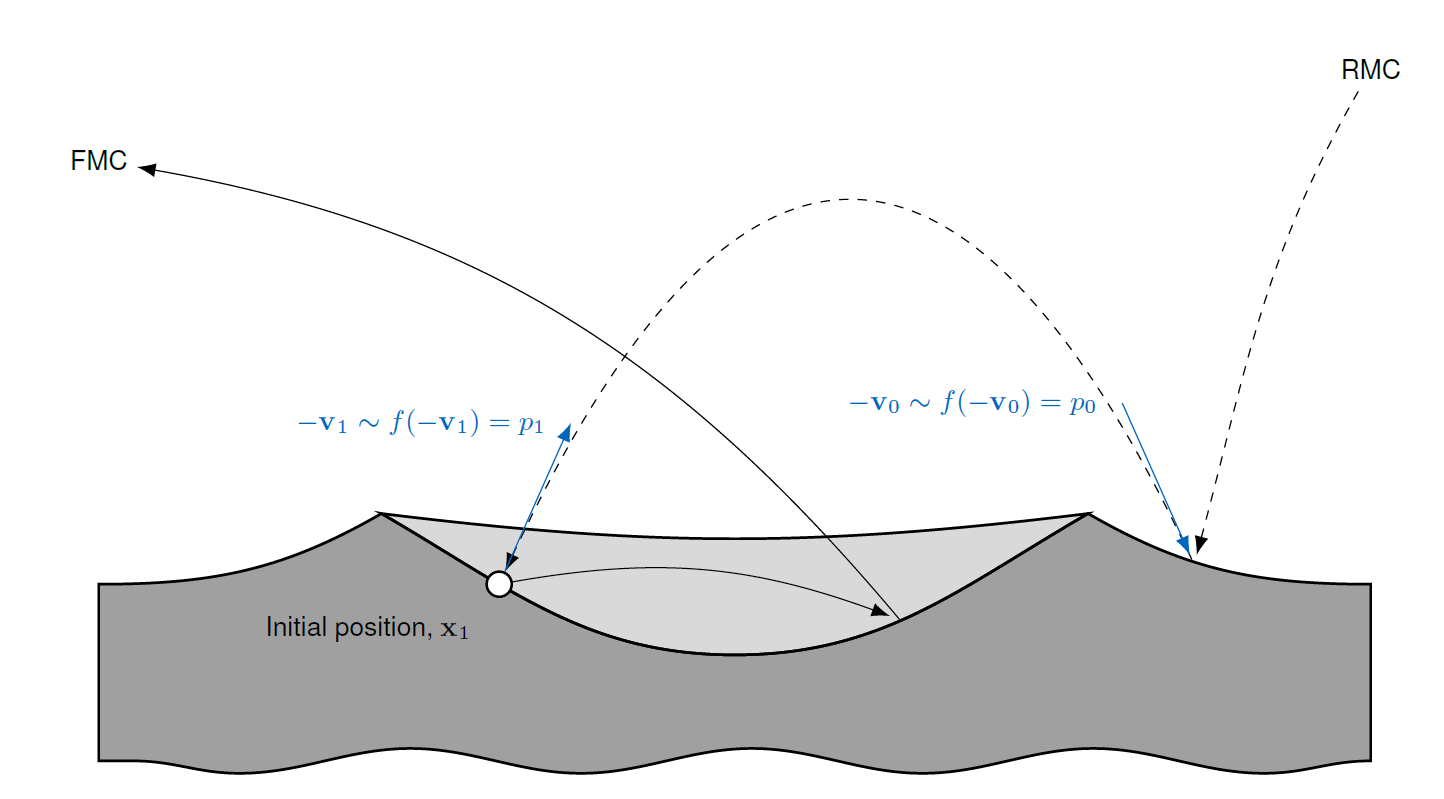
The principle is shown in Fig. 1, where from an initial position x₁, a particle is tracked backwards using the RMC method. The drawn velocities and probabilities are shown in blue. This process can be repeated for multiple hops of the particle until it leaves the computational domain or has come from a known source with a known probability distribution. While p₀ and p₁ can be directly calculated based on the underlying process, for example, using Maxwellian velocity distributions for thermally desorbed exospheric particles, the prior probability p(A)_N has to be estimated either based the conditions at the first x₀ outside of the computational domain. A first-order approximation would assume that p(A)_N is linearly dependent on the particle number density at x₀.

 

Model Scenarios

The main scenario investigated is the interaction of the lunar exosphere with local topography. First, to validate the numerical method, the model is tested with a perfectly flat surface, and the results are compared with the global results of an exosphere simulation. We use Helium particles to further reduce the complexity of the entire model and compare the results with our global model (Smolka et al., 2023). The next step will include a simplified crater geometry where, based on the crater sizes (depth and diameter), we will investigate the exosphere dynamics above and landing probabilities inside the crater. The latter will shed light on whether particles have a preferred landing position inside the crater, which could be used for further studies of permanently shadowed regions and, in extension, the accumulation of volatile species within.

 

Additionally, the method will be used to study the interaction of instruments like mass spectrometers with the lunar exosphere. Particles can be launched from the instrument and tracked backwards to evaluate the likelihood of reaching the instrument. This can be used to optimize the instrument’s position and orientation and estimate the expected particle flux and the required measurement time.

 

Bibliography

• Crider et al. (2002). Advances in Space Research
• Gratiy et al. (2010). Icarus
• Grava et al. (2014). Icarus
• Hodges et al. (1973). Fourth Lunar Science Conference
• Hurley et al. (2017). Icarus
• Kegerreis (2020). Springer Theses Ser.
• Killen et al. (2019). Icarus
• Schörghofer et al. (2021). Space Science Reviews
• Smolka et al. (2023). Icarus