Image Classification of Retrograde Resonance in the Planar Circular Restricted Three-Body Problem

1. Introduction

The advancement of computational techniques and methods such as artificial intelligence applied to celestial mechanics, including image classification. These techniques have been applied in the identification of mean motion resonances for asteroids (Smirnov and Markov, 2017; Carruba et al., 2021) and secular resonances for asteroids Carruba et al. (2022). The rapid growth of machine learning methods applications enables us to leverage these tools for the investigation of dynamical systems such as asteroid and planetary dynamics.

In the restricted three-body problem (R3BP), prograde orbits are those with an inclination less than 90 degrees with respect to the orbital plane of the perturber. Retrograde orbits are defined is this case with an inclination higher than 90 degrees (Morais and Namouni, 2017). These retrograde orbits can occur due to a range of astronomical events, such as collisions, close encounters and dissipation. This study aims to present a machine learning image classification method in order to search for periodic and quasi-periodic orbits, for example, retrograde orbits in the R3BP.

2. Resonances, resonant argument and perturbations

We establish the empirical case by defining μ ≤ 0.01, where μ is the mass ratio between the primaries. This threshold is determined after performing several tests involving different resonances. For values of 0.01 < μ < 0.3, there are only a few instances where the resonant argument can be reliably for identification. This observation could change based on the nature of the orbit. The chosen resonances for investigation are 1/-2, 2/-1, and 1/-1 (Morais and Namouni, 2013). The resonant argument (ϕ) in the Circular R3BP (CR3BP) is defined by ϕ = −pλp − qλ + (p + q)ϖ, where λ and λp are the respective longitudes of the massless and the secondary bodies, and ϖ represents the longitude of the pericenter of the massless body Morais and Namouni (2013). As an example we show the 2/-1 resonance presented in Figure 1, for μ = 0.02, we can still use the resonant argument as a way to identify this resonance, but we cannot determine only by the resonant argument whether it is the center of the resonant due to the amplitude. For μ = 0.1, the resonant argument cannot be analyzed for resonance identification.

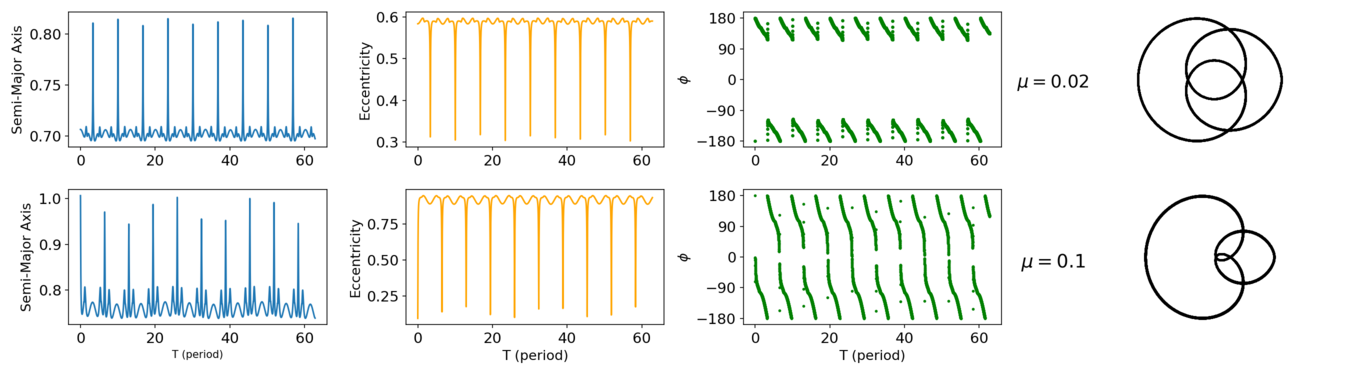
Figure (1): Examples of the osculating orbital elements and resonant argument for the resonance 2/-1.

In fact, when investigating families of periodic/quasi-periodic orbits using classical approaches, we could rely on the amplitude of the resonant argument and the libration mode for identification Caritá et al. (2022). For high mass ratio cases, this analysis could lead to partial results and misinterpretation.

3. Convolution Neural Network Model

A Convolutional Neural Network is a type of artificial neural network commonly used for image recognition and classification, emulating human abilities. The core concept involves building convolutional layers that apply filters, followed by a non-linear function to recognize image data patterns. In this study, we aim to identify resonant families by classifying mean motion resonances using their orbits (x, y) as an image parameter.

For the empirical problem of the planar CR3BP (PCR3BP) we considered the classes of the retrograde mean motion categorized as 1-1Phi0, 1-1Phi180, 1-2Phi0, 1-2Phi180, 2-1Phi0, 2-1Phi180, circular orbits and undefined. These classes represent resonances with libration at 0 or 180, and circular orbits. Figure 2 illustrates examples. Further details on the model parameters can be found in Caritá et al. (2024). As a validation benchmark, we obtained the 1/-2, 1/-1 and 2/-1 from Morais et al. (2021), Morais and Namouni (2019), and Kotoulas and Voyatzis (2020). The Figure 3 illustrates the output of the CNN prediction model successfully identifying circular, 1/-1, 1/-2, and 2/-1 resonant families.

Figure (2):  Sample of the data used in the training.

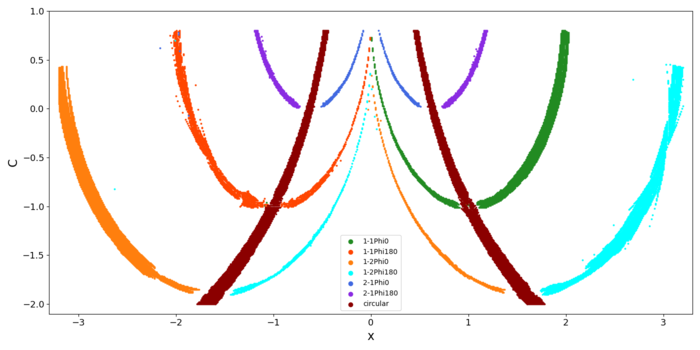
Figure (3):  Classification of the resonances on the right panel.

4. Image resonance classification for high mass ratios in PCR3BP

As the mass of the binary body increases beyond the range of the empirical case, identifying resonances using Keplerian orbital elements becomes challenging due to the two-body problem approximations. However, resonances still exist in the phase space of the dynamical system, and they exhibit a behavior similar to that of empirical orbits in a rotating frame as seen in (Caritá et al., 2023). In Figure 4, the left panel presents the results obtained for a grid with μ = 0.5. The right panel shows the chaotic indicator (MEGNO). We observed a few gaps between some families. The orbits are different for high mass ratios. This could imply in difficulties identifying resonant families as μ increases.

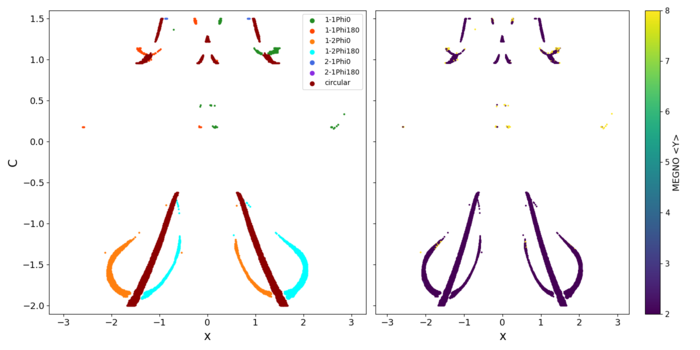
Figure (4): Classification of the resonances for the binary mass ratio of μ = 0.5.

5. Conclusions

The results obtained from the validation of our classification model demonstrate its effectiveness in accurately capturing the distinct patterns and characteristics of retrograde resonances. The model successfully identified retrograde resonances with high accuracy. The versatility of our classification model can extend beyond the constraints of the R3BP, making it adaptable to more intricate celestial environments. The model’s automated approach and efficiency offer researchers a potent tool for exploring a wide parameter space, quantifying stability, characterizing resonant behavior.

References

Smirnov, E.A., Markov, A.B.: MNRAS 469(2),2024-2031 (2017)

Carruba, V. et al, MNRAS, 504(1), 692–700 (2021)

Carruba , V. et al, MNRAS,514(4), 4803–4815 (2022)

Morais, M., Namouni, F., Nature 543(7647),635–636 (2017)

Morais, M., Namouni, F., CMDA, 117(4), 405–421 (2013)

Caritá, G.A et al MNRAS 515(2), 2280–2292 (2022)

Caritá, G.A et al CMDA 136(2), 1–24 (2024)

Morais, M., Namouni, F., CMDA, 133(5), 1-14 (2021)

Morais, M., Namouni, F., CMDA, 490(3), 3799-3805 (2019)

Kotoulas, T., Voyatzis, G., PSS, 182, 104846 (2020)

Caritá, G.A et al NODY 111(18), 17021-17035 (2023)