Efficacy of classical and spectroscopic techniques for strain quantification in weakly shocked rocks: Results from experimentally impacted Taunus quartzite

Traditional strain estimation techniques, such as the Fry and the Rf/Phi method, have been extensively used in tectonically deformed rocks [1]. However, their applicability in impact rocks has not been explored yet. An essential difference between tectonic and impact cratering-led deformation is that the former causes strain rates in the order of 10^-15-10^-6 s^-1 [2], while the latter leads to a much higher strain rate, ~10^-2-10⁶ s^-1 [3]. Furthermore, peak pressures in tectonic deformation are in the order of hundreds of megapascals [4], whereas, in the case of naturally shocked rocks, the shock pressures are in the range of gigapascals [5].

To address this, an impact cratering experiment was carried out on a quartzite block to investigate the efficacy of these traditional and spectroscopic tools in determining strain in weakly shocked rocks (Fig. 1). A basalt projectile of diameter 6.18mm was accelerated to a velocity of ~5km/s and impacted a quartzite block, Taunus quartzite from Germany.

The block was sawed through the crater centre. Twelve cores were recovered from the target surface and the sawed (sub-) surface each. Each cylinder was bisected in half to produce 24 specimens, each from the target and subsurface. Specimens 5.1 to 5.24 were from the target surface, whereas the subsurface specimens were labelled 6.1 to 6.24. Specimens 5.1 to 5.12 and 6.1 to 6.12 were from the top half of the cylindrical core obtained from the target surface and subsurface, respectively. Similarly, 5.13 to 5.24 and 6.13 to 6.24 were from the lower half of the cylindrical core obtained from the target surface and the subsurface, respectively.

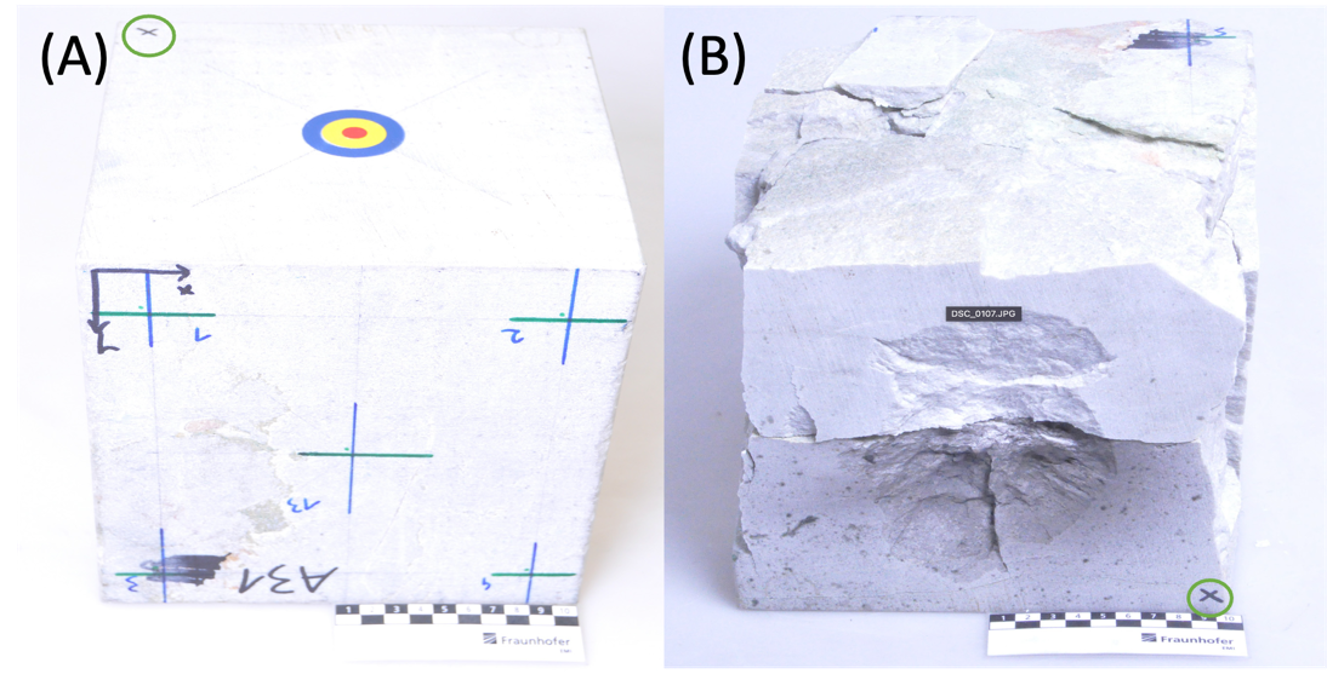
Figure 1: Photographs of the Taunus quartzite block (edge length 20 cm) (A) before and (B) after the impact experiment. The block was split into several pieces after the experiment. The top/target surface is marked with “Top” and “X” inside a green circle. Note the different orientations of the block in the two images.

Strain analysis was carried out using three methods: (1) Fry, (2) Rf/Phi, and (3) X-ray Diffractometry (XRD) in the impacted Taunus quartzite. These results were then compared to simulated strains in the transient stage from hydrocode modelling (Fig. 2). Radial fractures were observed on the target surface but not in the subsurface in the thin section images (Fig. 3). Results demonstrably suggest that the strain measured using the three methods is similar to the results from the hydrocode simulations. Furthermore, these techniques are sensitive enough to capture strain imparted at shock pressures as low as 0.23 GPa (obtained from hydrocode modelling) at the transient crater stage (at 25 µs post impact).

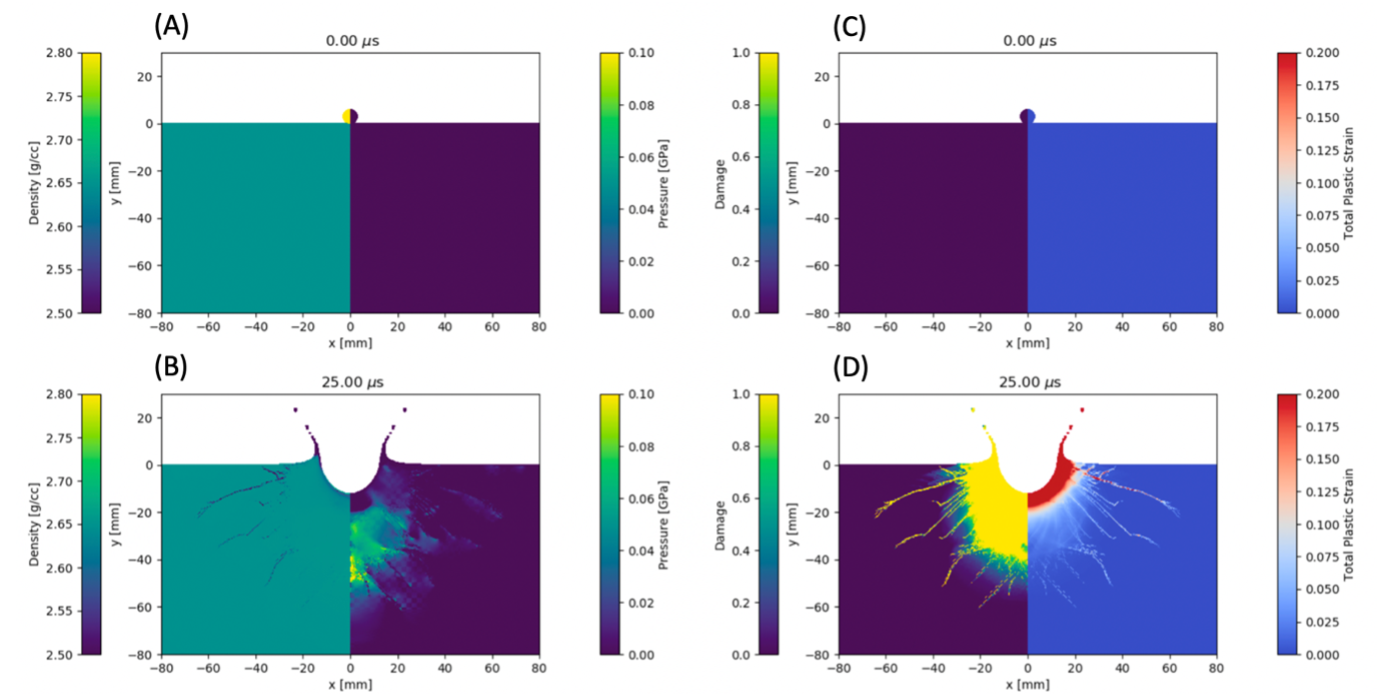
Figure 2: Results from hydrocode simulation. (A-B) show pressure and density distribution, and (C-D) show damage and total plastic strain at 0 ms and 25 ms. Simulation is run till the end of the transient cratering stage and before the arrival of the reflected wave from the free surface.

Figure 3: Thin section images from the experiment. The arrows indicate the direction of the point of impact. (A) Sample T01 is on the target surface and closest to the point of impact, (B) sample S01 is on the subsurface and just below the point of impact, whereas (C) sample S24 is the point farthest away from the point of impact. Note the radial tensile fractures in the target surface in (A) (parallel to the arrow indicating the direction of the impact point) and their absence in the subsurface (B and C).

However, caution is advised while using Fry and Rf/Phi methods, as grain fracturing and pulverisation may affect the grain centre distribution and grain shape, thus leading to anomalous results. The use of the lattice technique, XRD, can be investigated further to understand the accuracy and efficacy in low-strain conditions. 

Acknowledgements:

We thank the Dept. of Earth Sciences at the Indian Institute of Technology-Kanpur for microscopy and XRD facilities. The authors are also grateful to Dr. Auriol Rae for his input and help on the hydrocode simulation. We are also thankful to Dr. Gaurav Joshi for his suggestions. Yashwant Singh helped in the Fry analysis.

References:

[1] Joshi, G., et al. (2017). Microstructures and strain variation: Evidence of multiple splays in the North Almora Thrust Zone, Kumaun Lesser Himalaya, Uttarakhand, India. Tectonophysics 694, 239–248.

[2] Pfiffner, O. A., et al. (1982). Constraints on geological strain rates: Arguments from finite strain states of naturally deformed rocks, J. Geophys. Res., 87(B1), 311–321.

[3] Ramesh, K. T. (2008). High Rates and Impact Experiments. In: Sharpe, W. (eds) Springer Handbook of Experimental Solid Mechanics. Springer Handbooks. Springer, Boston, MA.

[4] Vaughan-Hammon, J. D., et al. (2021). Alpine peak pressure and tectono-metamorphic history of the Monte Rosa nappe: evidence from the cirque du Véraz, upper Ayas valley, Italy. Swiss J Geosci 114, 20.

[5] Engelhardt, W. V., et al. (1969). Shock induced planar deformation structures in quartz from the Ries crater, Germany. Contr. Mineral. and Petrol. 20, 203–234 (1969).