Collisional confinement of 1:3 resonance ringlets around non-spherical bodies

Rings around outer Solar system small bodies are not rare, as exemplified by the rings discovered around Chariklo, Haumea, and Quaoar. The triaxial shapes and smaller topographic features (“mass-anomalies”) of such bodies imply markedly non-axisymmetric gravitational field. This leads to strong excitation of eccentricities at spin-orbit (SOR) resonances, where the particle mean motion n and the spin rate Ω of the central body satisfy n/Ω=m/(m-j), with m either a positive (inside co-rotation) or negative (outside) integer and j>0  is the order of the resonance. As demonstrated in the companion paper by Sicardy&Salo, the region near 1/3 SOR provides the innermost relatively peaceful environment around the central body.

Figure 1 displays simulations of a azimuthally complete 3D ring placed at 1/3 SOR with a mass-anomaly μ=0.1. Non-colliding test particles (upper frame) develop large eccentricities near resonance, which appears as a gap in the distribution of particles. Inclusion of collisions leads to viscous spreading when μ=0 (middle) but when both collisions and resonance perturbations are included, to a formation of a confined ringlet (lower frame). The ringlet formation is preceded by a phase where particles gradually collect to the resonance, their orbits being synchronized by mutual impacts. Such confinement is not specific to 1/3 resonance, but takes place when the ring is sufficiently perturbed with strong width variations. In this case the angular momentum flux reversal takes place and  collisions lead to confinement rather than dispersal.

The accumulation and subsequent confinement represent a competition between viscous diffusion and resonant excitation of eccentricities. Based on timescales of these processes, a simple condition  τ R² < k μ²  can be written for the parameter regime where particle accumulation to the 1/3 resonance is expected. Here k  is a constant, τ denotes dynamical optical depth and R  the particle radius. Fig. 2 (left) displays simulations conducted with τ=0.015,  with different μ and R, confirming the above scaling of the boundary between accumulation and dispersal.  Extrapolating to realistic values of expected μ ≈10^-3 (corresponds to km-sized topographic features, mountains or depressions), implies that resonance accumulation should take place for meter-sized particles, even when for τ ≈1 (see the red line).

During the accumulation of the ringlet,  the ringlet angular momentum L_z   jumps due to torque exerted by the perturbation, effectively transporting the particles to just outside the resonance zone. Nevertheless, even in the confinement phase the 1/3 ringlet is slowly gaining L_z. In practice the ringlet density peak is not moving but the ringlet slowly leaks particles outward, carrying the excess angular momentum (see Fig. 3, upper row). This elongates the life-time of the ringlet compared to that estimated from the rate of angular momentum gain, but it still implies eventual dispersal.

A possible mechanism leading to a practically permanent stabilization  would be to have satellite(s) located outside the ringlet. Since the actual confinement of the ringlet would still be provided by the 1/3 SOR perturbation, a broad range of satellite distances/masses would be expected be able to prevent the spreading of the tail particles. The lower row of Fig. 3 provides an example, with a small satellite outside the 1/3 resonance. In the absence of 1/3 perturbation such a satellite prevents the outward spreading and creates a sequence of spiral density perturbations at its inner first order resonances (here with m=5,6,7,8). When combined with 1/3 SOR perturbation (lower right frame; the satellite was added after 100,000 revolutions) the tail particles are pushed back to the main body of the ringlet, which now remains confined both from inside and outside. In the example shown, the increase in ringlet L_z has in fact been been reverted to a slow decrease, which presumably would be stabilized when the ringlet has moved a little closer to 1/3 resonance. Thus, the location of the ringlet is still governed by the 1/3 SOR

Acknowledgments. BS thanks the French ANR “ROCHE" for support

 

 

Fig. 1 - Simulations of 1/3 resonance with a μ=0.1 mass anomaly on the surface of spherical central body. Upper row shows non-colliding test particles: the angular momentum L_z  distribution (left) is not affected and a gap forms in instantaneous particle positions (right) due large eccentricities. The middle row shows colliding particles in the absence of perturbation, experiencing rapid viscous spreading. In the lower row both collisions and perturbation are included, leading to accumulation of particles at the resonance with synchronized eccentricities, followed by the formation of confined ringlet. Simulations use 30,000 particles, with  R=200 meters when scaled to Chariklo system, yielding initial optical depth τ=0.06. The coefficient of restitution ε_n=0.1. In the Cartesian projections the width of the ring and the deviations of the center-line from mean distance are exaggerated by a factor of five for better viewing. Note that inclusion of central body elongation (e=0.20 for Chariklo) would have no noticeable effect on the behavior.

 

Fig. 2 - A survey of 1:3 resonance simulations with R=25m-800m and mass-anomaly μ=0.003 -0.1. The optical depth τ=0.015. Frames in the left show the evolution of L_z distribution (duration of simulations vary 20,000 -200,000 central body revolutions). In the right the filled/open symbols distinguish between simulations leading to resonance accumulation/dispersal. The black curve indicates the accumulation threshold, following the scaling of viscous and resonance excitation timescales for a second-order resonance. Shaded region extrapolates the accumulation region to τ∼1.

 

 

 

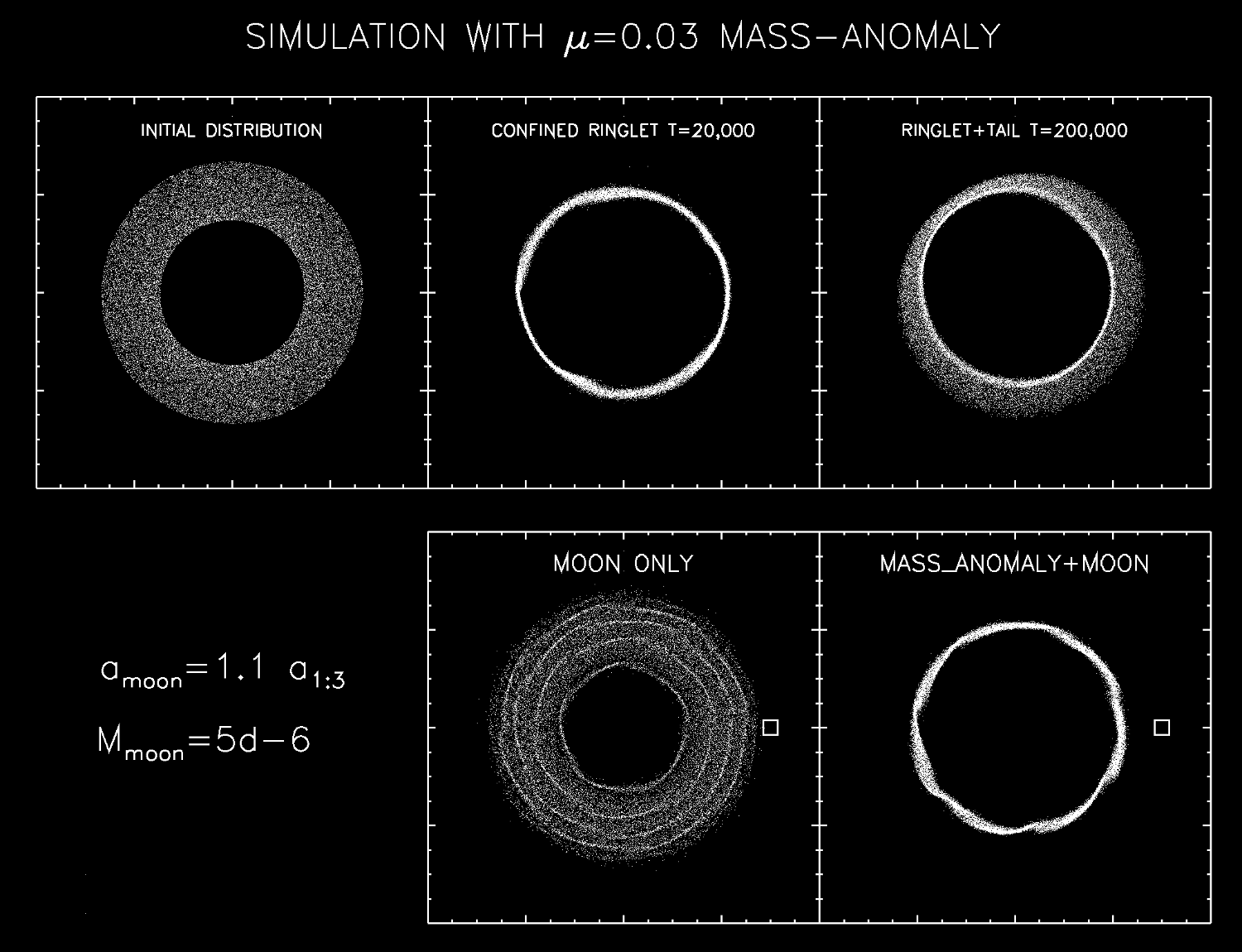
Fig. 3 - Upper row: long term evolution of  1/3 SOR ringlet with  μ=0.03;  Note the eventual slow leaking of particles from the ringlet, which maintains sharp edges.  Lower row: effect of satellite on the ringlet, with mass 5 10^-6 relative to central body, located 10% outside the 1/3 SOR. Without 1/3 perturbation the ring spreads inward and spiral density perturbations develop at first order resonances with the moon. When satellite is added to a simulation with a 1/3 SOR ringlet (after 100,000 revolutions), the leaking of ringlet is prevented. In the figure the ring widths and deviations are expanded by a factor of 10; also the satellite position has been shifted for clarity.