Polar motion of Venus and Envision measurements

Context

The first estimation of Venus’ moment of inertia (Margot et al. 2021) paves the way for addressing geophysical questions such as the estimation of size of its core. In parallel, three exploration missions have been selected to study Venus for the next decade. Notably, one of EnVision mission objectives is a geophysical investigation of Venus (ESA 2023).

Examining the rotational dynamics of an object can offer clues about the nature and properties of its interior. The motion of the spin axis of a planet can be described with respect to the fixed celestial sphere (precession and nutation) or with respect to the planetary surface itself (polar motion), both motions bringing complementary clues about the planet’s interior. The precession motion of the spin axis of Venus has been recently measured for the first time, albeit with an uncertainty too large to help constrain interior models (Margot et al. 2021), while its polar motion has yet to be measured.

Aim

We develop a model of polar motion for Venus, and we study the influence of geophysical parameters such as the moment of inertia and the size of the core, in anticipation of its future exploration by the EnVision mission.

Model

A polar motion solution of a triaxial planet is obtained through the Euler-Liouville equation accounting for the solar torque, the rotational and tidal deformations of a viscoelastic mantle, and the varying inertia and angular momentum of the atmosphere. We compute the frequency of the free motion (Chandler wobble) and its characteristic damping time, as well as the frequencies and amplitudes of the forced motion.

The solar torque may affect the Chandler Wobble of Venus because of its slow rotation. On the other hand, whereas deformations due to the centrifugal potential (pole tide) significantly decreases the Chandler frequency of the Earth, they are negligible in the case of Venus due to its largely non-hydrostatic shape.

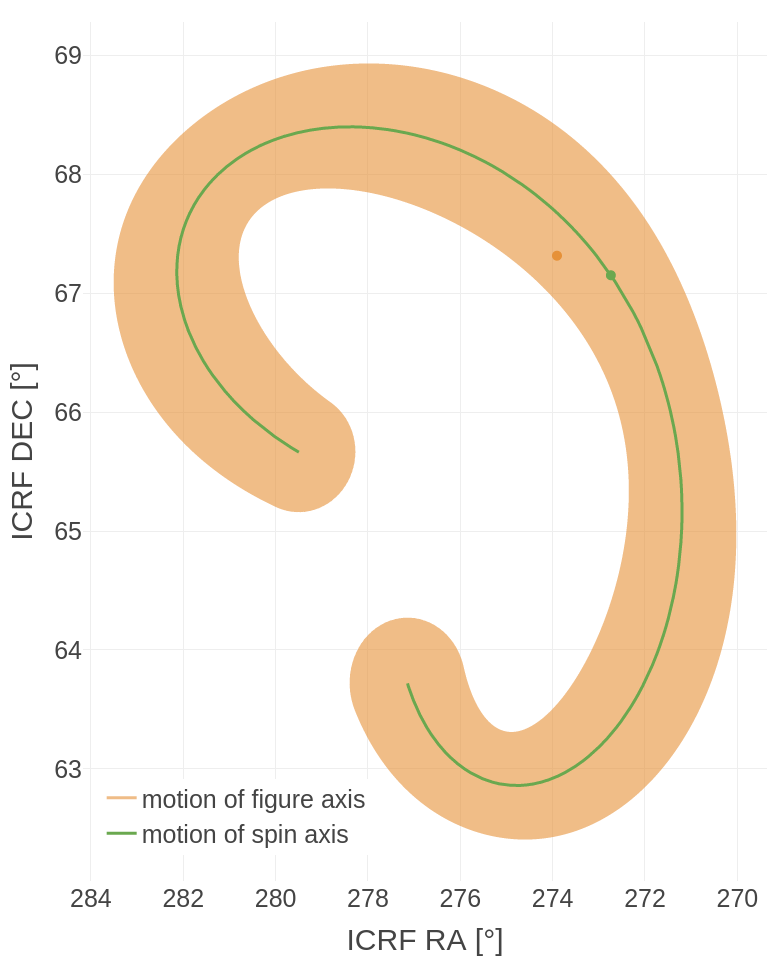
Figure 1 - Motions in the ICRF of the spin axis of Venus (in green) and the figure axis (polar moment of inertia axis, in orange) for a 30000 years period centered on J2000. The spin axis moves clockwise, and the figure axis circles anti-clockwise around the spin axis with a period of 243 days. Colored dots indicate axes orientations at epoch J2000. RA is right ascension, DEC is declination.

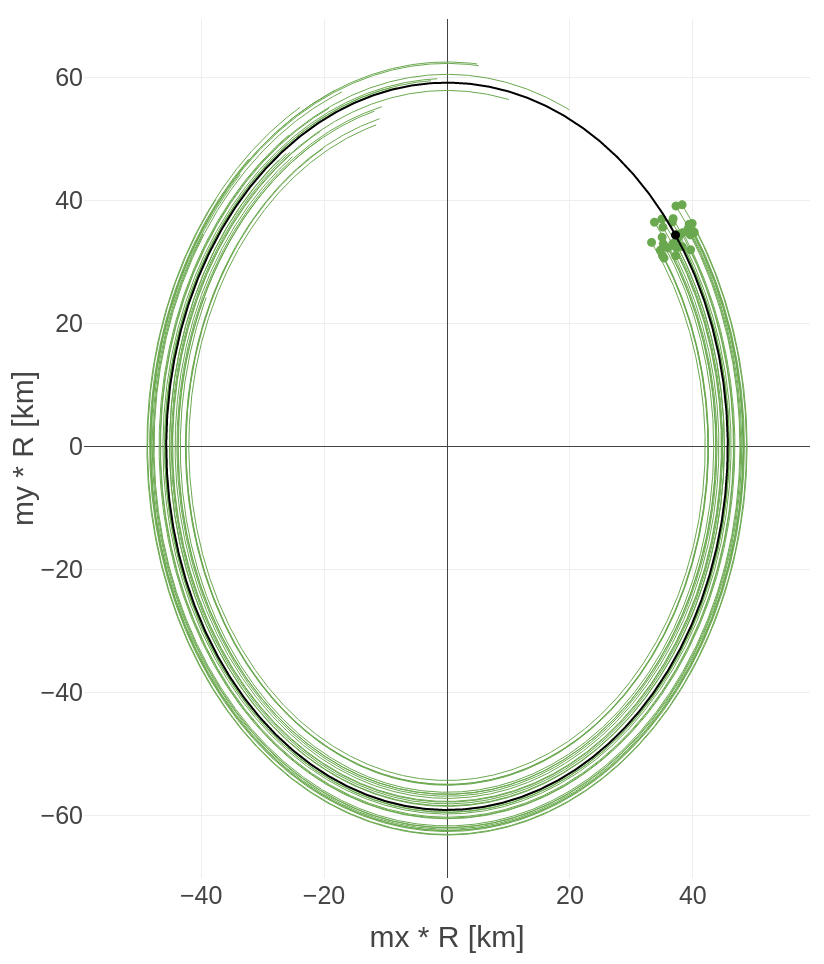
Figure 2 - Polar motion of the spin axis of Venus, in the figure frame (principal moments of inertia axes) for a 15000 years period beginning at epoch J2000. mx and my are the equatorial components of the unit spin vector, R is the mean radius of Venus. The 30 different solutions (in green) are the results of sampling from the uncertainty distributions for Venus’ gravity field and moment of inertia. The nominal solution is plotted in black.

Future measurements

The EnVision orbiter will use its radar to image the surface of Venus with a resolution of tens of meters over a few years. The polar offset derived from its gravity field (Konopliv et al. 1999) would suggest that the polar motion of Venus would be measurable by EnVision, on top of the precession motion.

By tracking the position of surface control points in inertial space, one can constrain the rotation model of a planet. For Venus, it has been achieved with Magellan radar imaging for a uniform rotation model (Davies et al. 1992), and has been studied for a precession model (Cascioli et al. 2021). In this work we will analyze the potential recovery of the combined precession and polar motion of Venus ; the measurement of these rotational dynamics will contribute to refining models of the planet's internal structure.

References

Margot, JL., Campbell, D.B., Giorgini, J.D. et al. (2021) Spin state and moment of inertia of Venus. Nat Astron 5, 676–683. https://doi.org/10.1038/s41550-021-01339-7

ESA (2023), “EnVision, Understanding why Earth’s closest neighbour is so different”, Definition Study Report (Red Book), ESA document reference.
https://www.cosmos.esa.int/documents/10892653/0/EnVision+Red+Book_ESA-SCI-DIR-RP-003.pdf

Konopliv, A. S., Banerdt, W. B., & Sjogren, W. L. (1999). Venus gravity: 180th degree and order model. Icarus, 139(1), 3-18. https://doi.org/10.1006/icar.1999.6086

Davies, M. E., Colvin, T. R., Rogers, P. G., Chodas, P. W., Sjogren, W. L., Akim, E. L., ... & Zakharov, A. I. (1992). The rotation period, direction of the north pole, and geodetic control network of Venus. Journal of Geophysical Research: Planets, 97(E8), 13141-13151. https://doi.org/10.1029/92JE01166

Cascioli, G., Hensley, S., De Marchi, F., Breuer, D., Durante, D., Racioppa, P., ... & Smrekar, S. E. (2021). The determination of the rotational state and interior structure of Venus with VERITAS. The Planetary Science Journal, 2(6), 220. https://doi.org/10.3847/PSJ/ac26c0