A numerical method to determine bulk thermal conductivity of randomly packed particle beds

Introduction: The Hayabusa2 mission [1] investigated the near-Earth asteroid (162173) Ryugu by remote sensing and in-situ measurements. A comprehensive analysis of the asteroid’s thermophysical properties [2] revealed a discrepancy between results obtained at the asteroid and measurements performed on the returned samples. While it has been proposed that the low thermal conductivities observed in-situ would be caused by the high porosity of boulders in the Ryugu [3], it has been hypothesized that thermal properties may be scale dependent [4]. The latter, for example, be caused by thermal fatigue induced cracks as a result of diurnal temperature forcing.

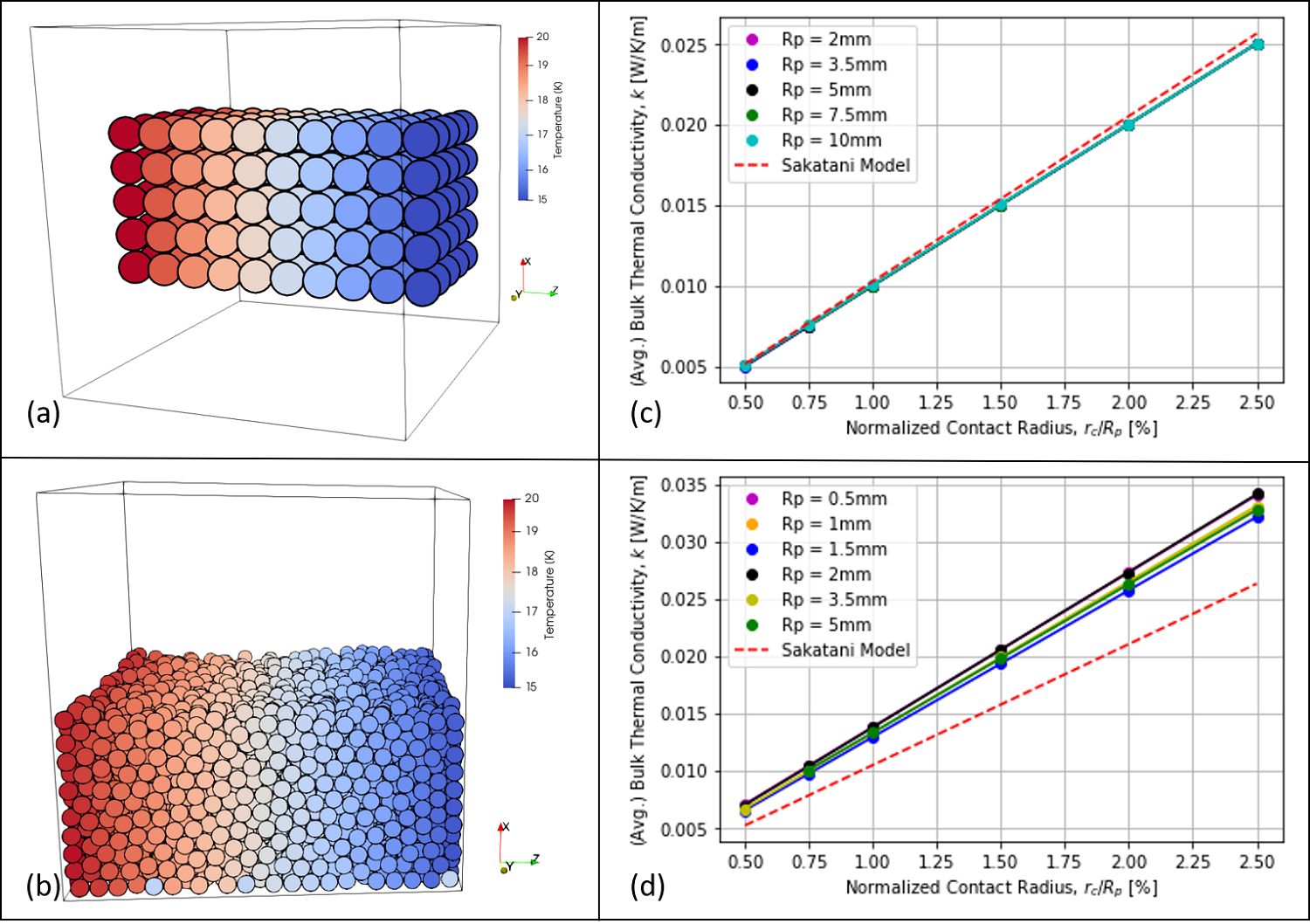
Fig. 1: Results of simulating heat flow through beds of monodisperse particles driven by a temperature gradient between two plates. (a) Temperature distribution within a particle bed in simple cubic packing, where color represents particle temperatures going from red (hot) to blue (cold). (b) Same as (a), but for a random packing of particles. (c) Thermal conductivity as a function of contact radius normalized to particle radius for a suite of particle beds in simple cubic packing with particle diameters between 0.5 mm (pink) to 5 mm (green). (d) Same as (c), but a random packing of particles.

 

Modeling: We aim to investigate the thermophysical properties of carbonaceous material using numerical simulations. To this end, we simulate heat transfer in a particle bed where individual particles are connected through sintering bonds at the particle necks [4]. We use the open source software LIGGGHTS®-PUBLIC package [5] which implements the discrete element method to calculate interactions between particles. Fig. 1 shows two such particle beds, with 1a showing a simple cubic packing of particles, while 1b represents a randomly packed bed of particles. The beds are subjected to temperature boundary conditions on the left and right side of the computational domain, while keeping the other boundaries adiabatic.

Once the simulation reaches a quasistatic state, we determine the flux through the bed by evaluating flow through particle layers perpendicular to the temperature gradient. Layers are spaced equally through the bed between hot and cold boundaries. We use the particles which intersect (or touch) the planes to determine the heat flux through them. For each layer m and particle i, heat flow into the particle (and thus into the plane) is determined by summing up all the heat flow contributions from neighboring particles j, considering only the net influx of heat (in thermal equilibrium, the total flow through layer is zero). Assuming particle thermal conductivity k_p as well as contact radii r_c between particles to be constant, heat flow  into a particle is given by

Qm,i = Σj max(Tm,j - Tm,i, 0)·((kp,i·kp,j)/(kp,i+kp,j))·rc

(1)

 

where T_m,i is the temperature of particle i. The term on the right-hand side corresponds to the thermal conductance between particles  and  in the units of [W/K]. Heat flow Q_m into layer  is then given by summing all contributions from particles in that layer

Qm = Σi Qm,i

(2)

 

and average flow through the entire packing (of m layers) is then given by

Q =(Σi Qi )/m

(3)

 

Bulk thermal conductivity k_bulk of the particle bed can now be calculated using Fourier’s law given by the area A of the bounding plates, their separation Δz, and the temperature gradient ΔT between them:

kbulk = (Q/A)·(Δz/ΔT)

(4)

 

This approach accounts for the statistical variation of heat flow inside the randomly packed particle bed and we have run benchmark tests using a simple cubic packing as well as randomly packed particle bed varying particle radius R_p and radius of contacts r_c.

Results: Fig. 1 shows the results of calculating heat transport through particle beds in a simple cubic packing (fig. 1c) and through randomly packed beds (fig. 1d). Thermal conductivities have been determined as delineated and the results have been compared to an analytical model that parameterizes the particle contacts in terms of particle bed porosity and the average particle coordination number [6]. Assuming smooth particles of radius R_p, and thermal conductivity k_p, the bulk thermal conductivity k_bulk,m of the particle bed is given by [6]

kbulk,m = (4/π2)·kp ·(1-φ)C·(rc/Rp)

(5)

 

where φ and C are porosity and average coordination number for the particle bed, respectively. For the benchmark, particles have been assumed to be monodisperse to facilitate the comparison, but the method is readily extended to arbitrary grain-size distribution.

Fig. 1c shows thermal conductivity as a function of normalized contact radius for particle sizes between 2 and 10 mm assuming a simple cubic packing. Results of the numerical simulations are in excellent agreement with the analytic model and bulk thermal conductivity is a function of normalized contact radius only, as would be expected from Eq. (5). Results for the random packing are shown in Fig. 1d, and we observe a slight deviation from the model which remains to be investigated in further detail.

Outlook: Having established a method to calculate bulk thermal conductivity in randomly packed particle beds, we will now continue to study the influence of porosity on bulk thermal conductivity. To this end, we will use the sphere placer algorithm developed by [7] to generate particle beds with predefined porosities. The algorithm employs random ballistic deposition of particles and is able to achieve packing porosities between 42% and 85%. As the particle beds thus generated are not in mechanical equilibrium, we will introduce predefined bonds between particles or use cohesion between particles to stabilize the beds. Bulk thermal conductivity of the packing can then be determined as a function of porosity to further investigate the relationship between sample porosity and its thermal conductivity.

 References: [1] S. Watanabe et al. Space Science Reviews 208, 1 (2017), p. 3–16. [2] K. Otto et al. Earth, Planets and Space 75, 1 (2023), p. 51. [3] M. Grott et al. Nature Astronomy, 3, 971-976 (2019). [4] B. Agrawal et al. LPSC 2024 Abstract No. 1471. [5] C. Kloss et al. Progress in Computational Fluid Dynamics, An Int. J. 12, 2/3 (2012). [6] N. Sakatani et al. AIP Advances 7, 015310 (2017). [7] L. Klar et al. Granular Matter 26, 59 (2024)