Distance metrics for dynamical association of meteors

Meteor showers, originating from disruptions of comets or asteroids, offer insights into the composition and dynamics of the Solar System. However, distinguishing sporadic meteors from those belonging to specific meteoroid streams remains a challenge.

This study evaluates four orbital similarity criteria within a five-dimensional parameter space (D_SH, D_D, D_H, and ϱ₂ [1-4]) for dynamical associations, using the CAMS database as a benchmark. Additionally, we assess various Machine Learning distance metrics with two vectors: ORBIT (based on heliocentric orbital elements) and GEO (based on geocentric observational parameters). We test the Top-k agreement and compute the optimal cut-offs for distinguishing sporadic events by analyzing the ROC curve using Youden’s J statistic [5].

Our findings indicate that the sEuclidean metric paired with the GEO vector demonstrates superior performance compared to other metrics and the D-criteria, achieving the highest Top-1 accuracy of 87.06%. Among the D-criteria, D_SH is the most effective for Top-1 accuracy at 86.23%, while ϱ₂ leads in both Top-5 (95.67%) and Top-10 (97.93%) accuracy. The Bray-Curtis metric, when combined with the ORBIT vector, consistently outperforms other distance metrics and the D_D criterion across all Top-k tests, achieving Top-1, Top-5, and Top-10 accuracies of 83.96%, 94.10%, and 96.61%, respectively. D_D exhibits an opposite trend to other D-criteria when evaluated against distance metrics with the GEO vector. In general, ϱ₂ appears to be the most comparable to distance metrics using the GEO vector and is the most compatible with both GEO and ORBIT vectors simultaneously.

The mean accuracies for Top-1, Top-5, and Top-10 tests are 83.7%, 93.6%, and 96.2%, respectively, with the highest accuracies achieved using the GEO vector (85.1%, 93.4%, 95.9%) rather than the ORBIT vector (81.8%, 93.2%, 95.9%). This suggests that geocentric parameters provide a more robust basis than orbital elements for meteor dynamical association.

The sEuclidean metric, when used with the GEO vector, achieves the highest overall accuracy (84.34%) and Matthews correlation coefficient (phi) of 0.6464, closely followed by Cityblock and Bray-Curtis metrics. Among the D-criteria, D_SH distinguishes itself with a phi of 0.6400, translating to an accuracy rate of 84.17% in separating the background, while D_D emerges as the least effective, with a phi of 0.5877 and an accuracy of 81.87%. In the context of the ORBIT vector, Cityblock takes the lead with a phi of 0.6359 and 84.04% accuracy, closely followed by Bray-Curtis and Euclidean metrics.

Excluding the Cosine metric, all distance metrics associated with the GEO vector surpass the D-criteria in phi when differentiating the meteoroid background. Despite the generally lower performance of the ORBIT vector, various distance metrics still exceed certain D-criteria in effectiveness. Optimal cut-offs for all D-criteria and distance metrics are provided, based on the CAMS database classification. See Table 1. The complete details of this work can be found in [6]

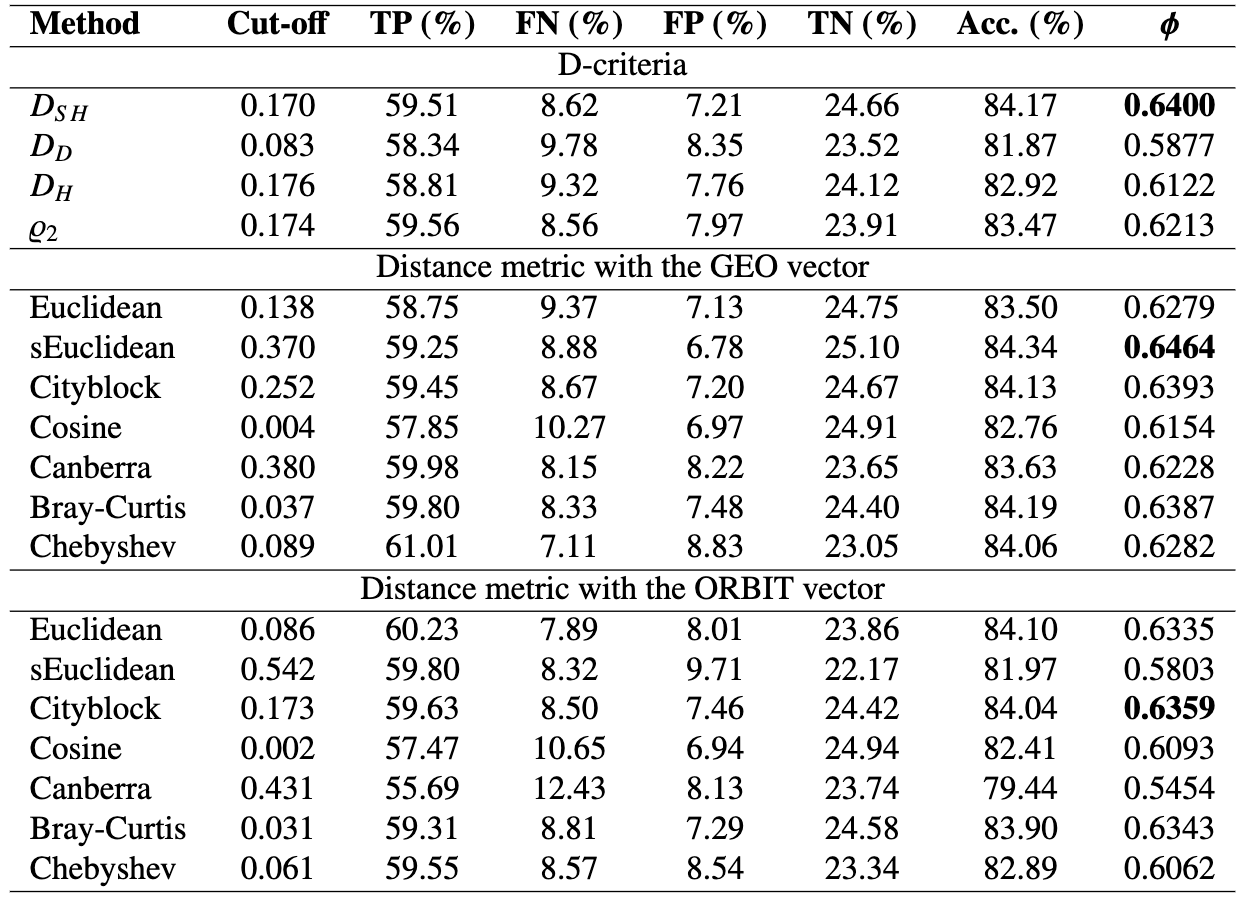
Table 1. Threshold, accuracies, and Matthews correlation coefficients for different D-criteria and distance metrics in the CAMS database taking into account the sporadic and associated events.

In conclusion, this study reveals that Machine Learning distance metrics can rival or even outperform specifically tailored orbital similarity criteria for meteor dynamical association.  

 

References

[1] Southworth, R. B., & Hawkins, G. S. (1963). Smithsonian Contributions to Astrophysics, 7, 261–285.

[2] Drummond, J. D. (1981). Icarus, 45(3), 545–553.

[3] Jopek, T. J. (1993). Icarus, 106(2), 603–607. 

[4] Kholshevnikov, K. V., Kokhirova, G. I., Babadzhanov, P. B. et al. (2016). Monthly Notices of the Royal Astronomical Society, 462(2), 2275–2283.

[5] Youden, W. J. (1950). Cancer, 3(1), 32–35.

[6] Peña-Asensio E., & Sánchez-Lozano J.M. (2024). Advances in Space Research, in press, https://doi.org/10.1016/j.asr.2024.05.005.