Impact of the subsurface magma ocean on tidal dissipation and the Love numbers

Introduction

Io, one of the Galilean moons, is the most active volcanic body in our Solar System. The volcanic activity is driven by tidal heating due to its orbital resonance with Europa and Ganymede. The tidal response of a planetary body depends on its size, internal structure, and the orbital parameters. Dissipation can occur both in the solid and liquid parts of the body. In the solid layers, dissipation depends on the shear modulus and anelastic behavior of the rock which strongly depends on the melt fraction, while in the liquid layers, the dissipation depends on the viscosity and can be strongly affected by the Coriolis force. The existence of a liquid magma ocean on Io is a subject of debate. Earlier studies of tidal heating of Io assume that most of the tidal heat is generated in a partially molten layer beneath the lithosphere or in deeper mantle (1–4). Recently, Miyazaki and Stevenson (5) suggested the possibility of a magma ocean on the top of a partially molten layer. In this study, we compute the tidal dissipation and the gravitational response of Io with a magma ocean. Assessing Io’s tidal response and its implications for the internal structure can help to understand the processes in the tidally heated exoplanets.

Method

Most of the previous models of the tidal response of a planetary body with a subsurface liquid ocean were obtained by solving two-dimensional Laplace tidal equations (LTE). LTE models assume that the radial flow in the ocean is negligible compared to the lateral flow and the ocean thickness is small compared to the radius of the body (e.g., 6–8). In this study, we model the tidal response of Io by solving the three-dimensional Navier-Stokes equations. Unlike previous 3D models (9, 10), our model self-consistently links the flow in the liquid ocean with the viscoelastic deformation of the solid layers (11).

The thickness of the magma ocean is varied from 100 m to 10 km. The viscosity of the magma ranges from 100 Pa s (hot mafic magma) to 10⁷ Pa s (low-temperature magma with solid crystals (10)). The lithosphere above and the mantle below the ocean are assumed to behave as a Maxwell viscoelastic solid, and the magma ocean is treated as a Newtonian viscous liquid. The density structure of Io is set to satisfy the constraints of the total mass and moment of inertia factor, and the upper lithosphere is chosen to be 30 km thick.

Tidal dissipation and the Love numbers

We show that the tidal flow produced by our model gives a wide range of tidal heating patterns (Figure 1). In all the models, the tidal heating is concentrated in the equatorial regions. Some models show a distinct pattern that is independent of longitude. The purely zonal character of the dissipation pattern is unusual in the context of eccentricity tides. This heat distribution has a noteworthy correspondence with the geological map of Io (see Figure 2 in (13)).

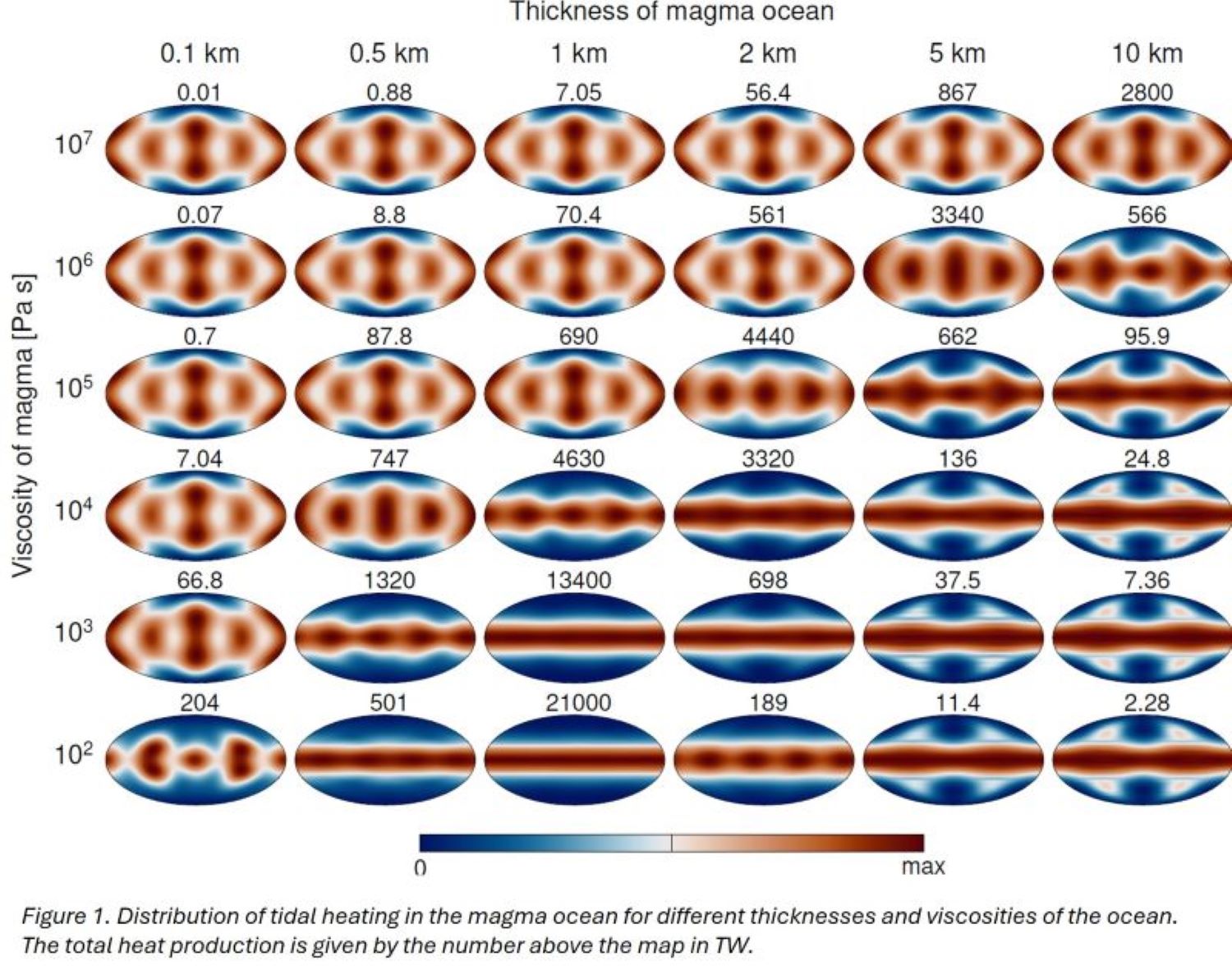
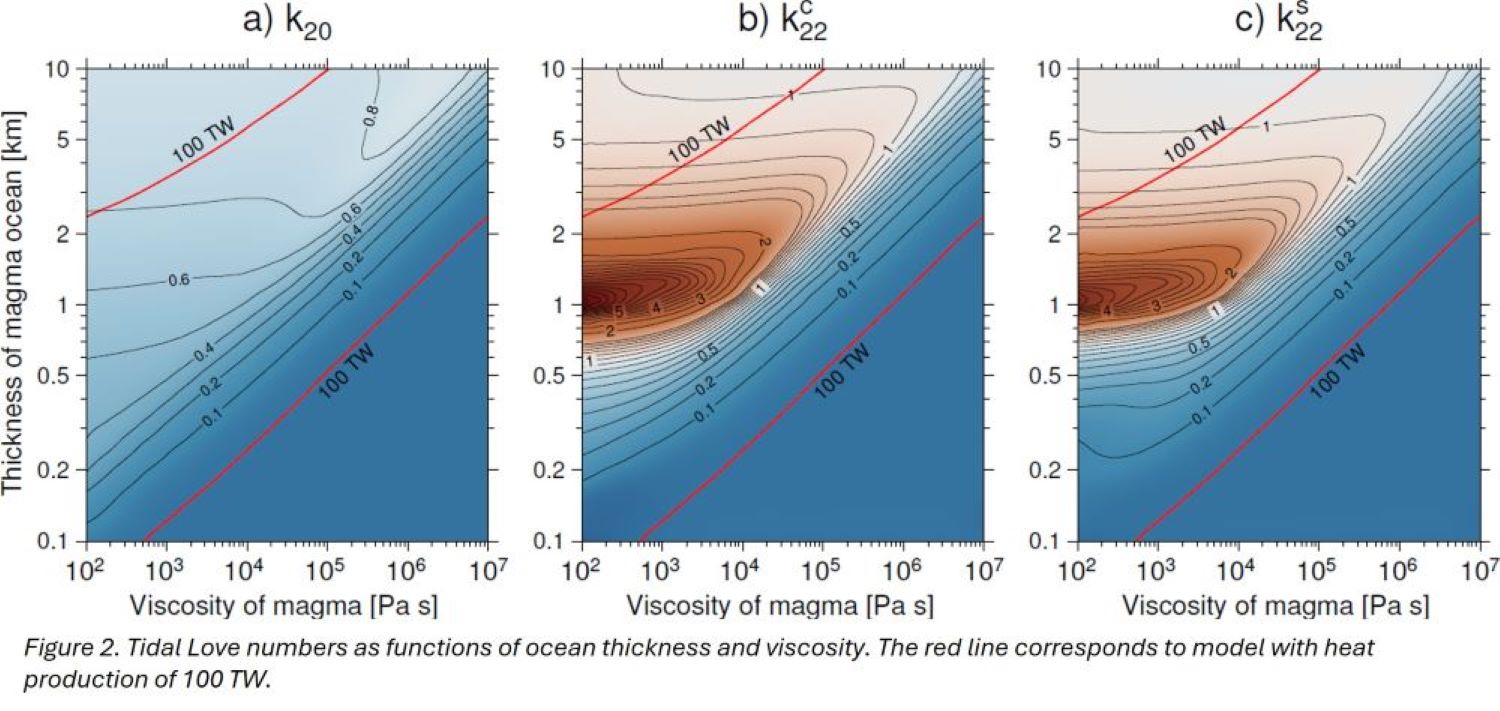
The question of whether there exists a magma ocean on Io can be answered by analyzing time variations of the gravity signal of Io (1). In the previous models, the tidal Love number is computed with a hydrostatic magma ocean (e.g., 2). In here we present that tidal response of Io can be strongly affected by dynamic flow in the magma ocean. Unlike the case with solid body tides, in the presence of a magma ocean, degree-2 Love numbers can depend on the harmonic order due to strong Coriolis effect. In Figure 2, we present the Love numbers as a function of ocean thickness and viscosity (for detailed definitions of the Love numbers see (13)). The Love number for harmonic order 0 is increasing with the ocean thickness, reaching a maximum of 0.85, while the Love numbers for harmonic order 2 are strongly affected by the Coriolis term and reach a maximum that is 10 times larger.

 Conclusions

Tidal heating given by our model confirm the results of previous studies (e.g., 7) but our model gives a broader set of heat flux patterns. The heat distribution depends on the viscosity and thickness of the magma ocean and is concentrated in the equatorial regions. This is consistent with new observations by Juno spacecraft which suggest that hot spots at lower latitudes emit more energy than the hot spots in the polar regions (14).

The tidal Love numbers can be strongly affected by the dynamics of the ocean. If the tidal heating occurs in the present-day magma ocean (100 TW, red lines in Figure 2), then the degree-2 Love numbers are either less than 0.1 or greater than 0.7 depending on the ocean thickness and viscosity.  The Love numbers are insensitive to the presence of a thin ocean which should be considered in the future analysis of Io’s gravitational response.

 Acknowledgements

B.A. acknowledges the support form the Charles University project SVV 260709.

References

1. C. J. Bierson, F. Nimmo, J. Geophys. Res.: Planets. 121, (2016), doi:10.1002/2016JE005005.

2. M. Kervazo et al., Astron. Astrophys. 650 (2021), doi:10.1051/0004-6361/202039433.

3. T. Steinke et al., Icarus. 335 (2020), doi:10.1016/j.icarus.2019.05.001.

4. M. N. Ross, G. Schubert, Icarus. 64, (1985), doi:10.1016/0019-1035(85)90063-6.

5. Y. Miyazaki, D. J. Stevenson, Planet. Sci. J. 11, (2022), doi:10.3847/PSJ/ac9cd1.

6. M. Beuthe, Icarus. 280, (2016), doi:10.1016/j.icarus.2016.08.009.

7. R. H. Tyler et al., Astrophy. J. Supp. S. 218, (2015), doi:10.1088/0067-0049/218/2/22.

8. I. Matsuyama et al.,, Icarus. 312, (2018), doi:10.1016/j.icarus.2018.04.013.

9. M. Rovira-Navarro et al., Icarus. 321, (2019), doi:10.1016/j.icarus.2018.11.010.

10. J. Rekier et al., J. Geophys Res Planets. 124, (2019), doi:10.1029/2019JE005988.

11. B. Aygün, O. Čadek, J. Geophys. Res.: Planets. 128 (2023), doi:10.1029/2023JE007907.

12. A. R. Philpotts, J. J. Ague, Principles of Igneous and Metamorphic Petrology Cambridge University Press, Cambridge, UK, 2nd edition., 2009.

13. B. Aygün, O. Čadek, Geophys. Res. Lett. 51 (2024), doi:10.1029/2023GL107869.

14. A. G. Davies et al., Nat. Astron. 8, (2024), doi:10.1038/s41550-023-02123-5.