3D Surface Radiative Transfer Model via Raytracing for Airless Bodies with the Application to Lunar Craters and Possible Ice-Stability

Introduction

The Moon has many permanently shadowed regions (PSRs) inside of craters at the poles, which are only illuminated by indirect (reflected) sunlight and thermal radiation because of the small solar incidence angle and obliquity. That is why the terrain of the poles strongly influences the temperature profile of the regolith. These exceptionally cold PSRs are areas that are most likely to harbor water ice (Vasavada 1999; Watson et al. 1961) and are therefore of interest to future landing missions. One example is the NASA CLPS-10, which carries ESA’s PROSPECT instrument, which, using the Drill, will sample the lunar surface up to 1 m depth with the aim to detect volatiles including water ice if present (Boazman et al. 2023).

The temperature of the regolith can be described as a function of depth using a one-dimensional thermal model. In craters, it is necessary that the incident radiation on each surface element is accurately considered as a boundary condition, as this depends strongly on the surrounding topography. The crater walls can block radiation, but they can also reflect it.

Coupling the surface boundary condition determined in this model with a thermal model from Bürger et al. (2024) for the regolith layers allows conclusions to be drawn about the depth and position of water ice in such craters and surface temperatures measured remotely by instruments such as Diviner (Paige et al. 2010).

Method

In our model, the topography of the region of interest is then transformed into a mesh of triangles using Delaunay triangulation. For each facet, the conservation of energy applies, which states that the radiated heat must be equal to the direct absorbed solar radiation, plus the direct absorbed IR radiation emitted by all other facets, plus the absorbed radiation (solar and IR) reflected by all other facets, plus the heat flux from the sub-surface. Reflections in the visible and IR range are taken into account for all orders. The sun is approximated as a point source and its position is calculated using SPICE. Whether a facet is seen by the sun is determined using ray tracing. The proportion of radiation transmitted from one facet to another is proportional to the view factor, also known as the form factor, and the associated albedos and emissivities. Previous similar models, e.g. Potter et al. (2023), Vasavada (1999) or Gläser et al. (2019), usually use only angle-independent albedos. However, laboratory measurements (Foote et al. 2020), thermal models for the lunar surface (e.g. Keihm 1984; Vasavada et al. 2012; Hayne et al. 2017; Bürger et al. 2024) and a model that estimates the albedo from the lunar noontime surface temperatures as a function of latitude (Feng et al. 2020) show that the albedo is indeed angle-dependent, which is why this effect is also taken into account, as some other models already do (King et al. 2020).

Initial Results

As a first step and as a verification method, we neglect the sub-surface heat flow, i.e. the thermal model, and compare the numerical raytracing model for a constant solar incidence angle (equilibrium case), constant albedo and a perfectly bowl-shaped crater (see fig. 1) with the analytical solution of Ingersoll et al. (1992). We find a good agreement between these two models.

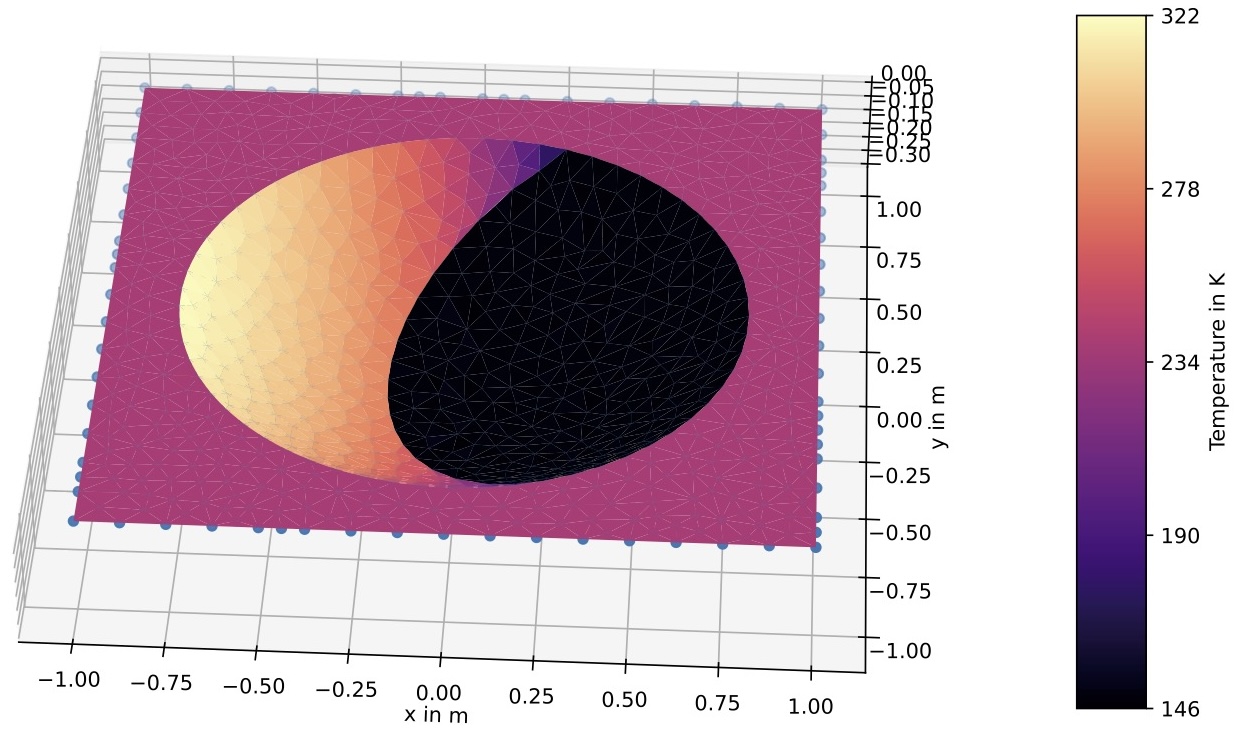
Figure 1: Equilibrium surface temperature distribution of a perfectly bowl-shaped crater for a solar incidence angle of e_⊙ = 15° (emissivity = 0.99, albedo = 0.3).

In the next step, the model was equipped with an angle-dependent albedo. As expected, the albedo models used always cause the temperature in the crater to drop, as less radiation is absorbed at higher angles of incidence. The extent to which the temperature drops depends heavily on the albedo model and can be up to 30 K.

Applying the model to real craters with realistic topography produces surface temperature maps for a specific position of the sun (again in the equilibrium case, see fig. 2) or over the course of a lunar day (e.g. for maximum temperatures) while also neglecting sub-surface heat flow.

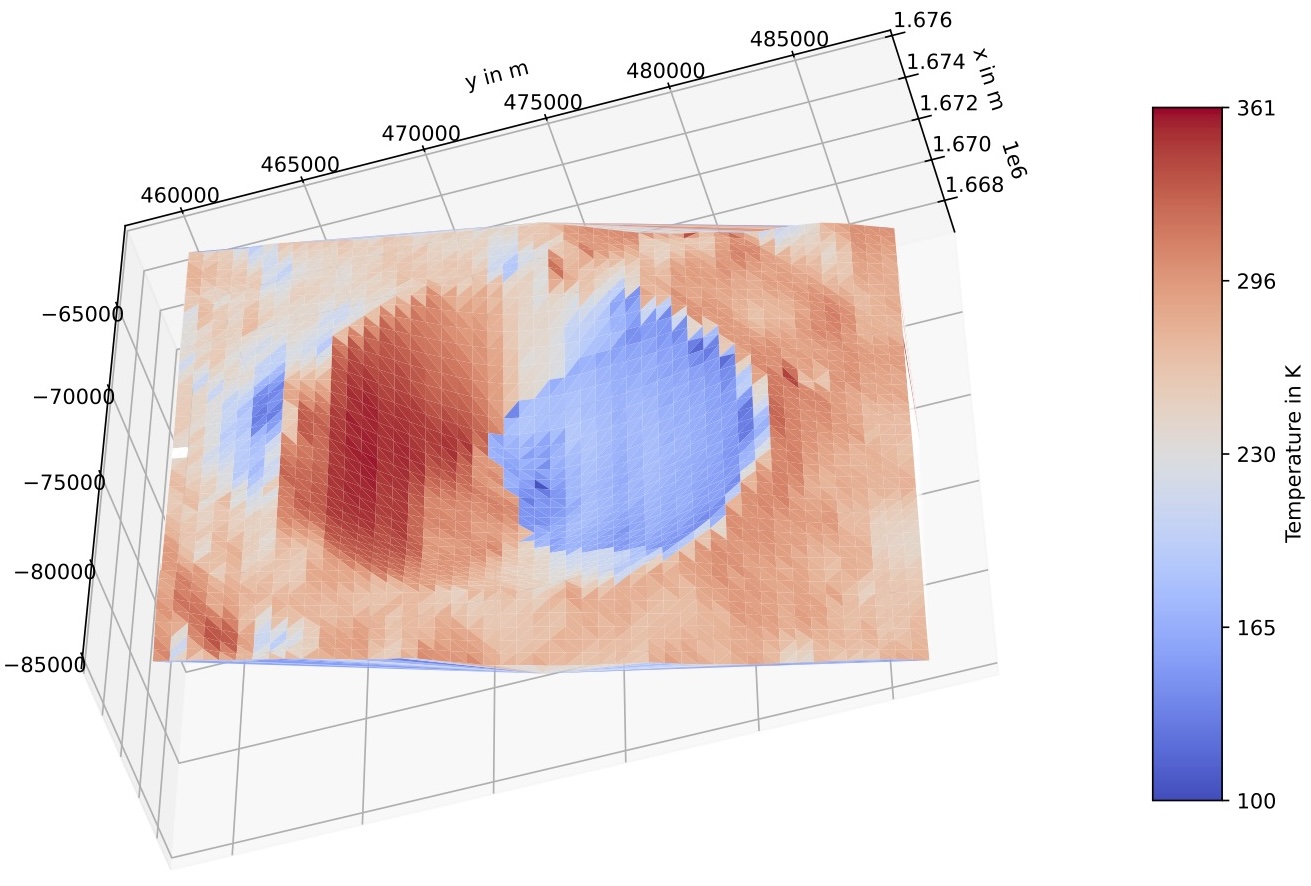
Figure 2: Equilibrium surface temperature distribution for solar incidence angle of e_⊙ = 20.07° with angle-dependent albedo (Feng et al. 2020) for the Theon Junior crater.

Outlook

In the future, the sub-surface heat flow will be taken into account by coupling the thermal model of Bürger et al. (2024) with the surface boundary condition determined here to obtain more accurate surface temperatures and temperatures of the deeper layers of the regolith.

The primary objective is then to determine the water ice stability as a function of location and depth. This will provide us with valuable constraints for upcoming missions and instruments searching for water ice at the lunar South pole, such as the Prospect drill, in order to identify suitable drilling targets.

References

Boazman, S. J. et al. (2023). 54th LPSC. Vol. 2806. LPI Contributions, 2019. Bürger, J. et al. (2024). JGR Planets 129.3. Feng, J. et al. (2020). JGR Planets 125.1, e2019JE006130. Foote, E. J. et al. (2020). Icarus 336, 113456. Gläser, P. et al. (2019). A&A 627, A129. Hayne, P. O. et al. (2017). JGR Planets 122.12, 2371–2400. Ingersoll, A. P. et al. (1992). Icarus 100.1, 40–47. Keihm, S. J. (1984). Icarus 60.3, 568–589. King, O. et al. (2020). P&SS, 182, 104790. Paige, D. A. et al. (2010). Science, 330.6003, 479–482. Potter, S. F. et al. (2023). J. Comput. Phys., X 17, 100130. Vasavada, A. (1999). Icarus 141.2, 179–193. Vasavada, A. R. et al. (2012). JGR Planets 117.E12.