The tidal response of Ganymede with a realistic compressible dynamic ocean

Introduction

Understanding the internal structure of Ganymede and the ongoing processes in its interior is critical for assessing its formation, evolution and the potential habitability of its subsurface ocean. While the observations of Ganymede’s auroral oval oscillations confirmed the presence of a salty, electrically conductive ocean¹, the structure of the hydrosphere remains unconstrained². The Juice mission will provide unique constraints on Ganymede’s hydrosphere by determining the tidal Love numbers, which are sensitive to the ice shell thickness and its mechanical properties³, but also to the composition and dynamics of  ocean^4,5,6.

In this study, we present a new 3D numerical tool, Oceanus, developed for calculating the Love numbers of realistic planetary interiors. Oceanus considers previously neglected physical effects, namely the compressibility, inertial and the Coriolis forces in the ocean. Our aim is to predict the Love numbers of Ganymede that Juice is expected to measure. This study consists of two parts: we first quantify the effects of compressibility and the dynamical flow in the ocean due to eccentricity tides. We then investigate the tidal perturbations due to moon-moon interactions⁴ and the resulting ocean’s response.

3D modeling of the ice-ocean dynamic response using Oceanus

Oceanus computes the tidal response of a planetary body by solving the 3D linearized Navier-Stokes equations in time domain. Unlike previous models that are used to compute the tidal response, Oceanus accounts for compressibility and tidal flow in liquid layers. It provides complete information about the tidally induced gravity signals, predicting the degree 2 Love number separately for orders 0 and 2 (e.g., k₂₀ and k₂₂ )^4,6. For eccentricity tides, Love numbers remain constant during a tidal cycle, while for moon–moon tides, they vary in time and are expressed as the sum of a time-averaged component and an oscillatory part. The Love numbers for moon-moon tides differ from those in frequency domain.

We describe the interior of Ganymede with five layers: a solid ice Ih shell, a viscous liquid ocean, a solid high-pressure ice, a solid mantle, and a liquid core. The interior profiles are defined by two parameters: the ice shell thickness b (in the range of 10—152 km), and the ocean composition C. We consider three compositions corresponding to the NaCl solution of 0 wt.%, 5.8 wt.%  and 11.7 wt.% . For each case, the reference density, bulk modulus, and shear modulus profiles are computed consistently from the pressure-temperature conditions using the SeaFreeze thermodynamic representation⁷. The mantle and core densities are fixed to 3500 and 8000 kg/m³, respectively, and their radii are set to match Ganymede’s observed mass and moment of inertia. Both the silicate mantle and the iron core are assumed to be incompressible and the tidal flow in the core is neglected. The solid layers are assumed to behave as an elastic or Maxwell viscoelastic body and the ocean is treated as a Newtonian fluid with a viscosity of 100 Pa s.

Response to eccentricity tides

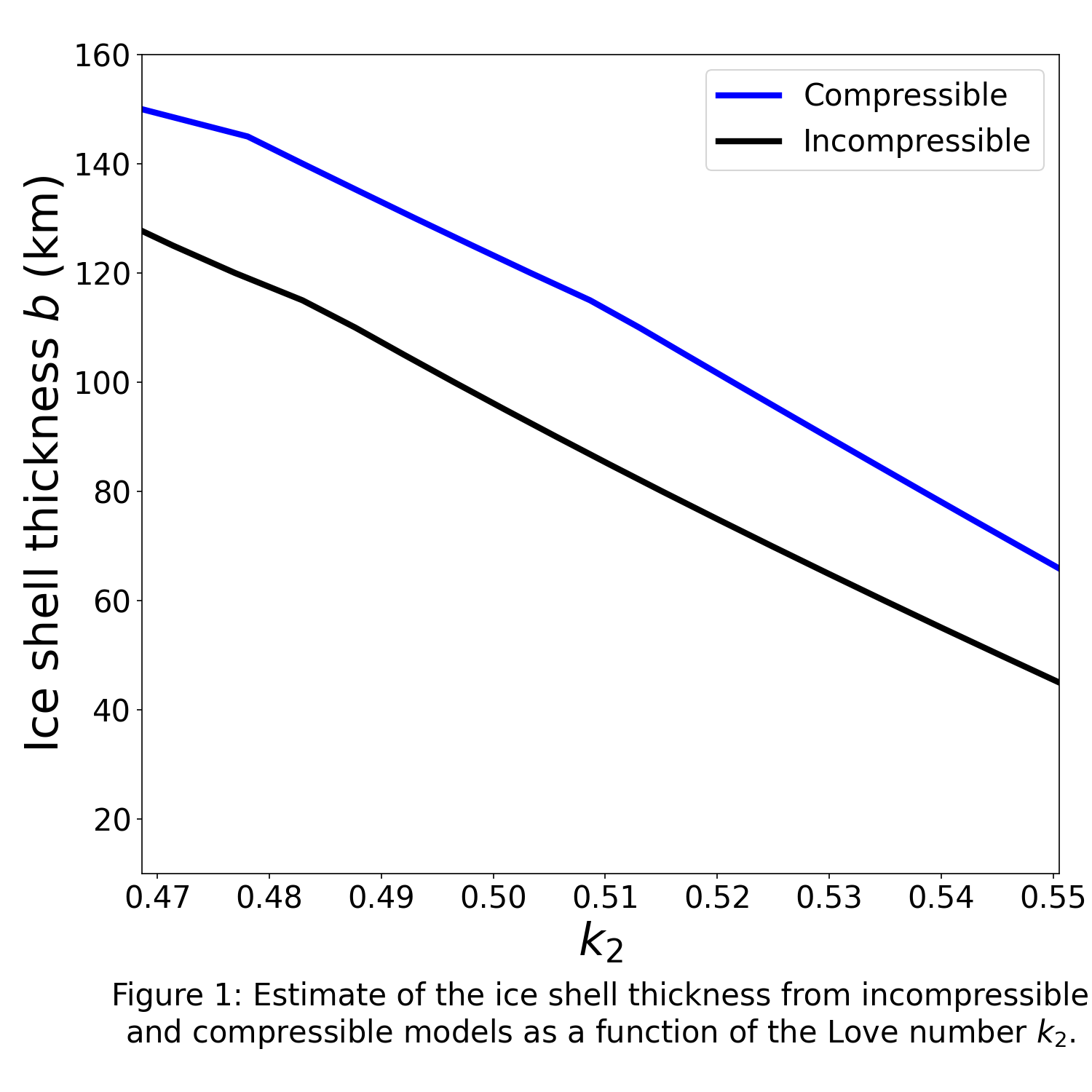
Our results show that the compressible Love numbers of Ganymede range from 0.41 to 0.58 depending on the hydrosphere's structure. The value of k₂ increases with decreasing ice shell thickness and increasing salt concentration. The difference in the Love numbers between the incompressible and compressible models ranges from 2% to 6% (Figure 1). For a given Love number, the estimated ice shell thickness can differ by 20 to 30 km between compressible and incompressible models. For thick oceans (>10 km, b<145km), the tidal flow in the ocean leads to a decoupling between the order 0 and 2 Love numbers by up to 7%. For thin oceans (d<10 km, b>150km), this difference increases to 10%.

Response to moon-moon tides

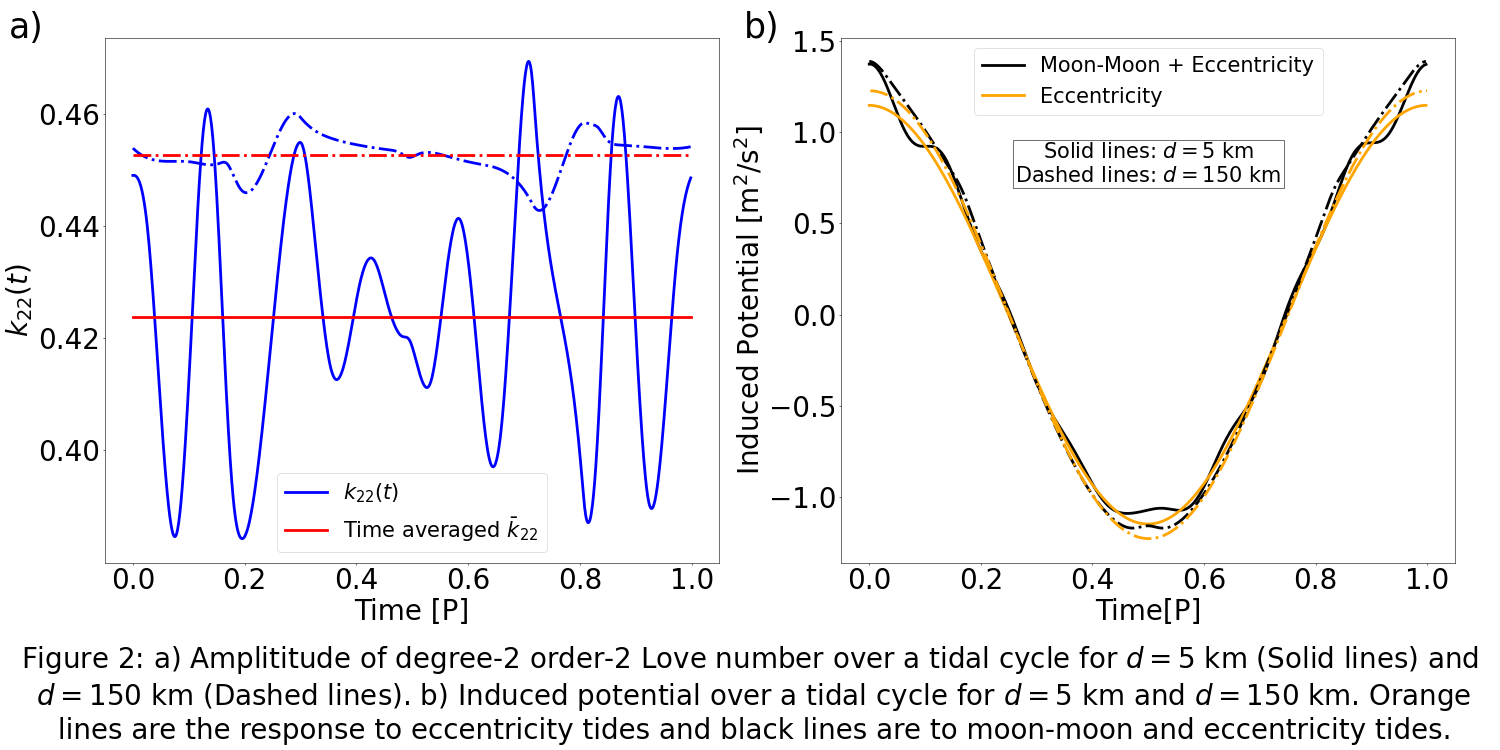
We consider the tidal interaction with Io and Europa. The time-averaged Love number differs by 2% from the Love number obtained from the eccentricity tides for both thin and thick ocean cases (Figure 2b). While the average response is similar, the behavior of the oscillatory part depends on the ocean thickness. For thin oceans, k₂ shows high-frequency oscillations and its instantaneous value can vary by nearly 10%, whereas for thick oceans, the oscillations are dampened, and the deviations are about 2-3% (Figure 2a). Our results indicate that the response to the moon-moon tides are smaller than what was previously anticipated⁸, but remains detectable by 3GM experiment.

Conclusions

Depending on the ocean concentration of NaCl and the ice shell thickness, we predict the Love numbers of Ganymede to vary from 0.41 to 0.58. Our computations show that using incompressible models can lead to errors of up to 30 km in the estimated ice shell thickness. While the dynamics of a thin ocean (d<10 km) significantly alters the gravitational signal, the effects of the tidal flow in thicker oceans are weaker, but larger than the expected accuracy of Juice/3GM experiment⁹. The expected accuracy is 0.01% on the time-averaged k₂⁹, while in most of our simulated cases k₂₀ and k₂₂ differ by a few percent, and up to 10% for thin ocean. In response to moon-moon tides, k₂ can vary during a tidal cycle by 2% for thick oceans and up to 10% for thin oceans, while its time-averaged value remains close to the Love number for eccentricity tides.

Acknowledgments

This project is supported by ANR-2020-CE49-0010, from CNES for the preparation of the Juice mission, Charles University project SVV 260825, and the Czech Science Foundation project No. 25-16801S.

References

[1] Saur et al., 2015, JGR: Spa. Sci. 120, 1715–1737

[2] Vance et al., 2018, JGR.: Planets 123, 180-205

[3] Kamata et al., 2016, JGR.: Planets 121, 1362–1375

[4] Hay et al., 2022, JGR: Planets 127, e2021JE007064

[5] Aygün & Čadek, 2024, GRL 51, e2023GL107869

[6] Aygün & Čadek, 2025, Icarus 436, 116567

[7] Journaux et al., 2020, JGR: Planets 125, e2019JE006176

[8] De Marchi et al. 2022, Icarus 386, 115150

[9] Cappuccio et al. 2020, Plane. & Spa. Sci. 187, 104902