Ice rheology and tidal Love numbers of Uranus’s moons.

The major moons of Uranus (Miranda, Ariel, Umbriel, Titania and Oberon) might hide subsurface oceans underneath their ice shells, that is why they are scientific targets of great relevance. This fact and others make “the Uranus Orbiter and Probe (UOP) the highest-priority new Flagship mission for initiation in the decade 2023–2032”, as stated in the Planetary Science and Astrobiology Decadal Survey 2023-2032 [1]. Several recent studies have already investigated the possibility that these bodies may host a fluid layer below their surfaces [2,3,5]. A work by [7] showed that the presence or absence of a subsurface ocean would have a strong effect on the expected value of the tidal k₂ Love number (LN), and that tidal deformations of these moons are mostly influenced by the characteristics of their ice shells. However, as stated in [8], the lack of experimental data on the flexural behavior of ice at tidal-like frequencies hinders the accurate attribution of an appropriate rheological model. For this reason, this work focuses on highlighting the importance of the rheological characterization of the ice shell of these bodies, and its influence on the determination of the values of the LNs k₂, h₂, and l₂. These are a-dimensional coefficients that depend on the internal structure of a planetary body and describe the response of the planet (or satellite) to tidal forcing. The vertical LN h₂ can be measured through altimetric techniques, while the potential LN k₂ can be assessed with radio science experiments. Instead, the measurement of the horizontal LN l₂ requires instrumentation that relies on land-based antennas, such as VLBI, making its estimate extremely complicated for the case of distant worlds. The first estimates of the LN k₂   for the major moons of Uranus may be available in the next future: this quantity can be of great importance to further understand the interior structure of these moons and can provide significant hints on the presence of liquid oceans and their thermal status. In this work, through a series of forward models, we test the sensitivity of LNs to several internal parameters, i.e. the presence of a deep ocean, the rheology of the outer ice shell and the density structure of the moons.

 

Starting from Uranus’ moons masses and radii, we build a set of models which explore a range of possible rheological layering, including both the presence and absence of an ocean. For the rheological description of the ice shell, we adopted different creep laws (Andrade, Burgers, Sundberg-Cooper), already largely used in the literature to describe icy moons (see e.g. [6,8,9]). While the ocean is modeled as a Newtonian fluid, the inner core is assumed to be viscoelastic. For each model we compute the three LNs together with other parameters like the tidal quality factor Q, and the tidal lag φ, and we investigated the extent to which these quantities vary with changes in the ice shell properties (thickness, rheology, viscosity and rigidity).  The computations of LNs are carried out using ALMA [7], a numerical LNs calculator.  

 

In Fig. 1 we show the results obtained for Titania, considering an orbital frequency of 8.7 days. The use of different rheological models for the description of the ice shell has a strong effect especially on the imaginary part of the k₂  LN, a quantity directly connected to the tidal dissipation:  being able to quantify this variability is then important to correctly assess the effects and consequences of tidal deformations on these bodies. Furthermore, as found in other studies (see e.g. [2] and [7]), we verified that models with a subsurface ocean have a k₂  which can differ by an order of magnitude from the one of equivalent models without it (Fig. 1). Hence, it remains to be determined, once the number of flybys is known, whether and for which moons the measurement accuracy will be sufficient to distinguish between the two scenarios. Then, we found that both k₂  and l₂  are sensible to the presence of subsurface ocean, but a measure of l₂  would be more effective to constrain its depth and thickness (Fig. 2, right). However, due to the nature of the horizontal displacements associated to the LN l₂, obtaining its estimate may remain challenging in the near term.

 

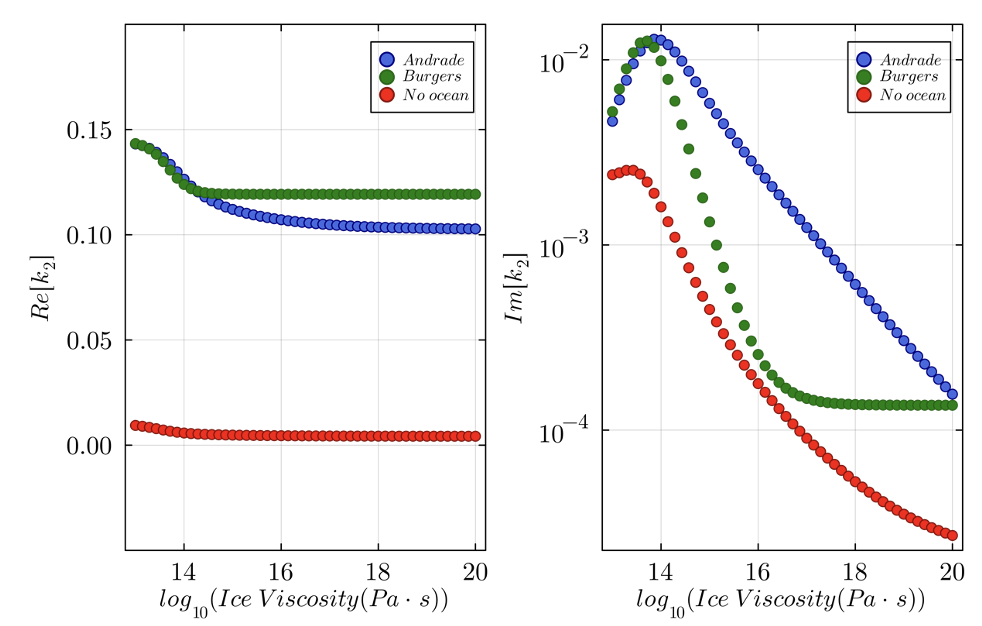
Fig. 1: Real and imaginary part of the k₂ LN as a function of the viscosity of the ice shell. “Andrade” and “Burgers” indicate 4-layer models including an elastic ice lid, a viscoelastic ice layer described by Andrade or Burgers rheology, a fluid ocean of 10 km, and an inner, viscoelastic core. The red dots represent a model equivalent to the “Andrade” one where the oceanic layer is replaced by ice. The presence of the ocean has a strong effect on the k₂  value.

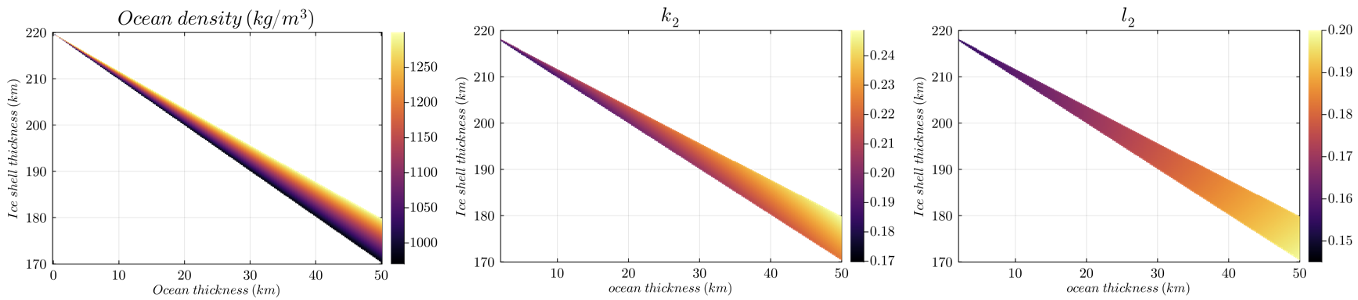
Fig. 2: The panel on the left depicts the ocean density (kg/m³) as a function of the ocean width and ice shell width (km). Next, we have respectively the LNs k₂  and l₂. The horizontal LN l₂ seems to be proportional to the ocean thickness and depth.

 

ACKNOWLEDGEMENTS: GS, GM, DM and AC are grateful to the Italian Space Agency (ASI) for financial support through Agreement No. 2024‐5‐HH.0

 

References:

[1] National Academies of Sciences, Engineering, and Medicine. "Origins, Worlds, and Life: Planetary Science and Astrobiology in the Next Decade." (2023).

[2] Castillo‐Rogez, J., et al. (2023) JGR: Planets 128.1.

[3] Ćuk M. et al. (2020) Planet. Sci. J. 1 22.

[4] Hemingway, D. J., and F. Nimmo (2024) GRL 51.

[5] Gevorgyan, Y., et al. (2020) Icarus 343.

[6] Melini, D., et al. (2022) GJI 1502-1517.

[7] Petricca, F. et al. (2025) JGR: Planets 130.4.

[8] Tobie, G., et al. (2025) Sp. Sci. Rev. 221.1 (2025): 1-5.