Oral presentations and abstracts
The goal of this session is to cover numerical simulations and relevant laboratory investigations related to the Small Bodies (comets, KBOs, rings, asteroids, meteorites, dust), their formation and evolution, and the instruments of their exploration. This session is specially focused on the interdisciplinary approach in the development of models (formal descriptions of physical phenomena), experiments (on ground and in micro-gravity), and mathematical simulations (computational methods and algorithms of solution) of various astrophysical phenomena: (i) dusty gas cometary atmospheres; (ii) volcanic activity on icy satellites (e.g. Enceladus and Io); (iii) planetary body formation (e.g. via pebbles growth), and planetesimal dynamics.
This session will include an introduction and discussion of new and/or existing laboratory studies in simulated space-like environments and models, experimental techniques, computational methods that can address the results of analytical,experimental and numerical analysis (with respect to computational methods and algorithms of solution) on the above described studies.
Abstracts on thermophysical evolution models of small bodies interiors as well as on the modeling of atmosphere and exosphere are welcome.
Session assets
Grain growth in protoplanetary disks is the first step towards planet formation. One of the most important pieces in the grain growth model is calculating the collisional velocity between two grains induced by the turbulent motion of the gas. The collisional velocities in previous works are obtained based on the assumption that the turbulence is hydrodynamic with the Kolmogorov power spectrum. However, realistic protoplanetary disks are magnetized, and turbulent motions can be induced by the magneto-rotational instabilities (MRI).
To understand the impact of MRI turbulence on grain growth, we carry out 3D MHD simulations of the MRI as well as driven turbulence, for a range of physical and numerical parameters. Figure 1 illustrates the magnetic field structure in one of the MRI simulations. We investigate two fundamental parameters of the turbulence that can have large impacts on grain collision velocities, the kinetic energy spectrum and the turbulence autocorrelation time.
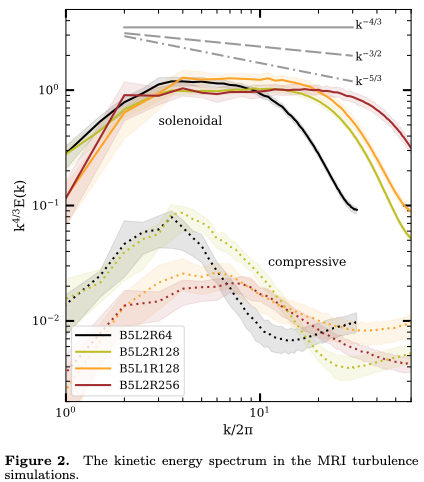
We find that the convergence of the turbulence α-parameter does not necessarily imply the convergence of the energy spectrum. The MRI turbulence is largely solenoidal, for which we observe a persistent kinetic energy spectrum with a -4/3 slope, shallower than the -5/3 slope in the Kolmogorov turbulence (Figure 2). The same is obtained for solenoidal driven turbulence with and without magnetic field, over more than 1 dex near the dissipation scale. This power-law slope appears to be converged in terms of numerical resolution, and to be due to the bottleneck effect. The kinetic energy in the MRI turbulence peaks at the fastest growing mode of the MRI. In contrast, the magnetic energy peaks at the dissipation scale. The magnetic energy spectrum in the MRI turbulence does not show a clear power-law range, and is almost constant over approximately 1 dex near the dissipation scale. The turbulence autocorrelation time is nearly constant at large scales, limited by the shearing timescale, and shows a power-law drop at small scales, with a slope close to -1, steeper than that of the eddy crossing time.
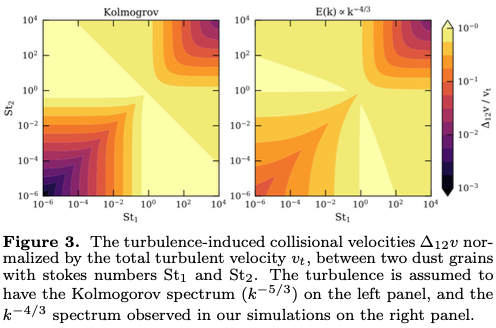
The deviation from the standard picture of the Kolmogorov turbulence can have a significant impact on the grain collisional velocities. Figure 3 shows the collisional velocities in Kolmogorov turbulence and turbulence observed in the simulations. For small grains that are well coupled to the gas, the collisional velocities can vary by orders of magnitude across different turbulence models. To understand the dust growth in protoplanetary disks, better computational techniques are needed to achieve the large dynamical range necessary for resolving the turbulence spectrum in the future.
Reference:
Gong M., Ivlev A. V., Zhao B., Caselli P., 2020, ApJ, 891, 172
How to cite: Gong, M., Ivlev, A., Zhao, B., and Caselli, P.: Impact of magneto-rotational instability on grain growth in protoplanetary disks, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-316, https://doi.org/10.5194/epsc2020-316, 2020.
INTRODUCTION
In the trans-Neptunian region a relatively large fraction of minor bodies are found to exist as mutually bound binary pairs. The binary fraction varies for different dynamical classes and is highest for the Cold Classicals, which are dynamically unexcited planetesimals generally found at 39 < a < 48 AU, with estimates of up to 30% of the Cold Classicals being binaries (Noll et al. 2008).
A distinct feature of the observed trans-Neptunian binaries is that they often have components that are of a similar size. These components also have similar optical colours which likely indicates similar surface compositions. Furthermore, the binary orbits span a range of separations but it is not uncommon for them to be found on wide (abin > 0.05 RHill) dynamically fragile orbits. The binary orbit inclinations range from prograde to retrograde, with ~80% of the known trans-Neptunian binaries having prograde orbits. The discovery of the bi-lobate nature of the Cold Classical contact binary 2014 MU69 Arrokoth, with its similar size and colour lobes, indicates that this object is likely the end state of a previously separated trans-Neptunian binary (Stern et al. 2019).
Previous work (Nesvorný et al. 2010) has shown that the formation of planetesimals via gravitational collapse is a promising mechanism that can reproduce the unique properties of the trans-Neptunian binaries. We assume that a slowly rotating cloud of pebbles grows in the protoplanetary disk, for example via the streaming instability. Eventually this cloud collapses under its own self gravity and merging collisions lead to the rapid growth of ~100 km planetesimals. Conservation of angular momentum in the rotating cloud means that these planetesimals are frequently formed as a binary pair. For a given binary orbit the angular momentum is maximised by forming a system with similar mass components. Additional work (Nesvorný et al. 2019) has shown that the inclination distribution of binary planetesimals formed via streaming instability and gravitational collapse is a good match for the observed inclination distribution.
METHODS
We performed N-body simulations of the gravitational collapse of a pebble cloud using the Symplectic Epicyclic Integrator within the REBOUND package (Rein & Liu 2012). The pebble cloud was approximated by a rotating uniform spherical distribution of 105 computational particles. The radii of the computational particles was inflated in order to replicate the collisional behaviour of a high number density pebble cloud. Collisions were detected when particles were found to be overlapping and we considered the timestep required to ensure that collision detection was robust. We performed a deep search for systems of gravitationally bound particles and tested their stability. For all systems produced we investigated the population characteristics of their mass and orbital parameters.
RESULTS
Our results demonstrate that gravitational collapse is an efficient producer of bound planetesimal systems, and frequently forms multiple bound systems per cloud. On average there were ~1.5 bound systems produced per cloud in the mass range we have studied. As well as the large equal-sized binaries which were the focus of previous work, we found that gravitational collapse can produce a range of systems such as massive bodies with small satellites and low mass binaries with a high mass ratio. The binaries with equal-size components have bound orbits with low inclinations and low to moderate eccentricity, similar to the observed trans-Neptunian binaries. The additional binaries with dissimilar-sized components or low system mass span a large range of inclinations and eccentricities. Our results disfavour the collapse of the high mass clouds in our dataset (Mc = 1.8e21 kg), as they form large equal-sized binaries that are not observed (figure 1). This finding is in line with reported upper mass limits of clouds formed by the streaming instability. Gravitational collapse of low mass clouds (Mc ≤ 4.2e18 kg) can create binary systems with similar total mass and mass ratio as the contact binary Arrokoth (figure 1). Furthermore, we find that collisions between planetesimals growing in such a collapsing cloud should be gentle enough to preserve a bi-lobed structure, which further supports the gravitational collapse origin of Arrokoth.
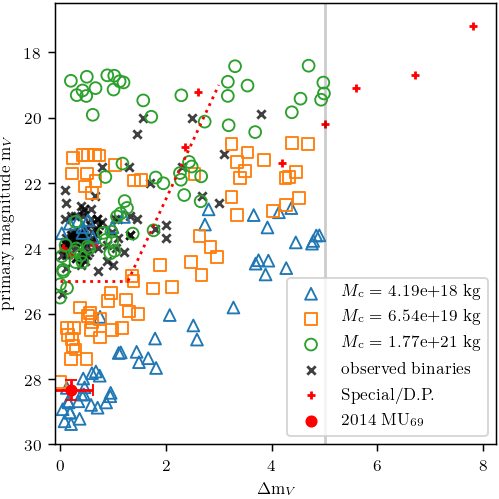
Figure 1. Primary V band magnitude against magnitude difference between primary and secondary components for binaries produced by gravitational collapse simulations. Marker colour and shape indicates the initial cloud mass. The vertical line indicates the mass ratio cut off of m2/m1 ≥ 10−3 in the orbit search algorithm. The observed trans-Neptunian binaries from Grundy (2019) are shown as black 'x's. We represent 'special cases' and dwarf planets as red '+'s. The red circle with error-bars represents how Arrokoth would appear if its components could be separately resolved. An approximate empirical detection limit (Noll et al. 2008) and a lower magnitude limit of 25 are shown as red dotted lines.
REFERENCES
Grundy, W. (2019). Mutual Orbits of Binary Transneptunian Objects. Retrieved December 2nd, 2019, from online webpage website: http://www2.lowell.edu/users/grundy/tnbs/
Nesvorný, D., Youdin, A. N., & Richardson, D. C. (2010). Formation of Kuiper Belt Binaries by Gravitational Collapse. The Astronomical Journal, 140, 785–793. https://doi.org/10.1088/0004-6256/140/3/785
Nesvorný, D., Li, R., Youdin, A. N., Simon, J. B., & Grundy, W. M. (2019). Trans-Neptunian binaries as evidence for planetesimal formation by the streaming instability. Nature Astronomy, 3, 808–812. https://doi.org/10.1038/s41550-019-0806-z
Noll, K. S., Grundy, W. M., Chiang, E. I., Margot, J.-L., & Kern, S. D. (2008). Binaries in the Kuiper Belt. In The Solar System Beyond Neptune (pp. 345–363). Tucson: The University of Arizona Press.
Rein, H., & Liu, S. F. (2012). REBOUND: An open-source multi-purpose N-body code for collisional dynamics. Astronomy and Astrophysics, 537, A128. https://doi.org/10.1051/0004-6361/201118085
Stern, S. A., Weaver, H. A., Spencer, J. R., Olkin, C. B., Gladstone, G. R., Grundy, W. M., … Zurbuchen, T. H. (2019). Initial results from the New Horizons exploration of 2014 MU69, a small Kuiper Belt object. Science, 364(6441). https://doi.org/10.1126/science.aaw9771
How to cite: Robinson, J. E., Fraser, W. C., Fitzsimmons, A., and Lacerda, P.: Investigating Gravitational Collapse of Pebble Clouds to form Trans-Neptunian Binaries, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-891, https://doi.org/10.5194/epsc2020-891, 2020.
Migration of planetesimals to the Earth from the zone beyond the orbit of Jupiter was considered by us e.g. in [1-3]. References to papers of several other authors on migration of bodies to the Earth were presented in [1]. In [1] we considered migration of planetesimals from the zone from 4.5 to 12 AU. In [2-3] migration of planetesimals with initial semi-major axes a0 of their orbits between 5 and 40 AU was considered. Below I also consider migration of planetesimals with a0 between 3 and 5 AU to the Earth.
Migration of planetesimals under the gravitational influence of 7 planets (from Venus to Neptune) or 5 planets (from Venus to Saturn) was calculated with the use of the symplectic code from [4]. The. In each variant of the calculations, the initial values of semimajor axes of orbits of planetesimals varied from amin to amax=amin+da, the initial eccentricities were equal to eo, and the initial inclinations equaled to eo/2 rad. Orbital elements of the migrated planetesimals were recorded in computer memory with a step of 500 years. Based on these arrays of orbital elements, I calculated the probabilities of collisions of planetesimals with the Earth, and for some runs I also calculated the probabilities of collisions of the planetesimals with other terrestrial planets, the Moon and their embryos. The calculations were made similar to those in [1-3, 5-7].
In the series of calculations considered in [2-3], da=2.5 AU, and amin took values from 2.5 to 40 AU in increments of 2.5 AU. The initial eccentricities equaled to 0.3 or 0.05. In each calculation variant, 250 planetesimals were considered, but for the same values of amin, da, and eo, several (up to 8) calculation variants were performed. So the total number of considered planetesimals for a set with fixed values of amin, da and e0 could reach 2000. Some calculations were made for da=0. In the recent series of calculations, da=0.1 AU, and amin took values from 3.0 to 4.9 AU in increments of 0.1 AU. For this series of calculations, the initial eccentricities equaled to 0.02 or 0.15. In Figs. 1-6 for several series of calculations, we present the values of 106pE, where pE is the probability of a collision of a planetesimal with the Earth. In Figs. 1-2 the values of 106pE are presented for time intervals equaled to 1, 10 and 100 Myrs. For other figures usually greater time intervals (up to 2 Gyrs) were considered (until the values of pE finished to grow with time). For variants presented in Figs. 1-4 and 6, the gravitational influence of 7 planets (from Venus to Neptune) was taken into account. For runs for Fig. 5, Uranus and Neptune were excluded.
At amin≤10 AU, the value of pE calculated for a run with 250 bodies could vary hundreds of times for different calculation variants with the same values of amin, da and eo. Such difference was earlier found for calculations of migration of Jupiter-crossing objects [5-6]. One among several hundreds or among thousands of such objects moved in Earth-crossing orbits during millions or even tens of millions of years, and the probability of a collision of such object with the Earth was greater than that for hundreds or even thousands of other objects. The values of pE in Figs. 1-6 vary from a value less than 10-7 to values of the order of 10-3, but they are mainly between 10-6 and 10-5. On average, pE is smaller for greater amin. There were no runs with pE>10-5 at amin≥12.5 AU or for the runs without Uranus and Neptune. pE≤1.5×10-6 at e0=0.3 and amin≥27.5 AU. In Figs. 1-2, the fraction of runs with pE>10-5 at e0=0.15 is greater than at e0=0.02. In some runs there was a considerable growth of pE after 10 Myr. At da=0.1 AU and e0=0 or e0=0.15, there were more runs with pE>2×10-5 for 3.2≤amin≤4.1 AU than for other values of amin.
Calculations showed that the amount of material delivered from beyond Jupiter’s orbit to the Earth could exceed the mass of the Earth’s oceans if the total mass of planetesimals beyond Jupiter’s orbit was about 200 Earth masses. Some (perhaps 1/3) of this material consisted of water and volatile substances. The mass of the substance delivered to the planet to the mass of the planet for Mars was approximately two times greater than for Earth, and such relations for Mercury and Venus were slightly larger than for Earth. The total mass of planetesimals migrating from beyond the orbit of Jupiter and colliding with the Moon was 16 or 17 times less than the total mass such bodies collided with the Earth.
The work was carried out as a part of the state assignments of the Vernadsky Institute of RAS.
References:
[1] Marov M.Ya., Ipatov S.I., Delivery of water and volatiles to the terrestrial planets and the Moon // Solar System Research, 2018, 52, 392-400. https://arxiv.org/ftp/arxiv/papers/2003/2003.09982.pdf
[2] Ipatov S.I., Migration of bodies to the Earth and the Moon from different distances from the Sun // The Ninth Moscow Solar System Symposium 9M-S3, 2018, https://ms2018.cosmos.ru/, 9MS3-SB-11, p. 104-106, https://elibrary.ru/item.asp?id=37178225
[3] Ipatov S.I. Migration of planetesimals to the Earth and the Moon from different distances from the Sun // 50th LPSC, 2019, #2594. https://www.hou.usra.edu/meetings/lpsc2019/pdf/2594.pdf . e-poster: https://www.hou.usra.edu/meetings/lpsc2019/eposter/2594.pdf
[4] Levison H.F., Duncan M.J. The long-term dynamical behavior of short-period comets // Icarus, 1994, 108, 18-36.
[5] Ipatov S.I., Mather J.C. Migration of Jupiter-family comets and resonant asteroids to near-Earth space // Annals of the New York Academy of Sciences, 2004, 1017, 46-65. http://arXiv.org/format/astro-ph/0308448
[6] Ipatov S.I., Mather J.C. Comet and asteroid hazard to the terrestrial planets // Advances in Space Research, 2004, 33, 1524-1533. http://arXiv.org/format/astro-ph/0212177.
[7] Ipatov S.I., Probabilities of collisions of planetesimals from different regions of the feeding zone of the terrestrial planets with the forming planets and the Moon // Solar System Research, 2019, 53, 332-361. http://arxiv.org/abs/2003.11301
How to cite: Ipatov, S.: Migration of planetesimals from beyond Mars’ orbit to the Earth, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-71, https://doi.org/10.5194/epsc2020-71, 2020.
It is believed that many near-Earth asteroids are rubble piles: aggregates of smaller regolith particles bound together by self gravity and cohesive forces, formed from the reaccumulation of much larger, monolithic progenitors after catastrophic collisions [1]. The recent OSIRIS-REx and Hayabusa2 sample-return missions to Bennu and Ryugu, respectively [2, 3], have shown complex and diverse regolith surfaces on rubble piles, with grains spanning from millimeters to tens of meters in radius, evidence of granular flow (slumping), and artifacts such as large surface boulders without surrounding craters (potentially indicating vertical regolith migration).
A successful approach to simulating rubble piles is the discrete element method (DEM), which uses individual (typically spherical) particles to represent the constituent blocks of the rubble pile, with particle properties (including friction parameters) chosen to mimic bulk properties of real materials, such as angle of repose. Particles that make up real granular materials, however, are most often not spherical. The shapes of real grains make it more difficult for them to slide past one another, can create quasi-stable equilibria when grains are vertically stacked, and cause the material to “bulk” (creating more void space and less efficient packing). These phenomena of real granular materials are not well exhibited by spherical particles, thus the most accurate way to capture a realistic picture of granular dynamics is to use irregularly shaped particles instead of spheres in simulations. The aim of this work is to present a new algorithm for handling simulations using large numbers of irregularly shaped particles with pkdgrav, a DEM code that has been used effectively in the past to model granular dynamics on rubble piles [4, 5, 6, 7], and show that simulating with irregularly shaped grains can lead to results more akin to real granular systems.
We construct irregular particles by “gluing” spheres together to make bonded (rigid) aggregates. Originally, aggregate routines for pkdgrav were written to handle a few large aggregates made up of many individual particles. In this scheme, aggregate properties are tracked in serial, where a brute force search finds particles belonging to an aggregate then operates on them, searching through every particle on every processor for every aggregate in the simulation. An inefficiency arises when the number of aggregates is similar to the total number of particles (N), as in a simulation of a granular bed made up of small aggregates, each only containing a few particles. Here, the brute force search becomes an ∼O(N2) operation. This is prohibitively expensive for processes requiring large N, like granular dynamics simulations.
We solved the issue of efficiently locating particles that belong to an aggregate by forcing a reordering of the particles before the search ever occurs, to put them in order of their aggregate index numbers on each processor. We then exploit this particle ordering by replacing the original brute-force search with a binary-search algorithm [8] that scales as O(NlogN) and added a “cache-line” method. The binary search is used whenever the particle information is not immediately known, i.e., not in the cache (like the first time a search needs to occur in a simulation). The cache line stores the index of the previously found particle in order to easily step forward and find the next particle that needs to be acted on when the code returns to the function—this is a linear operation in N (O(N) scaling), so it scales well. Preliminary tests show a 25–50% decrease in total (wallclock) runtime for moderate resolution simulations using this algorithm overthe original scheme, and expect better performance at higher resolutions.
To show the importance of being able to simulate irregularly shaped granular material, we apply our method to an investigation of a scientific application for granular dynamics in low gravity: the Brazil-nut effect. The Brazil-nut effect (BNE) [5, 6, 9] is a mechanism for the vertical migration of boulders in a granular medium that has been suggested as an explanation for exposed boulders on asteroid surfaces. In granular dynamics, the BNE is a method in which frictional interactions between particles in a granular medium cause larger blocks to rise to the surface when the medium is subjected to repeated seismic shaking (like Brazil nuts rising to the top of a shaken jar of mixed nuts).
In previous studies with spherical particles, it was shown that increased interparticle friction accounted for a more efficient rise of the large subsurface intruder, but in our preliminary simulations, when simulating with irregular grains, we show that interparticle friction makes the void-filling mechanism less efficient and thus the Brazil nut rises slower. We will explore a broad parameter space in particle size ratio, grain shape, interparticle friction, and interparticle cohesion, to establish how more realistic, irregularly shaped particles exhibit the BNE in low-gravity environments.
How to cite: DeMartini, J. and Richardson, D.: An Efficient Algorithm for Operating on Large Numbers of Aggregate Particles with Applications to Simulating the Dynamics of Irregularly Shaped Grains, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-383, https://doi.org/10.5194/epsc2020-383, 2020.
In 2019, the New Horizons spacecraft flew by the Kuiper belt object (486958) Arrokoth, a member of the cold classical population in the Kuiper belt. Images returned from the New Horizons flyby reveal that Arrokoth is a contact binary composed of two distinct lobes joined by a narrow contact region (the "neck"). The lobes are roughly similar to oblate spheroids in shape and the long axis of the whole body is about 35 km long [1]. Cold classical Kuiper belt objects like Arrokoth are thought be among the most primitive bodies in our solar system, forming in their current positions from the solar nebula over 4 Gyr ago and remaining nearly undisturbed since. The mechanism by which Arrokoth formed is thus of great interest and may lend unique insight into the formation of terrestrial bodies in the outer solar system. Under the assumption that Arrokoth is the union of two distinct progenitor bodies, we use a numerical code to model the final stage of the merger that created this unique object. We investigate a range of possible merger parameters and use the results to determine the most plausible scenarios. We describe the methods we used to simulate the merger and detail our results. The work presented here is described in greater detail in Marohnic et al. 2020, in press for the Icarus special issue on Kuiper belt science [2].
We use the parallel N-body code 'pkdgrav' to model the Arrokoth merger [3]. pkdgrav uses the soft-sphere discrete element method (SSDEM) to compute collisions between spherical particles. SSDEM resolves contacts by allowing particles in contact to interpenetrate slightly as a proxy for deformation. Restoring forces are modeled as damped springs and static, rolling, and twisting friction are accounted for as well. Both lobes are modeled separately, as "rubble piles" composed of spherical particles. In total, each simulated merger event uses between 100,000 and 200,000 particles. Our simulations test the effects of varying impact angle and speed, material cohesion strength, body shape, bulk density, and spin (see Figure 1).

Figure 1: A gentle contact between two rubble-pile bodies formerly in a close, synchronous orbit. The shape of the progenitor bodies are preserved, and the neck-like contact area remains narrow and well-defined.
The results of our suite of simulations suggest that any merger that could produce an object like Arrokoth would have to have been quite slow (roughly equal to the mutual escape speed of the progenitor objects or slower) and at a near-grazing angle. We find that the most plausible scenario is a gradual inspiral of two bodies in a close synchronous orbit leading to final, gentle merger.
Acknowledgements: The simulations described here were performed on the Deepthought 2 cluster at the University of Maryland, College Park. This work was supported by NASA grant NNX15AH90G awarded by the Solar System Workings program, by a University of Maryland Graduate School Research and Scholarship Award, and by NASA's New Horizons project via contracts NASW-02008 and NAS5-97271/TaskOrder30.
[1]: Stern, S.A., Weaver, H.A., Spencer, J.R., Olkin, C.B., Gladstone, G.R., Grundy, W.M., Moore, J.M., Cruikshank, D.P., Elliott, H.A., McKinnon, W.B. and Parker, J.W., 2019. Initial results from the New Horizons exploration of 2014 MU69, a small Kuiper Belt object. Science, 364(6441).
[2]: Marohnic, J.C., Richardson, D.C., McKinnon, W.B., Agrusa, H.F., DeMartini, J.V., Cheng, A.F., Stern, S.A., Olkin, C.B., Weaver, H.A. and Spencer, J.R., 2020. Constraining the final merger of contact binary (486958) Arrokoth with soft-sphere discrete element simulations. Icarus, p.113824.
[3]: Stadel, J.G., 2001. Cosmological N-body simulations and their analysis (Doctoral dissertation, University of Washington).
How to cite: Marohnic, J. C., Richardson, D. C., McKinnon, W. B., Agrusa, H. F., DeMartini, J. V., Cheng, A. F., Stern, S. A., Olkin, C. B., Weaver, H. A., and Spencer, J. R.: Constraining the final merger of contact binary (486958) Arrokoth with soft-sphere discrete element simulations, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-378, https://doi.org/10.5194/epsc2020-378, 2020.
The availability of large data set of asteroids proper elements made
possible in recent years a deeper and deeper analysis of the structure
of the asteroid dynamical families in the Main Belt (Milani et al.,
2014). At the same time the Yarkovsky effect, the importance of which
has been largely recognized, has imposed a new data interpretation
paradigm. Precisely the Yarkovsky effect is the basis of one
estimation method of the age of the asteroid families analyzing the
shape of the family members distribution in the plane diameter versus
proper semimajor axes, the so called V-shape (Spoto et al., 2015).
This very important goal has been achieved under the assumption that
the post-formation evolution of the semimajor axes producing the
V-shape structure was linear in time and dominates their present
dispersion. In particular the impact of the initial values of the
fragments ejection velocities, determining the initial dispersion of
the semimajor axes, is supposed to be marginal, assumption probably
correct for old enough families. If this is not the case, the initial
ejection velocity field introduces a more or less large bias in the
age determination. We conducted a series of numerical experiments
simulating the formation and dynamical evolution of the asteroid
families in order to evaluate the extent of this bias.
Moreover in our model we included a series of mechanisms concerning
the initial break-up outcomes. In particular two aspects have been
taken into account: the effect of the initial gravitational
re-accumulation on the structure of the V-shape and the effect of
possible correlations between spin direction and ejection velocity
direction (Milani et al., 2019). We show how the former effect could
be responsible of some systematic features of the V-shape structure,
while the second can in some cases mitigate the bias in the age
determination introduced by the initial ejection field.
Finally we discuss the role of the family members spin axes evolution
due to non destructive collisions, affecting the efficiency of the
Yarkovsky-driven semimajor axis mobility. We show how this latter
mechanism modifies the determination of the age.
References:
Milani A., Cellino A., Knezevic Z., Novakovic B., Spoto F., Paolicchi P.
2014.
Asteroid families classification: Exploiting very large datasets.
Icarus, 239, 46-73.
Spoto F., Milani A., Knezevic Z.
2015.
Asteroid family ages.
Icarus, 257, 275-289.
Milani A., Knezevic Z., Spoto F., Paolicchi P.
2019.
Asteroid cratering families: recognition and collisional interpretation.
Astronomy and Astrophysics, 622, A47.
How to cite: Dell'Oro, A., Boccenti, J., Spoto, F., Paolicchi, P., and Knezevic, Z.: Asteroid families age determination: the role of the physical effects, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-90, https://doi.org/10.5194/epsc2020-90, 2020.
Asteroid families are groups of asteroids that are the product of collisions or of the rotational fission of a parent object. These groups are mainly identified in proper elements or frequencies domains. Because of robotic telescope surveys, the number of known asteroids has increased from about 10,000 in the early 90's to more than 750,000 nowadays. Traditional approaches for identifying new members of asteroid families, like the hierarchical clustering method (HCM), may struggle to keep up with the growing rate of new discoveries. Here we used machine learning classification algorithms to identify new family members based on the orbital distribution in proper (a,e,sin(i)) of previously known family constituents. We compared the outcome of nine classification algorithms from stand alone and ensemble approaches. The Extremely Randomized Trees (ExtraTree) method had the highest precision, enabling to retrieve up to 97% of family members identified with standard HCM.
How to cite: Carruba, V.: Machine learning classification of new asteroid families members, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-36, https://doi.org/10.5194/epsc2020-36, 2020.
Since December 2013, the GAIA spacecraft (ESA) is observing the sky with an unprecedented accuracy. Gaia DR2, released in April 2018, contains the position and epoch of 14099 known solar system objects (SSOs) representing more than 2 million observations collected during the first 22 months of operation. In this presentation, we used the new released INPOP19a planetary ephemerides to perform their orbital adjustment and compare them to radar and optical ground-based observations. In order to reduce the time of computation and in anticipation of the huge amount of datas expected with future DR3, a specific solving strategy for the normal equations of the Gauss-Newton algorithm is presented, making the best use of the model design. We obtain post-fit residuals that are closed to the expected performance of GAIA and overall consistent with the values announced by the DR2 reference orbit determination (see Gaia Collaboration et al 2018). In order to disccus the reliability of the obtained orbits, a combination with radar and optical ground based observations was performed for 23 objects using two different numerical methods: a systematic exploration of the weighting scheme coupled with a residual post-fit analysis, and a Least Square Variance Component Estimation adjustment algorithm (LSVCE). Such methods can be extended to all inverse problems within the framework of least-square formalism.
How to cite: Deram, P., Fienga, A., and Gastineau, M.: Asteroids orbit determination using INPOP19a adjusted on GAIA observations: strategy and validation. , Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-238, https://doi.org/10.5194/epsc2020-238, 2020.
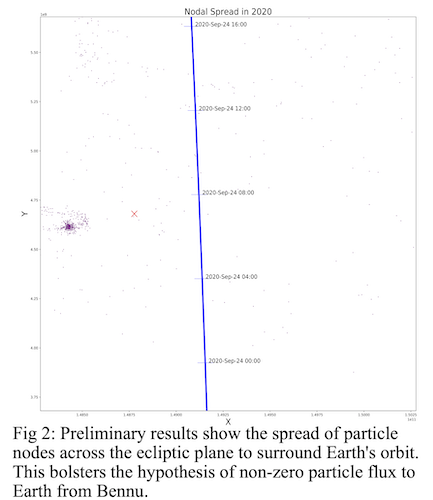
NASA’s OSIRIS-REx mission set out in September of 2016 to survey and sample the near-Earth asteroid (101955) Bennu. During observations of Bennu, mission scientists observed centimeter-scale pebbles ejecting off the surface of the asteroid [1]. Many of these particles have been observed to follow hyperbolic trajectories, and the intersection of the orbits of Bennu and Earth suggests the possibility of particle flux at Earth [2]. We simulate the evolution of the motion of particles ejected from Bennu with a focus on potential meteor activity at Earth.
We developed a complex simulated environment that accounts for the most potent perturbing gravitational bodies and solar radiation forces that are applicable to our centimeter-scale size range [3]. We use REBOUND, an orbital integration API developed by Hanno, Rien and Tamayo [4], augmented with REBOUNDx, developed by Tamayo et al. [5], to include solar radiation pressure and Poynting-Robertson (PR) drag. Bennu is modeled as a massless object, though great care is spent ensuring Bennu’s orbital accuracy as the particles are integrated towards well-defined close approaches in the near future [6]. Contrary to most meteoroid stream evolution studies, our simulations release particles from Bennu at a regular cadence (600 grams per week) throughout its orbit to resemble mission observations.
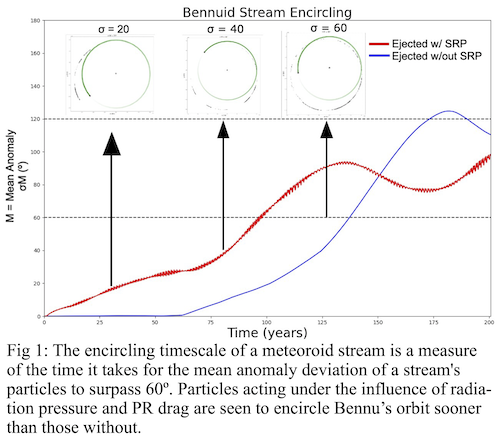
To test the accuracy of the model and integrator, we prepared test cases for expected behavior. Recreating examples of particle resonance traps due to PR drag confirmed the implementation of the non-gravitational forces. Observations of the particle stream circularization (Fig. 1) and associability over time were also indicative of expected behavior. Additionally, planetary bodies were initialized from a JPL ephemeris (DE 431) and continuously compared to these values as a reference. The modeled solar system maintained an accuracy of 10-1 to 101 arcseconds of mean anomaly for their expected positions, giving us confidence in our methods.
Towards the main objective of observing Earth-particle interactions, limitations in processing power and time encourage us to run simulations at particle production rates lower than the mass loss observed at Bennu by a factor of 100. Earth-particle close approaches are recorded annually during simulations. These data are later converted into stream density estimates and Earth impact probabilities through analysis on the B-plane [7]. This formalism enables the calculation of the statistical likelihood of impact with Earth for all of the particles produced in the simulation over the 348 years of interest (1788–2135); the years over which Bennu’s position is best constrained [6]. Such results now inform our conclusions on zenith hourly rate flux measurements at Earth.
This work will be of practical importance for professional and amateur astronomers searching for Bennuid meteors. While the exact particle production mechanisms are still open to debate, we are hopeful that this initial work can be generalized to encompass the entire near-Earth asteroid population. This work, together with additional particle ejection observations and analyses from the OSIRIS-REx mission, will pave the way to a full understanding of this astronomical phenomenon.
References:
[1] D.S. Lauretta and C.W. Hergenrother et al. (2019). Science 366, 1217-1227.
[2] Q. Ye (2019) Notes of the AAS 3, 56.
[3] P. Jenniskens et al. (2011) Icarus 216, 40-61, & cams.seti.org
[4] H. Rien and S.F. Liu (2012) Astronomy & Astrophysics 537, A128.
[5] Tamayo, Daniel, et al. (2020) Monthly Notices of the Royal Astronomical Society 491.2
[6] S.R. Chesley et al. (2014) Icarus 235, 5-22
[7] D. Farnocchia et al. (2019) Springer, Celestial Mechanics and Dynamical Astronomy.
How to cite: Melikyan, R., Clark, B., Hergenrother, C., Chesley, S., Nolan, M., Ye, Q., and Lauretta, D.: A Natural Sample Delivery Mechanism: Estimating the Flux of Bennuid Meteors, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-428, https://doi.org/10.5194/epsc2020-428, 2020.
Introduction
On September 30, 2022, NASA’s Double Asteroid Redirection Test (DART, [1]) mission will be the first space mission demonstrating the kinetic impactor method for planetary defense. DART will impact Didymos B (a 164±18 m secondary of asteroid (65803) Didymos [2]) with its mass of 650 kg and at a speed of 6.6 km/s. Such impact is expected to change the secondary orbital period by about 10 minutes. DART will carry as a piggyback the Light Italian Cubesat for Imaging of Asteroids (LICIACube, [3]) which will be released from DART ten days before the impact. LICIACube will provide evidence of the impact and will take multiple images of the target up to a distance of ~55 km from the target. The LICIACube narrow and wide angle cameras - LEIA (LICIACube Explorer Imaging for Asteroid) and LUKE (LICIACube Unit Key Explorer), respectively – will capture the post-impact processes coming from in situ events, such as the newly formed crater, the expanding ejecta and the dynamics of its plume. In particular, the measurement of the motion of the slow (<5 m/s) ejecta in the plume will be feasible with LICIACube, thus allowing description of its structure and the evolution of the dust size and velocity distribution. In this work, we study the motion of the plume evolution in terms of dust numerical simulations. To accomplish this, we modified the non-spherical dust model [4] and applied it to an asteroid impact scenario using analytical expressions to estimate the initial velocity and mass of ejecta. As input we used the ejecta impact properties (ejecta mass, velocity, launch position distribution, orientation) constrained with iSALE numerical simulations [5]. We discuss the influence of the non-sphericity of the particles on the dynamical properties of the plume, such as the velocity and dust spatial distribution, and address the optical thickness not only in terms of particle size distribution but also as a function of particle shape and orientation.
Dust plume model
We use a 3D+t non-spherical dust model that solves the Euler dynamical and kinetic equations. Considering free-collisional dust regime we study the effects on the particle dynamics provided with different shapes, initial particle orientation and velocities as well as torque. Torque is computed from the law of variation of the angular momentum by using the Euler dynamic equations. The particles are assumed to be homogeneous, isothermal convex bodies, having the same physical properties of the target. The dust motion is governed by solar radiation pressure force, initial dynamical parameters (speed, orientation and torque) and gravity of the asteroid binary system. To compute the gravity we take into account that Didymos B is orbiting at distance of ~1.18 km the Didymos primary (780±80 m in size) [6].
As input we use the physical parameters obtained via numerically simulated impact into low-gravity and strength- dominated asteroid surface done with the iSALE numerical code [5]. A detailed description of the parameters set used in the impact modelling are reported in Table 1. As an example, in Fig.1, we show the iSALE simulation of the spatial distribution of tracer particles for 50 ms after the impact.
Table 1: Paremeters used for iSAle simulation. A detailed description can be found in [5].
Fig. 1: A snapshot of the formation of the crater resulting from the iSALE modelling performed with parameters reported in Table 1. The colorbar represent the peak pressure of the ejecta tracer particles.
Non-spherical dust motion in the plume
We have studied the motion of non-spherical particles after the impact assuming various set of initial parameters coming from the iSALE simulations, such as particle mass, shape, initial orientation, launch position and computed velocity. The Didymos system physical parameters and particle temperature were taken from [7]. Here, in Fig. 2, we show the velocity and the distance from the surface where it has been reached for a prolate spheroid (aspect ratio = 2 [4]) with assumed density 2600 kg/m3. The particle mass is 7.45 x10-2 kg, the initial velocity 0.94 m/s, the launch position is 11 m from the center of the crater and the initial tilt of the initial velocity vector away from local surface normal is 46 degrees. We plotted the results for two cases: 1) only the Didymos B gravity field is considered and 2) the gravity of the whole binary is used. Our results show that the particle dynamics is sensitive to parameters such as orientation and ejection velocity.
Fig. 2: Velocity and distance at which it has been achieved for a prolate particle (aspect ratio a/b = 2). The complete set of parameters is given in the text. The solid line indicates the case when only gravity of Didymos B was considered and the dashed line when the gravity of the whole binary was used (binary was approximated as a mass point).
This study of dust dynamics in expanding ejecta together with LICIACube plume evolution images can further constrain the momentum transfer efficiency estimation as well as the ejecta velocity and dust size distribution in the “far-field” expanding plume.
Acknowledgments
This research was supported by the Italian Space Agency (ASI) within the LICIACube project (ASI-INAF agreement AC n. 2019-31-HH.0).
References
[1] Cheng A. F. et al. (2016) Planet. Space Sci., 121, 27-35. [2] de León, J. et al. (2010) Astron. Astrophys, 517, A23. [3] Dotto, E. et al., (submitted), Planet. Space Sci. [4] Ivanovski S. et al. (2017), Icarus 282, p. 333 - 350. [5] Raducan, S. D. et al. (2019), Icarus, 329, p. 282 - 295. [6] Michel, P. et al. (2016) Adv. Space Sci. 57, p. 2529 - 2547. [7] Yu Y. et al. (2017), Icarus 282, p.313 - 325
How to cite: Ivanovski, S. L., Lucchetti, A., Pajola, M., Bertini, I., Zanotti, G., Perna, D., Dotto, E., Della Corte, V., Amoroso, M., Pirrotta, S., Capannolo, A., Lavagna, M., Rossi, A., Fahnestock, E. G., Hirabayashi, M., Raducan, S. D., Meneghin, A., Poggiali, G., Brucato, J. R., and Cremonese, G. and the and the LICIACube team: Modelling dust distribution in the ejecta plume from nonspherical dust dynamics perspectives in support of the LICIACube and DART missions, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-1096, https://doi.org/10.5194/epsc2020-1096, 2020.
In the Solar System, several different types of small bodies can be found, whose histories can deviate highly from each other, including time and process of formation, followed by collisional or other evolutionary processes. For cometary nuclei, the history and formation remain unsolved and different hypotheses exist, which may explain their past (Weissman et al. 2020). In this study here, the focus lies on the thermophysical properties of small bodies. Different formation scenarios lead to different properties of the resulting bodies. In the scenario of the gravoturbulent collapse of a pebble cloud, macroscopic void spaces remain in the body (e.g. Blum et al. 2014, 2017). In contrast, the hierarchical accretion leads to more compact bodies without large voids (e.g. Davidsson et al. 2016). This effects the thermophysical behaviour, as in the first case, besides the network conductivity of the solid material, also radiation can efficiently transport heat through the voids. The radiative heat conductivity can be described as follows:
λrad = 16/3 σ T3 Λ(Φ)
where σ, T, Λ and Φ are the Stefan-Boltzmann constant, the temperature, the radiative mean free path and the volume filling factor, respectively. The network part of the heat conductivity can be written as
λnet = H λagg/par(T)
with the Hertz factor H and the aggregate or particle thermal conductivity λagg/par (see Gundlach and Blum 2012, and Gundlach et al 2020 for details). The radiative thermal conductivity has a much higher dependency on temperature than the network part.
Here, we address the question, how radiation influences the thermal behaviour of a planetesimal in a measurable way. Therefore, the following steps are foreseen: a thermophysical model is set up, which calculates the heat transport in a small body that is illuminated by the Sun. For simplicity, we assume a circular orbit around the Sun at several heliocentric distances without obliquity and varying rotational periods. The model solves the heat transport equation in a one-dimensional approximation. In this study, we focus on the surface temperature as the output. This is motivated by the measurement capabilities of most spacecraft visiting small bodies. To measure the surface temperature is relatively easy, often done and enough accurate compared to the remote measurements of inner temperatures.
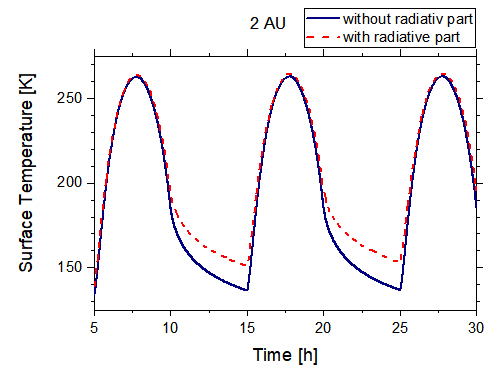
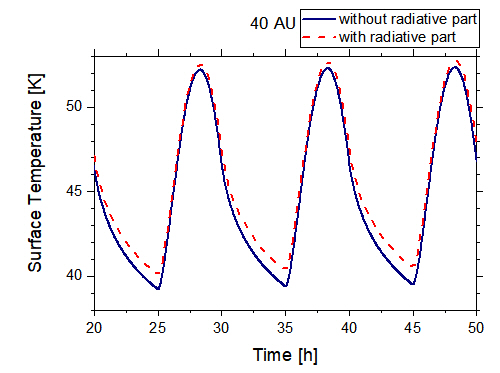
Figure 1 : Results of the thermophysical modelling for 2 AU (left) and 40 AU (right): surface temperature over time for the simulation with (dashed) and without (continuous) radiative part.
With the described model, the influence of the radiative part of the thermal conductivity is studied by varying it in different setups, namely heliocentric distance, and rotation period. Thereby, the Fourier number, which represents the numerical accuracy of the model run, is optimized to be near its favourable value of 0.5. In a first attempt, only the surface temperature of the equator was regarded. An exemplary plot of two model runs is shown in Figure 1 for a rotation period of 10 hours and at heliocentric distances of 2 AU and 40 AU, respectively. For each heliocentric distance, the maximal temperature is similar for the two cases (with and without radiative conductivity) studied, but during the night, cooling behaves differently. In the case of 2 AU, a median thermal conductivity of 0.02 W/(m K) was calculated; for 40 AU, the median thermal conductivity reduces to 0.003 W/(m K). In this colder regime, the differences at night are reduced. In a next step, this analysis will be expanded to the surface temperature of the meridian from pole to equator, assuming a spherical body.
The first results indicate that for some parameter sets, the two scenarios show sufficient differences to be distinguishable by measurement. Comparing the results of our study to measured data from small bodies could allow further insights into the formation or evolutionary paths of small bodies. More detailed results and conclusions will be presented at the EPSC 2020.
Acknowledgement:
This work was funded through the DFG project BL 298/27-1.
References:
Blum J., Gundlach B., Mühle S., Trigo-Rodriguez J. M., 2014, Icarus, 235, 156
Blum J. et al., 2017, MNRAS, 459, S755
Davidsson B. J. R. et al., 2016, A&A, 592, A63
Gundlach B., Blum J., 2012, Icarus, 219, 618
Weissman P., Morbidelli A., Davidsson B., Blum J., 2019, Space Sci. Rev., 216, 6
How to cite: Bischoff, D., Gundlach, B., and Blum, J.: Thermophysical modelling of small bodies: influence of the radiative thermal conductivity, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-951, https://doi.org/10.5194/epsc2020-951, 2020.
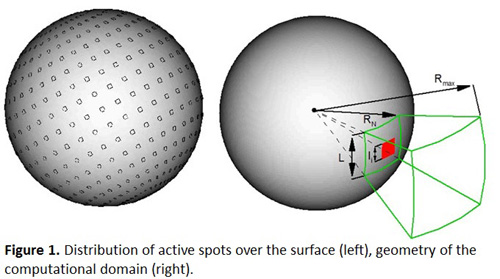
In the present work we study the case when gas production Q of the nucleus is formed by the gas emission from a set of closely located (with interval L) spots (see Fig.1) with sizes li much smaller than the radius of the nucleus Rn. We study the structure of the flow in the mixing region for different combinations of li, L, Q and define parameters of the resulting uniform flow. Due to a large number of spots (i.e. L<<Rn) and taking into account the symmetry, it is possible with sufficient precision to restrict the computational domain as shown in Fig.1 (the boundaries of the domain are shown in green, the active spot is shown in red). Note that the Fig.1 is made not to scale.
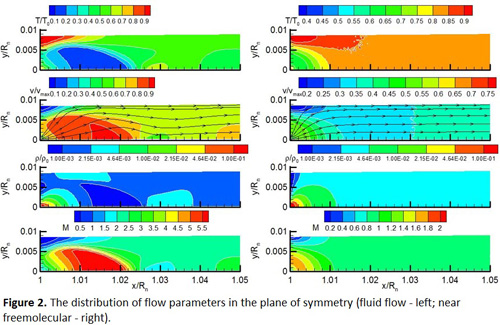
For the same geometry (i.e. Rn, li, L) but different production rate Q the flow structure in the mixing region can be radically different. For example, Fig.2 shows the distributions of temperature, velocity, density and Mach number (from top to bottom) in the plane of symmetry.The flow close to fluid contains multiple shock structures leading to the non-monotonous and periodic variation of flow parameters (see Fig.2 left). In a rarefied flow the flow structures are diffused and the flow faster become uniform (see Fig.2 right). The flow from inhomogeneous surface can be conventionally divided into two regions: (1) a mixing region; and (2) a uniform flow. The flow in the mixing region is multidimensional i.e. with variation of parameters not only along the radial direction. The uniform flow is a result of viscous dissipation of the flow in the mixing region and it is one dimensional with variation of parameters along radial direction only (as it would be in the case of expansion from a homogeneous sphere).
An important feature of the flow from inhomogeneous surface (with respect to the flow from homogeneous surface) is the occurrence of a non-zero lateral flow velocity in the vicinity to the surface. In all cases under consideration the lateral velocity reached magnitudes comparable with the radial flow velocity. This can have a very strong impact on the acceleration of the dust especially on the initial direction of acceleration.
Conclusions:
- The results of our study show that in the case of inhomogeneous emission from the surface the uniform flow may be formed at the altitudes comparable with Rn. Therefore, substitution by a uniform flow should be done above this altitude.
- The flows from inhomogeneous and homogeneous spheres with the same surface temperature and total gas production rates are not equivalent (i.e. parameters of the resulting uniform flow are not the same as parameters in the flow from homogeneous surface at the same distance) due to difference in stagnation energy. This non-equivalence becomes more pronounced with decrease of flow rarefaction (increase of gas production Q).
- For the correct substitution of the flow from inhomogeneous surface on the uniform flow we propose to use parameters on the sonic surface (and we provide position of this surface and distribution of parameters on it for a broad range of conditions).
- In the mixing region, the gas emanated from active spots expands more intensively then from uniform surface. And furthermore, the inhomogeneity may cause strong lateral flow in the vicinity to the surface. This may have an important impact on the initial acceleration of dust.
Acknowledgements:
This research was also supported by the Italian Space Agency (ASI) within the ''Partecipazione italiana alla fase 0 della missione ESA Comet Interceptor'' (ASIINAF agreement n.Accordo Attuativo" numero 2020-4-HH.0 ).
How to cite: Zakharov, V., Bykov, N., Rodionov, A., Ivanovski, S., Della Corte, V., Rotundi, A., Fulle, M., and Marschall, R.: Mixing region over a surface of cometary nucleus with small-scale inhomogeneities, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-219, https://doi.org/10.5194/epsc2020-219, 2020.
There is a basic understanding of the way gases are released from cometary nuclei in order to form the gas and dust comae as they approach the Sun. We know that the production of these gases is driven by the incident solar radiation on the nucleus, and this leads to the sublimation of cometary ices. The composition of the coma depends on the composition and thermal properties of its nucleus. In general, comets are often assumed to be a mixture of ice and dust [1, 2, 3]. There is however a lack of knowledge on the actual internal structure of comets both at macroscopic and microscopic levels. For comet 67P/Churyumov-Gerasimenko (67P/CG), for example, the Rosetta Orbiter Spectrometer for Ion and Neutral Analysis (ROSINA) determined H2O, CO2, CO and O2 to be the most abundant gases in the coma[4, 5, 6], which is a clear indication of the composition of dominant ices within the nucleus. How these different ices are physically related to each other and distributed within the nucleus is a more intricate issue for which we have no clear answer at this time.
Previous studies have produced mathematical models of the surface layer of cometary nuclei based on heat and gas diffusion through pores [7, 8, 9, 10, 11]. These studies use a one-dimensional geometry. Our aim is to use a similar approach to model the gas activity distribution around three-dimensional nuclei. This is known in the literature as "standard thermal model" for slow-rotators [12, 13, 14] and it calculates the insolation condition at a certain heliocentric distance for one point on the surface after Nrot nucleus rotations on its axis. Here in the influence of thermal inertia combined with sub-surface sublimation sources at different depths and the resulting gas flow field is investigated using both H2O and CO2 as driving volatiles. The additional complexity in geometry prevents more sophisticated numerical solutions. We have therefore ignored the influence of heating of gas through collision with a hotter dust mantle in the present model, considering that these additional effects probably only result in relatively small changes in the position of the sublimation front due to the exponential change in sublimation rate with temperature.
We apply this study to a spherical nucleus comet, but we adopt some of the rotational and surface properties of the target of the Rosetta mission, comet 67P/CG. In order to model gas activity in the inner coma, we have chosen a nucleus with a 2 km radius and an outer limit of our simulation domain to be at 8km from the surface of the comet. The 3D Direct Simulation Monte Carlo method is then used to model the coma as a sublimation-driven flow.
Simulation results displayed in figure 1 show that thermal inertia and the depth of the sublimation front can have a strong effect on the emission distribution of the flow at the surface. We determine that for cases with a thermal inertia larger than zero, the H2O distribution can be shifted in rotation by about 20º relative to models with no thermal lag. For CO2 cases with different thermal inertia values and sublimation fronts, the activity distribution can be shifted towards the terminator making CO2-ice the main source of nightside activity. This would be consistent with observations of gas density and dust column density above the nightside hemisphere of the nucleus of 67P/CG.
There is also a strong effect of CO2 activity on the distribution of the H2O flow field in the nightside of the comet, which can decrease the amount of H2O by up to 98% compared to a pure H2O case. CO2 gas also decreases the temperature of the flow, as well as the flow velocities on the nightside. In the cases we studied, temperatures were reduced by a factor of 2 and velocities were up to 150m/s slower than the cases without CO2 activity.
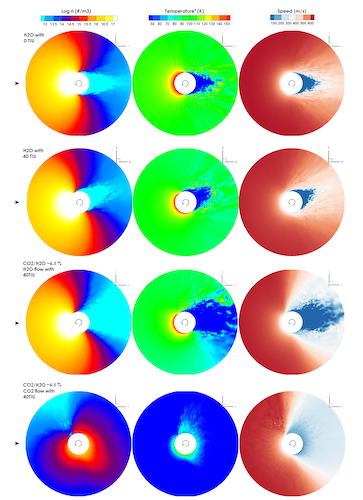
Figure 1: Slice of the 3D simulation domain on the xy-plane, with information of number density, temperature and velocity within the flow for a case without thermal inertia (upper row), a pure H2O case with thermal inertia of 40 J/(m2K√s) (second row) and a mixture case with 40 J/(m2K√s) (third and fourth row). The arrows on the left side indicate the position of the sub-solar point.
Acknowledgements
This work has been carried out within the frame- work of the National Centre of Competence in Re- search PlanetS supported by the Swiss National Sci- ence Foundation. The authors acknowledge the finan- cial support of the SNSF.
Raphael Marschall acknowledges the support from the Swiss National Science Foundation grant 184482.
References
[1] F. L. Whipple: A comet model. I. The acceleration of comet Encke, Astrophysical Journal, Vol. 111, p375-394, 1950.
[2] D. A. Mendis and G. D. Brin, 1977, The Moon, 17, Issue 4, p. 359-372.
[3] F. P. Fanale and J. R. Salvail, 1984, Icarus, 60, Issue 3, p. 476-511.
[4] M. Hässig et al., 2015, Science, 347, Issue 6220.
[5] L. Le Roy et al., 2015, A&A, 583, A1.
[6] A. Bieler et al., 2015, Nature, 526, p. 678-681.
[7] Y. V. Skorov and H. Rickman, 1995, Planetary and Space Science, 43, Issue 12.
[8] Y. V. Skorov et al., 1999, Icarus, 140, Issue 1.
[9] Y. V. Skorov et al., 2001, Icarus, 153, Issue 1.
[10] Y. V. Skorov et al., 2002, Earth Moon and Planets, 90.
[11] B. Davidsson and Y. Skorov, 2004, Icarus, 168, Issue 1, p. 163- 185.
[12] L. Lebofsky and J. Spencer ,1989, Asteroids II: Radiometry and thermal modeling of asteroids.
[13] M. Festou, H. U. Keller and H. A. Weaver, 2004, Comets II, University of Arizona Press.
[14] W.F., Huebner et al., 2006, Heat and Gas Diffusion in Comet Nuclei, The International Space Science Institute.
How to cite: Pinzón Rodríguez, O. J., Marschall, R., Gerig, S.-B., Herny, C., Wu, J.-S., and Thomas, N.: The effect of thermal inertia on the outgassing and gas dynamics in the inner-coma of cometary nuclei, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-417, https://doi.org/10.5194/epsc2020-417, 2020.
OSIRIS (Optical, Spectroscopic, and Infrared Remote Imaging System, [1]) was the scientific camera system on board the Rosetta spacecraft and acquired a huge image dataset of the nucleus and the inner dust coma of comet 67P/Churyumov-Gerasimenko (hereafter 67P). The 2D-projections of the 3D dust coma contain information about the surface source distribution and physical processes governing the dust outflow in the innermost tens of kilometres above the nucleus surface. Numerical simulation has become an important tool in the attempt to disentangle and study these different processes at work. Here, we study the dust outflow behaviour with the help of “azimuthal average” [2, 3] profiles in Rosetta/OSIRIS data and artificial simulation images. Further, we look at the dayside-to-nightside brightness ratio (DS:NS) to characterise the relative difference in brightness from the dayside to the nightside coma [4]. A low DS:NS ratio indicates that the nightside coma is not much brighter than the dayside coma. This is not expected for a coma where outgassing is only originating from directly illuminated surface areas (as we show in our simulation results), but it is observed in OSIRIS images of the coma of 67P.
We show in our simulation results that direct activity from the non-illuminated nightside of 67P is needed to explain the low ratio of brightness from the dayside to the nightside coma observed in OSIRIS images. The DS:NS ratio in a series of 4 images acquired at 90° phase angle during one comet rotation on 11. April 2015 was determined to be 2.49 ± 0.18 on average. In our simulation results, such low DS:NS values can only be reached if the non-illuminated areas on the nucleus are outgassing in addition to the illuminated dayside regions. With only the directly illuminated surface outgassing the dayside-to-nightside asymmetry is factors of 4-10 too high. With additional outgassing from the nightside on the level of ~10% of the total gas production rate, the correct level for dayside-to-nightside brightness can be reproduced in artificial simulation images. Furthermore, the dust outflow behaviour in our simulation results matches the observed dust outflow behaviour better if nightside activity is present in the model. We additionally show that the DS:NS ratio increases when the comet moves towards perihelion (Fig. 1). We suggest that outgassing CO2 or CO rather than water is driving the direct activity from the nightside [5] and that the increasing DS:NS ratio towards perihelion is a sign of the increasing domination of H2O outgassing over outgassing of the more volatile gas species.
Figure 1: DS:NS ratio values as a function of days to perihelion.
For our simulations we use a two-step approach to simulate the 3D dust coma in the innermost 10 km around the nucleus of 67P. In a first step, the 3D gas field is calculated using a Direct Simulation Monte Carlo (DSMC) approach. In this study we use water as the only gas species in our simulations. Nightside activity is artificially introduced by letting the non-illuminated surface facets be active, so that their cumulative gas production rate is ~10% of the total gas production rate. The 3D dust field is then calculated by propagating particles through the gas field by solving an equation of motion taking into account gas drag and nucleus gravity. We simulate the dust fields of particles in 40 discrete size bins ranging from 8 nm to 0.3 mm separately. A density integration along the camera line of sight through the coma gives the column densities that are translated into brightness values via a Mie scattering model. The results from the different dust size bins are weighted according to a dust size distribution function and combined into an artificial image that can be directly compared to OSIRIS images. The dust size distribution follows a power law function of the form n(r)~r-b, with n(r) being the number density, r the dust particle radius and b the power law index determining the steepness of the size distribution. For more details on the simulation model see also [2,6].
Acknowledgements
The team from the University of Bern is supported through the Swiss National Science Foundation under the grant 200020-178847 and through the NCCR PlanetS.
Calculations were performed on UBELIX (http://www.id.unibe.ch/hpc), the HPC cluster at the University of Bern.
OSIRIS was built by a consortium of the Max- Planck-Institut für Sonnensystemforschung, Göttingen, Germany; CISAS–University of Padova, Italy, the Laboratoire d’ Astrophysique de Marseille, France; the Instituto de Astrofísica de Andalucia, CSIC, Granada, Spain; the Research and Scientific Support Department of the European Space Agency, Noordwijk, The Netherlands; the Instituto Nacional de Tecnica Aeroespacial, Madrid, Spain; the Universidad Politechnica de Madrid, Spain; the Department of Physics and Astronomy of Uppsala University, Sweden; and the Institut für Datentechnik und Kommunikationsnetze der Technischen Universität Braunschweig, Germany. The support of the national funding agencies of Germany (DLR), France (CNES), Italy (ASI), Spain (MEC), Sweden (SNSB), and the ESA Technical Directorate is gratefully acknowledged.
References
[1] H. U. Keller, C. Barbieri, P. Lamy et al., 2007, Space Science Reviews 128, p. 433-506
[2] N. Thomas and H. Keller, 1990, Annales Geophysicae 8, p. 147-166
[3] S.-B. Gerig, R. Marschall, N. Thomas et al., 2018, Icarus 311, p. 1-22
[4] S.-B. Gerig, O. Pinzón-Rodríguez, R. Marschall et al., 2020 , Icarus (submitted)
[5] D. Bockelée-Morvan, V. Debout, S. Erard, 2015, A&A 583, A6
[6] R. Marschall, C.C. Su, Y. Liao et al., 2016, A&A 589, A90
How to cite: Gerig, S.-B., Pinzón-Rodríguez, O., Marschall, R., and Thomas, N.: Simulating nightside activity at comet 67P/Churyumov-Gerasimenko inferred from Rosetta/OSIRIS image analysis, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-587, https://doi.org/10.5194/epsc2020-587, 2020.
The European Space Agency's (ESA) Rosetta mission escorted comet 67P/Churyumov-Gerasimenko (hereafter 67P) from August 2014 to September 2016 along its orbit through the inner Solar System. It watched as the comet's activity started to develop at large heliocentric distances, come to its culmination at perihelion, and decline as the comet travelled out towards Jupiter's orbit. This long-term continuous monitoring of the comet's activity has provided an unprecedented wealth of data on this comet and its activity.
The observations revealed a complex bi-lobate shape [1, 2] and diverse morphology [3]. As a comet approaches the Sun it is heated and the ices start sublimating and ripping with them dust particles. Thus one of the important questions to be answered was what the bulk of the comet was made of i.e. what the bulk refractory-to-volatile ratio is. In the simplified view where any ejected material is lost to space two measurements are sufficient to determine this ratio. First, the total mass loss during one apparition measured by the Radio Science Investigation (RSI) [4]. Second, the total volatile mass loss which can be indirectly determined by the in-situ measurements of the gas density [5, 6, 7] or remote sensing data [8, 9, 10, 11]. In this simple case, the refractory-to-volatile ratio can be immediately inferred from those two measurements. But the complex surface morphology has revealed large dust deposits [12] that indicate that possibly a large fraction of the ejected dust is re-deposited [13]. If that is indeed the case, then the two above mentioned quantities cannot constrain the total dust mass ejected but rather only the dust mass escaping the nucleus gravity. Further, the process of dust fall-back obscures the emitted dust-to-gas ratio.
In this work, we present results that simultaneously constrain the dust size distribution, dust-to-gas ratio, fraction of dust re-deposition, and total mass production rates for comet 67P. We use a 3D Direct Simulation Monte Carlo (DSMC) gas dynamics code to simulate the inner gas coma of the comet for the duration of the Rosetta mission. The gas model is constrained by ROSINA/COPS data. Further, we simulate for different epochs the inner dust coma using a 3D dust dynamics code including gas drag and the nucleus' gravity. Using advanced dust scattering properties these results are used to produce synthetic images that can be compared to the OSIRIS data set. These simulations allow us to constrain the properties of the dust coma and the total gas and dust production rates.
In particular, we show how the dust-to-gas mass production rate ratio, the power-law exponent of the dust size distribution, the fraction of dust fall back, and the scattering properties of the dust are inter-related and constrain each other. Because these parameters are not independent they need to be fit simultaneously. E.g. the lowest mass needed to match the brightness of the dust coma as observed by OSIRIS is achieved with power-law distributions with exponents between 4 and 4.5. Using the constraint of the total mass loss of the comet during the 2015 apparition we will show that only a narrow parameter set fits all observations.
We determined a total volatile mass loss of (6.1 ± 1.5)·109 kg during the 2015 apparition. Further, we found that power-laws with q=3.7+0.57-0.078 are consistent with the data. This results in a total of 5.1+6.0-4.9 ·109 kg of dust being ejected from the nucleus surface, of which 4.4+4.9-4.2·109 kg escape to space and 6.8+11-6.8·108kg (or an equivalent of 14+22-14 cm over the smooth regions) is re-deposited on the surface. This leads to a dust-to-gas ratio of 0.73+1.3-0.70 for the escaping material and 0.84+1.6-0.81 for the ejected material. We have further found that the smallest dust size must be strictly smaller than ~30 μm and nominally even smaller than ~12 μm.
Acknowledgements
We thank Frank Preusker and Frank Scholten for providing us the comet shape model SHAP7 [2] used in this work.
We thank Vladimir Zakharov for providing valuable comments on the section of the analytical solution.
We acknowledge the personnel at ESA's European Space Operations Center (ESOC) in Darmstadt, Germany, European Space Astronomy Center (ESAC) in Spain, and at ESA for the making the Rosetta mission possible. Furthermore, we thank the OSIRS and ROSINA instrument and science teams for their hard work. We thank Martin Rubin and Kathrin Altwegg for giving us access and support to/for the ROSINA/COPS data.
References
[1] Sierks, H., Barbieri, C., Lamy, P. L., Rodrigo, R., Koschny, D., Rickman, H., et al. 2015, Science, 347, 1044
[2] Preusker, F., Scholten, F., Matz, K.-D., et al. 2017, A&A, 607, L1.
[3] Thomas, N., Davidsson, B., El-Maarry, M. R., Fornasier, S., Giacomini, L., Gracia-Berna, A. G., et al. 2015. A&A 583, A17
[4] Pätzold, M., Andert, T. P., Hahn, M., Barriot, J.-P., Asmar, S. W., Häusler, B., et al. 2019, MNRAS, 483, 2337–2346.
[5] Fougere, N., Altwegg, K., Berthelier, J. J., et al. 2016, A&A, 588, A134.
[6] Läuter, M., Kramer, T., Rubin, M., and Altwegg, K., 2018, MNRAS, 483, 852–861
[7] Combi, M., Shou, Y., Fougere, N., Tenishev, V., Altwegg, K., Rubin, M., et al., 2020, Icarus 335, 113421
[8] Migliorini, A., Piccioni, G., Capaccioni, F., Filacchione, G., Bockelée-Morvan, D., Erard, S., et al., 2016, A&A 589, A45.
[9] Bockelée-Morvan, D., Crovisier, J., Erard, S., Capaccioni, F., Leyrat, C., Filacchione, G., et al., 2016, MNRAS, 462 S170–S183
[10] Marshall, D. W., Hartogh, P., Rezac, L., von Allmen, P., Biver, N., Bockelée-Morvan, D., et al., 2017, A&A, 603, A87
[11] Biver, N., Bockelée-Morvan, D., Hofstadter, M., Lellouch, E., Choukroun, M., Gulkis, S., et al. 2019, A&A, 630, A19
[12] Thomas, N., El Maarry, M. R., Theologou, P., Preusker, F., Scholten, F., Jorda, L., et al., 2018, PSS, 164, 19–36
[13] Thomas, N., Sierks, H., Barbieri, C., Lamy, P. L., Rodrigo, R., Rickman, H., et al., 2015. Science, 347, 440
How to cite: Marschall, R., Markkanen, J., Gerig, S.-B., Pinzón-Rodríguez, O., Thomas, N., and Wu, J.-S.: The dust-to-gas ratio, size distribution, and dust fall-back fraction of comet 67P/Churyumov-Gerasimenko, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-375, https://doi.org/10.5194/epsc2020-375, 2020.
Abstract
We present results from a new 3D numerical code for solving the time-dependent equations of statistical equilibrium in cometary comae and planetary exospheres. This enables a more accurate calculation of the molecular excitation, for simulations of far-infrared and submillimeter emission lines. Our non-LTE radiative transfer code is based on the LIME (Line Modelling Engine) source code. It includes a robust 3D calculation of the internal radiation field and represents an improvement over the previous (steady-state) model for the case of rapidly expanding cometary atmospheres and planetary exospheres. Here we compare the results of the level population distributions for HCN and CO in a cometary coma using both time-dependent and steady-state solutions, and consider possible future applications to plumes from icy moons.
1. Introduction
The ability to accurately model astronomical observations in low-density environments, where local thermodynamic equilibrium cannot be assumed, is dependent on an accurate solution of the radiation transfer problem. Examples include the study of cometary volatiles, icy moon atmospheres, outflows, and young stellar objects. Furthermore, spacecraft missions and ground-based telescope facilities such as the Atacama Large Millimeter-submillimeter Array (ALMA) allow for very high-resolution astronomical observations, which require detailed models capable of handling the interaction between multiple molecular species in arbitrary geometries.
LIME (Line Modeling Engine) is a non-LTE, 3D radiative transfer code for submillimeter to far-infrared emission, introduced in 2010 [1]. In addition to transitions due to collisional excitation and spontaneous radiative decay, LIME also simulates transitions due to radiative excitation and radiation trapping via a 3D Monte Carlo treatment of the radiation field. However, the efficacy of LIME, and similar methods, for dynamic environments including expanding (cometary) atmospheres is limited, since the equations of statistical equilibrium are solved as a function of spatial coordinates using the assumption of steady-state. We have built upon the LIME codebase to create a new module that dispenses with the assumption of steady-state by implementing a time-dependent solution for the gas trajectories, following the formalism in reference [2]. In addition to being capable of performing the full 3D treatment of the radiation field, it also provides the option of using the escape probability (Sobolev’s) method [2]. While less accurate than the Monte Carlo photon trapping method, the escape probability method provides a less computationally demanding alternative, ideal for fast calculations or situations where radiation trapping does not play a significant role. Our new model also includes electron collisional transitions, which can be particularly important in cometary comae.
2. Equations of statistical equilibrium
The time-dependent evolution of the level populations is given by the coupled differential equations
where pij is the transition rate from level i to j, and ni is the fractional population of level i. In the case of steady-state, the left-side of the equation is set equal to zero. The transition rates are given by
where Cij denotes the collisional transitions from level i to j, Bij is the induced emission or absorption rate, Aij is the spontaneous emission rate, and Jij is the radiation mean intensity averaged over 4π and integrated over the line. When the escape probability (Sobolev’s) approximation is used, equation (2) is simplified to
where βij is the photon escape probability. For a more detailed description of the transition rate terms, see references [2, 3].
3. Method
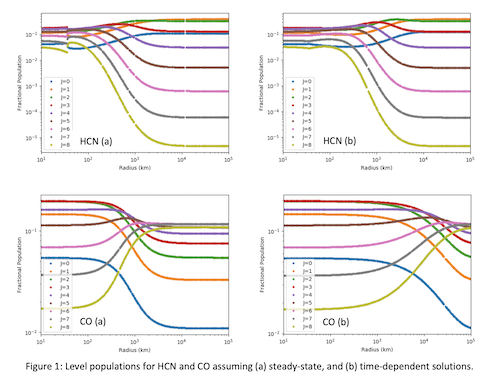
We consider two models for a uniformly-expanding H2O-dominated cometary coma: one with an HCN abundance of 0.1% (photodissociation rate βHCN = 1.5 × 10-5), and another with a CO abundance of 5% (βCO = 7.5× 10-7). Table 1 contains the parameters that are common to both models. The collisional transition rates with water were retrieved from the LAMDA database [4], assuming Cij (H2O) = Cij (H2). Electron collisional rates were calculated following the formalism in reference [3]. The coma outflow is followed from the nucleus (r = 2.5 km) out to 105 km. The fractional energy level populations (as a function of rotational quantum number J) were calculated using (a) the steady-state and (b) the time-dependent methods. Results for J = 0 to 8 are shown in Figure 1.
4. Results
5. Summary
The level populations undergo a characteristic evolution from LTE in the collisional-dominated regime close to the nucleus, towards fluorescence equilibrium in the outer coma. The dynamical effects included in the time-dependent treatment (panels b) are evident through the delayed onset of the departure from LTE as a function of radius, which occurs due to the dynamical (outflow) timescale being less than the excitation timescale. Consequently, the time-dependent model provides more accurate results than the steady-state model, particularly in the case of low H2O production rates, where departure from LTE occurs too close to the nucleus if steady-state is assumed. The effect is more pronounced for CO due to its longer radiative lifetime. This effect should therefore be taken into account in future models for expanding cometary comae and icy moon exospheres.
6. References
[1] C. Brinch and M. R. Hogerheijde. A&A, 523, A25, 2010.
[2] D. Bockelee-Morvan. A&A, 181, 169, 1987.
[3] V. Zakharov et al. A&A, 473, 303, 2007.
[4] Schöier, F.L., van der Tak, F.F.S., van Dishoeck E.F., Black, J.H., A&A, 432, 369, 2005.
How to cite: Garcia-Berrios, E., Cordiner, M. A., Charnley, S. B., de Val-Borro, M., and Biver, N.: A 3D, time-dependent, non-LTE radiative transfer code for radio and far-infrared observations of cometary comae and planetary exospheres, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-426, https://doi.org/10.5194/epsc2020-426, 2020.
Please decide on your access
Please use the buttons below to download the presentation materials or to visit the external website where the presentation is linked. Regarding the external link, please note that Copernicus Meetings cannot accept any liability for the content and the website you will visit.
Forward to presentation link
You are going to open an external link to the presentation as indicated by the authors. Copernicus Meetings cannot accept any liability for the content and the website you will visit.
We are sorry, but presentations are only available for users who registered for the conference. Thank you.

