Poster presentations and abstracts

Introduction

Mawrth Vallis is generally considered to be the oldest of Mars’ outflow channels [1]. It incises Noachian (> 3.7 Ga) terrain and is associated with thick (> 150 m), clay-bearing deposits [2]. Clays are important astrobiologically because they are potential catalytic substrates for (pre)biotic chemistry [3] and have a high potential to preserve biosignatures [4]. The presence of clay-bearing deposits was an important factor in the decision to shortlist an area adjacent to Mawrth Vallis as a candidate landing site for the ExoMars “Rosalind Franklin” rover [5], whose mission is to search for signs of ancient life on Mars [6]. Ultimately, Mawrth Vallis was not selected as the ExoMars landing site.

The origin and geological context of the clay-bearing deposits is not well understood [7]. Furthermore, the geomorphology of Mawrth Vallis, which records its history of deposition/burial and erosion/exhumation, is also less well-studied compared with its mineralogy. Here, we present our ongoing geological mapping of Mawrth Vallis, which we are conducting to investigate the relationship between the channel and the clay-bearing deposits. We are producing a detailed map of the main Mawrth Vallis channel adjacent to the proposed ExoMars landing ellipse. We will also produce an accompanying geomorphic feature map along the whole length of Mawrth Vallis at a smaller scale.

We are creating this map as part of the Planmap project [8], which aims to provide standards for European researchers to adhere to in order to aid the dissemination of their maps. Planmap is producing exemplar maps of Mercury [e.g. 9], the Moon [e.g. 10], and Mars [e.g. this work], where various datasets (visual images, elevation models, spectra, crater size-frequency distributions) will be fused to make more fully-intergrated geological maps. The abundance and diversity of data types at Mawrth Vallis, in addition to its scientific interest, make this region particularly suitable for Planmap.

Data

We are using a ~6 m/pixel orthorectified CTX [11] mosaic basemap, supplemented by 25–50 cm/pixel HiRISE images [12], ~4 m/pixel colour CaSSIS images [13], and ~20 m/pixel CTX digital elevation models (DEMs).

Methods

We are mapping using ArcGIS 10.6.1. Mawrth Vallis spans 340°E–247°E and 18°N–26°N. We are mapping in a stereographic projection centred on 343°E, 22.4°N. We are digitising the main map on the CTX mosaic at 1:20,000-scale (~full CTX resolution), and intend to publish the map at ~1:100,000-scale. The geomorphic feature map will be published alongside the main map. We will use HiRISE and CaSSIS images to aid unit definition and CTX DEMs to aid stratigraphic interpretation.

Results and future work

Figure 1 shows the current state of our map.

We plan to begin work on the geomorphic feature map soon. Progress on the main map will continue in parallel. We will investigate the stratigraphic position of Mawrth Vallis relative to the large impact craters in the region. We will consider how the stubby depressions that occur with the main channel’s walls formed.

Acknowledgements

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 776276.

References

[1] Ivanov and Head (2001) J. Geophys. Res., 106, 3275–3295. [2] Loizeau et al. (2007), J. Geophys. Res. Planets, 112, E8. [3] Hazen and Sverjensky (2010), CSH Perspect. In Biol., 2, a002162. [4] Farmer and Des Marais (1999), J. Geophys. Res. Planets, 104, 26977–26995. [5] Poulet et al. (2020), Astrobiology, 20, 199–234. [6] Vago et al. (2017), Astrobiology, 17, 471–510. [7] [8] Massironi et al. (2018), Geophys. Res. Abs., 20, EGU2018-18106. [9] Wright et al. (2019), J. Maps, 15, 509–520. [10] Pöhler et al. (2020) Europ. Lunar. Sym., Abstract. [11] Malin et al. (2007), J. Geophys. Res. Planets, 112, E5. [12] McEwen et al. (2007), J. Geophys. Res. Planets, 112, E5. [13] Thomas et al. (2017), Space Sci. Rev., 212, 1897–1944.

How to cite: Wright, J., Balme, M., Davis, J., Fawdon, P., and Rothery, D.: Geological mapping of Mawrth Vallis, Mars, by PLANMAP, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-807, https://doi.org/10.5194/epsc2020-807, 2020.

Virtual Reality (VR, with headsets) and Augmented Reality (AR, using a smartphone or tablet) coupled with 3D photogrammetric reconstructions are increasingly used for science, education and outreach applications. These techniques are not new [e. g. 1, 2], but they are becoming progressively more widespread thanks to the release in 2016 of technologically mature and cost-effective hardware solutions accessible to the general public. In the field of planetology, VR and AR theoretically allow the possibility to simulate field trips to remote places that are otherwise inaccessible to humans. Using high-resolution imaging, coupled with spectral or morphological data gathered by robotic explorers (orbiters, landers, rovers), we can create integrated virtual environments that accurately represent the surface of planetary bodies and allow the cross-comparison of different datasets. These virtual environments provide the possibility to navigate on a global scale using orbital data, and move down to the surface when in situ data are available to visualize and analyze local outcrops. This is particularly the case of the Moon and Mars, where both extensive remote and groundtruth data are available [3, 4, 5].

We are investigating how the information from various sources can be combined in a comprehensive way to display, manipulate, analyze and share both analytical data and results. We have for example integrated visible high-resolution imagery, digital elevation and outcrop models, geomorphological maps and compositional maps derived from spectroscopic measurements on several test sites such as the Copernicus crater and Apollo 17 landing site on the Moon, the Crommelin crater and Kimberley area (Gale crater) on Mars, and the Hokusai quadrangle area on Mercury. The VR and/or AR rendering of simple orbital and/or ground-based 3D models can be performed using a web-based solution such as Sketchfab (e.g. https://sketchfab.com/LPG-3D or https://sketchfab.com/planmap.eu), offering the possibility to visualize, interact, and share medium-resolution 3D versions of these multi-scale data (Fig. 1a and 1b). The use of a more powerful and versatile solution based on a game engine [6] allows the development of more complex solutions, for example dedicated measurement tools (Fig. 1c) or multi-layering capabilities (Fig. 1d). These approaches offer new possibilities in terms of data exploration, analysis, and applications for research and education during “virtual planetary field-trips”.

Acknowledgments: This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 776276 (PLANMAP).

 References :  

[1] McGreevy (1993), M.W. Virtual reality and planetary exploration. In Virtual Reality; Elsevier: Amsterdam, The Netherlands,; pp. 163–197, ISBN 0-12-745045-9.

[2] Favalli, M. et al. (2012), Multiview 3D reconstruction in geosciences. Comput. Geosci. 2012, 44, 168–176.

[3] Ostwald, A.; Hurtado, J. 3D models from structure-from-motion photogrammetry using MSL images: Methods and implications. In Proc. of the 48th LPSC, The Woodlands, TX, USA, 2017. LPI Contribution No. 1964, id.1787.

[4] Caravaca, G. et al. (2020) Planet Space Sci, 182, 104808, DOI: 10.1016/j.pss.2019.104808

[5] Le Mouélic, S. et al. (2020) Remote Sensing, 12 (11), DOI: 10.3390/rs12111900

[6] Nesbit, P.R et al. (2020), GSA Today, vol. 30, 4–10. DOI: 10.1130/GSATG425A.1

How to cite: Le Mouélic, S., Caravaca, G., Mangold, N., Wright, J., Carli, C., Altieri, F., Zambon, F., Van Der Bogert, C., Pozzobon, R., Massironi, M., Pio Rossi, A., and De Toffoli, B.: Using Virtual and Augmented Reality in Planetary Imaging and Mapping – a Case Study, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-589, https://doi.org/10.5194/epsc2020-589, 2020.

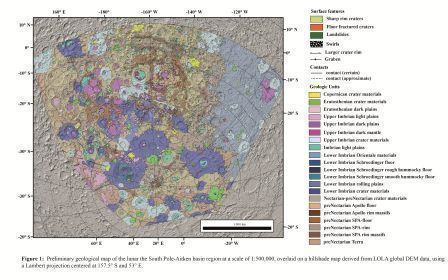
Introduction:  The lunar South Pole-Aitken basin (SPA) is of special interest for human and robotic missions for the near future [e.g. 1–4]. This makes detailed studies of the geological background and setting of the region a high priority. Located on the lunar farside, centered at ~53° S, 191° E, SPA basin is the largest and likely the oldest lunar basin [5-7]. The region is widely influenced by rays of the ~3.85 Ga old Orientale basin [8].

In this study, we constructed a geologic map of the full extent of the SPA basin, covering the South Pole, and extending eastward to include part of the Orientale basin (Fig. 1). Altogether, this provides a comprehensive overview of the geology of the region.

Methods:  This map, which is an extension of an Apollo basin map [9], was done as part of the PLANetary MAPping (PLANMAP - H2020 n°776276) project (https://planmap.eu/). For large scale mapping, we used the Lunar Reconnaissance Orbiter (LRO) Wide-Angle Camera (WAC) basemap (100 m/pixel). For more detailed, smaller areas, and for identifying specific features, we used LRO Narrow-Angle Camera (NAC; 0.5 m/pixel) [10] and Kaguya (10 m/pixel) data with different incidence angles. We also used a hybrid spectral mapping technique using Clementine [11], M³ [12] and Kaguya MI [13] data. The topographic features were mostly mapped using Lunar Orbiter Laser Altimeter (LOLA) digital elevation models (DEMs) and a LOLA/Kaguya merged DEM with a resolution of 59 m/pixel [14]. To reduce shadows, particularly in the southernmost latitudes, we produced hillshade maps with various illumination conditions. We used PLANMAP mapping standards [15], which are based on USGS standards [16].

We identified units using morphological appearance and albedo contrasts. The mapping scale is 1:500,000. For the purpose of determining the stratigraphic relationships, we first established the relative ages of units using morphological evidence. For an absolute stratigraphy, we then performed crater size-frequency distribution (CSFD) measurements for fitting of absolute model ages (AMAs) using the production and chronology functions of [17]. CSFD measurements were made using CraterTools [18] in ArcGIS, and we fit the AMAs with Craterstats [19]. Detailed descriptions of the CSFD measurement technique are given by [17, 20]. The Apollo basin map is currently available on the PLANMAP website (https://data.planmap.eu/pub/moon/PM-MOO-MS-SPAApollo/) and the map of SPA will be available shortly.

Geology: In our study area, we defined three classes of geologic features: Basin materials, crater materials, and plains-forming materials. Basin materials are related to the formation of the large basins in the area with the oldest and most dominant being the SPA. We also specifically identified materials related to Apollo, Schrödinger, and Orientale Basins. Crater materials are divided into different classes according to the state of degradation and shape of the craters. For achieving a framework for the absolute chronology, we determined AMAs for several key craters. Plains-forming materials are characterized by their relatively flat, smooth surfaces and can be further divided into dark and light plains based on their albedo. Furthermore, we observed dark mantle material, which might be originate from pyroclastic volcanic events. These mantle materials occur most prominently in Schrödinger and Oppenheimer craters.

The SPA basin rim is obscured by various later impacts and is degraded due to its old age. The most distinctive appearance of the SPA basin rim is in the NW quadrant, close to the Apollo basin. Here, we identified two topographic rings of SPA basin rim massifs. Around the South Pole, image quality is lower and features become obscured by the low sun angle. We were able to find traces of the outer massif, but most of the inner massif is hidden below younger craters. The whole region is large influenced by the Orientale basin-forming impact, resulting in large quantities of ejecta-covered terrain and secondary cratering across the entire SPA basin.

Acknowledgments: This paper is part of a project that has received funding from the European Unions Horizon 2020 research and innovation programme under grant agreement Nº776276 (PLANMAP).

References: [1] Flahaut et al. (2019) PSS., in press. [2] Steenstraet al. (2016) Adv. Space Res. 58, 1050–1065. [3] Allender et al. (2018) Adv. Space Res. 63, 692–727. [4] Hiesinger et al. (2019) LPSC 50, 1327. [5] Garrick-Bethell and Zuber (2009) Icarus, 204, 399–408. [6] Hiesinger et al. (2012), LPSC 43, 1659. [7] Fortezzo et al. (2020), LPSC 51, 2760. [8] Stuart-Alexander (1978) USGS Map I-1047. [9] Ivanov et al. (2018) JGR Planets, 123, 2585–2612. [10] Robinson et al. (2010) Space Sci. Rev., 150, 81–124. [11] Pieters et al. (1994). Science, 266, 1844–1848. [12] Isaacsom et al. (2013). JGR, 118, 369–381. [13] Ohtake et al (2013) Icarus, 226, 364–374. [14] Barker et al. (2016) Icarus, 273,346-355. [15] wiki.planmap.eu/display/public/D2.1-public. [16] FGDC (2006). FGDC-STD-013-2016. [17] Neukum et al. (2001) Space Sci. Rev. 96, 55–86. [18] Kneissl et al. (2011) PSS, 59, 1243–1254. [19] Michael and Neukum (2010) EPSL, 294, 223–229. [20] Hiesinger et al. (2000) JGR, 105, 29239–29276.

How to cite: Poehler, C. M., Ivanov, M. A., van der Bogert, C. H., Hiesinger, H., Iqbal, W., Pasckert, J. H., Wright, J., and Head, J. W.: The Lunar South Pole-Aitken Basin Region: A New Geological Map , Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-600, https://doi.org/10.5194/epsc2020-600, 2020.

South Polar Aitken (SPA) is the largest and deepest basin on the Moon [1, 2], and several regions within this widespread basin have been considered as possible landing sites for present and future missions. Some of these sites are also targets of the H2020 n° 776276- PLANMAP project [3]. In this work, we focus on specific areas within SPA, Apollo basin, Lebinitz and Von Karman craters regions (see fig. 1). For our analysis, we considered the M³/Chandrayaan-1 data [4], after the application of the last calibration, thermal removal and photometric correction [5, 6].

SPA is rich in high Ca-pyroxenes, except for some central crater peaks, where low Ca-pyroxenes dominate, and no extensive olivine-rich areas are observed [1, 7, 8]. Based on the spectral characteristics on the M³ spectra, we define specific spectral parameters, such as band centers, depths, spectral slopes, including selected RGB color composite combinations [5]. These indices are the starting point for retrieving the spectral units of the regions considered. The final aim of this work is to find a link between spectral, and morpho-stratigraphic units [9] to reach out highly informative geological maps of the Moon. This innovative approach holds the efforts of different research units and is one of the main goals of the PLANMAP project.

References: [1] Ohtake, M. et al., 2014, GRL. [2] Moriarty, D.P. et al., 2018, JGR. [3] https://www.planmap.eu/, [4] Pieters et al., 2009, Current Science., [5] PLANMAP D4.3- Spectral Indices and RGB maps. [6] Besse, S. et al., 2012, Icarus. [7] Dhingra, D., 2018, Geosciences. [8] Melosh, H. J., et al., 2017, Geology. [9] Ivanov, M.A., 2018, JGR.

Acknowledgments: This work is funded by the European Union’s Horizon 2020 research grant agreement No 776276- PLANMAP.

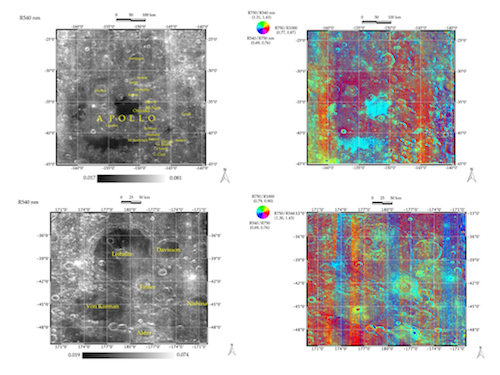
Figure 1: Apollo basin (top-left) and Leibnitz and Von Karman craters (bottom-left) reflectance map at 540 nm. Apollo basin (top-right) and Leibnitz and Von Karman craters (bottom-right) Clementine-like mosaic derived by M³ data (bottom-right).

How to cite: Zambon, F., Carli, C., Altieri, F., Combe, J.-P., van der Bogert, C. H., Pöler, C., Hiesinger, H., Le Mouélic, S., Mangold, N., Caravaca, G., and Massironi, M.: Spectral and morpho-stratigraphic units integration on Apollo basin and Leibnitz/Von Karman craters on the Moon, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-905, https://doi.org/10.5194/epsc2020-905, 2020.

Geological maps have been historically a central part of the geological knowledge acquisition process: they are used to summarize all the relevant information of a site of interest and they provide the cornerstone for decision making, scientific discovery and three-dimensional geological modeling.

Depending on the scope of the geological survey the cartography can depict different types of content: whether lithostratigrapy, chronostratigrapy, morphology, or other criteria are considered, the building blocks of a geological map is the geological unit, as the base element used to subdivide a region into geologically homogeneous patches of terrain. Digitized maps are normally represented within GIS software as polygonal layers.

A common approach for mapping has been to directly draw polygons representing the different units on the map: although this approach appears the simplest one, it poses several issues in terms of topological consistency of resulting maps, especially when it comes to updating existing cartography. Furthermore, from a purely information science standpoint this representation, although useful for visualization, is inherently redundant, defining the same boundary geometry two times for each polygonal couples in contact.

Editing polygonal layers is inherently problematic because vertex and edge correspondence between polygons in contact must be enforced by the operator. Although most GIS software implements appropriate tools (for editing and  for topology validation) which can help in achieving error-free polygonal layers, the burden of using them is left to the operator and it is not enforced by the data format itself.

A better solution for generating topologically-consistent geological maps consists in tracing the contacts separating the units, and then transforming them into polygonal layers (by using what is often known as a “polygonize” operation) for map finalization (see Figure 1).

Figure 1: Generation of a consistent polygonal layer by polygonize operation, this can be performed by any GIS and is suggested as a good practice in geological map generation. A line layer is used for tracing the contacts between the different units and a point layer is also needed to define attributes for the polygons.

This approach is also more similar to the geological reasoning that is performed when mapping, especially when remotely -sensed imagery is used (as in planetary mapping): the operator tries to identify the boundaries between different terrains rather than directly defining the area covered by the units themselves. This strategy hasve the clear benefit of making editing the map easier but, even when employed by the operator, the original layers (contact lines and points) are rarely or never distributed to the public, making it impossible to apply this method when updating already existing maps.

In order to solve this problem we implemented a python module and a QGIS plugin called Mappy which is mostly based on already-existent modules as numpy (Oliphant 2006), geopandas (Jordahl et al. 2019), and topojson (Bostock 2017). Mappy implements the backwards transformation of the polygonize operation decomposing a polygonal layer into boundary lines and a point layer that contains the attributes of the original polygonal layer (the forward transform is also implemented). 

The input polygonal layer is first transformed into a topology-aware representation via topojson: first the intersection points are detected and then the polygons boundaries are split at those points, creating a list of arcs: each representing an unique portion of a contact line (Figure 2). Topojson representation can also account for rounding errors in the nodes coordinates and makes it possible to also consistently apply line-simplification methods (e.g. to reduce the number of nodes) while maintaining the original topology.

Figure 2: The inverse operation of a "polygonize" operation as performed by mappy. a) the input polygonal layers with attributes; b) the topojson representation as list of arcs (each polygon is then just a list of arcs in the right order); c) the arcs are aggregated to create a representation more suitable for geological editing; d) point are positioned in the visual center of each polygon and the attributes are then transferred.

Although being topologically sound, the topojson format of a polygonal layer is not the best suited representation for editing geological maps: given each line is split at the intersection points (Figure 2b) a contact might be split in a number of segments (i.e. when a contact separates one unit from several others) making it more difficult to edit the contact of a specific unit. For this reason, Mappy further processes the lines to aggregate several continuous arcs into a single polylines (Figure 2c).

For each polygon an indicator point is then automatically computed to be in its visual center and the original attributes of the polygons are transferred to it. The points are placed by using the “polylabel” method provided by shapely module (Gillies and others 2007).

The described approach has been then implemented in a standalone module that is also accessible from a QGIS plugin enabling easy transformation of any existing map into a line and points representations and vice-versa, therefore simplifying the process of editing and topology checking of existent geological maps.

Acknowledgments: This research was supported by European Union’s Horizon 2020 under grant agreement No 776276- PLANMAP.

References:

Bostock, Mike, 2017 TopoJSON. URL: https://github.com/topojson/topojson-specification.

Gillies, Sean, and others, 2007 Shapely: Manipulation and Analysis of Geometric Objects. toblerity.org. https://github.com/Toblerity/Shapely.

Jordahl, Kelsey, Joris Van Den Bossche, Jacob Wasserman, et al., 2019 Geopandas/Geopandas: V0.4.1. Zenodo. https://zenodo.org/record/2585849, accessed June 29, 2020.

Oliphant, Travis, 2006 NumPy: A Guide to NumPy. https://www.numpy.org/.

How to cite: Penasa, L., Frigeri, A., Pozzobon, R., Brandt, C. H., De Toffoli, B., Naß, A., Rossi, A. P., and Massironi, M.: Constructing and deconstructing geological maps: a QGIS plugin for creating topologically consistent geological cartography, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-1057, https://doi.org/10.5194/epsc2020-1057, 2020.