SB7
Session assets
1 Introduction
The polarimetric properties of airless Solar System bodies provide invaluable insights into their surface characteristics. While extensively applied to asteroids, often interpreted using empirical models, the Moon – our most meticulously studied airless body – offers a unique "ground-truth" calibrated benchmark. Historical lunar polarimetry established fundamental relationships [1,2,3]. This study focuses on the geologically diverse Atlas crater region, treating its terrains as distinct analogues for asteroid surfaces. We employ a multi-step approach: first, fitting an empirical model typically used for Near-Earth Asteroids (NEAs) to characterize phase curve behavior and extract key parameters; second, applying Principal Component Analysis (PCA) to this set of derived and fitted parameters to identify dominant modes of variation; and third, utilizing machine learning for terrain segmentation based on these PCA components. This work aims to: (1) derive robust polarimetric parameters and identify distinct polarimetric units within Atlas using four spectral bands (B,V,R,I); (2) enhance understanding of how lunar surface properties (e.g., soil maturity, pyroclastic deposits) govern these signatures; and (3) provide a well-constrained calibration dataset for interpreting polarimetric observations of asteroids.
2 Methods
Spectropolarimetric observations of the Atlas crater region were acquired in the Johnson-Cousins BVRI filter bands. The instrumentation included a 430mm reflector telescope located at Mount Abu, India, and a 200mm reflector telescope at Wetter, Germany. The camera system employed, as detailed in [4], provided an image scale of approximately 0.9 km/pixel. The data capture the degree of linear polarization (DoLP) as a function of phase angle (α) across these four spectral bands.
1. Empirical Phase Curve Modeling: We applied the empirical phase-polarization model described for NEAs by Bagnulo et al. [5, Section 2.2, Equation 7]: DoLP(α)=A· sinB (α) · cosC (α/2) · sin(α − αinv). This model was fitted to the observed DoLP phase curves for sub-regions within the Atlas study area (example in Fig. 1).
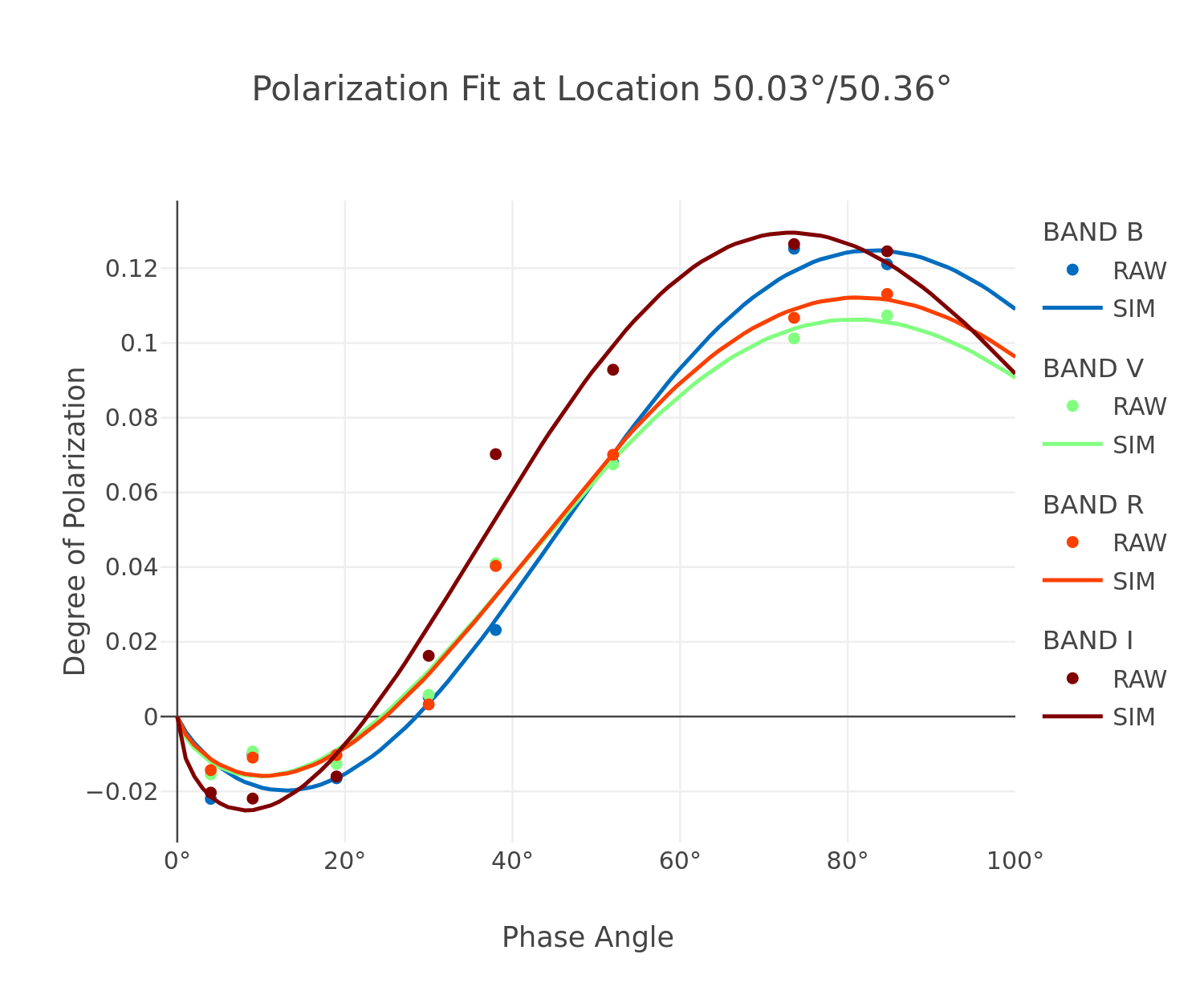
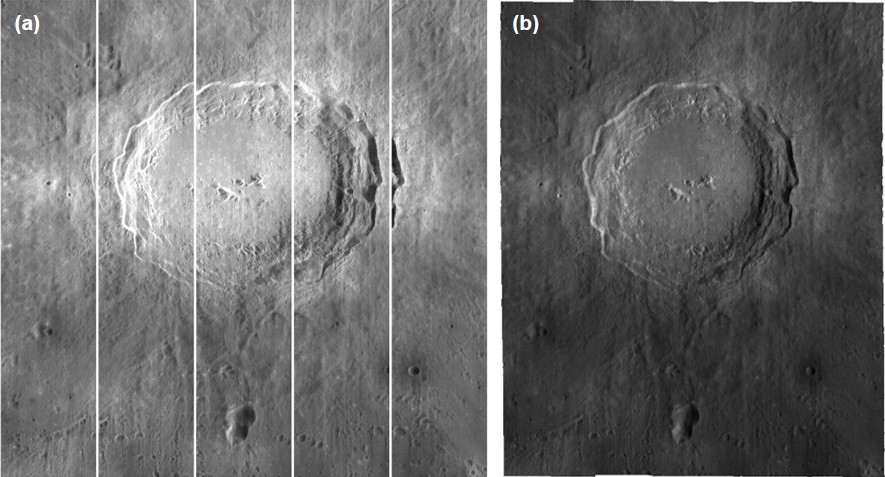
Figure 1 (Highland)
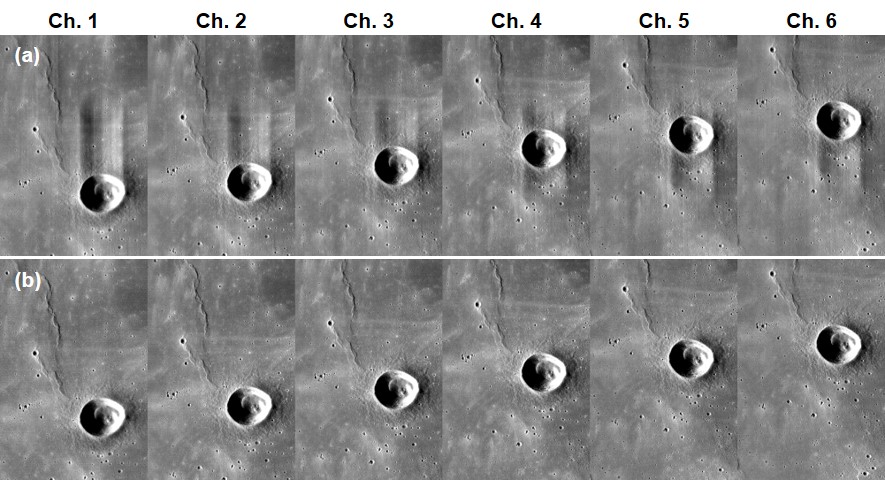
This yields maps of the fitted model parameters A, B, C, and αinv (Fig. 2). From these best-fit curves, features like minimum/maximum polarization (Pmin, Pmax) and their respective phase angles (αmin, αmax) were also numerically derived (Fig. 3).
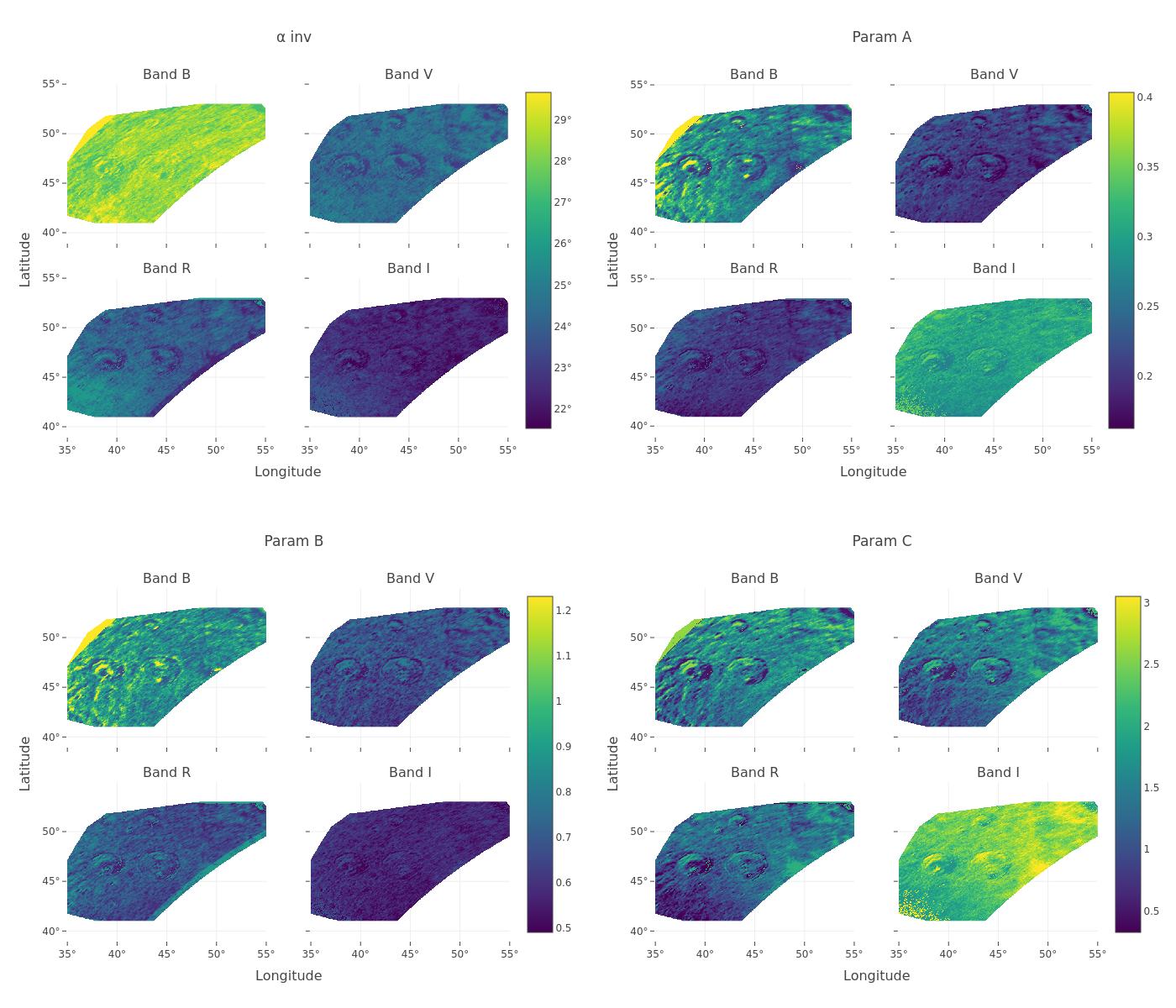
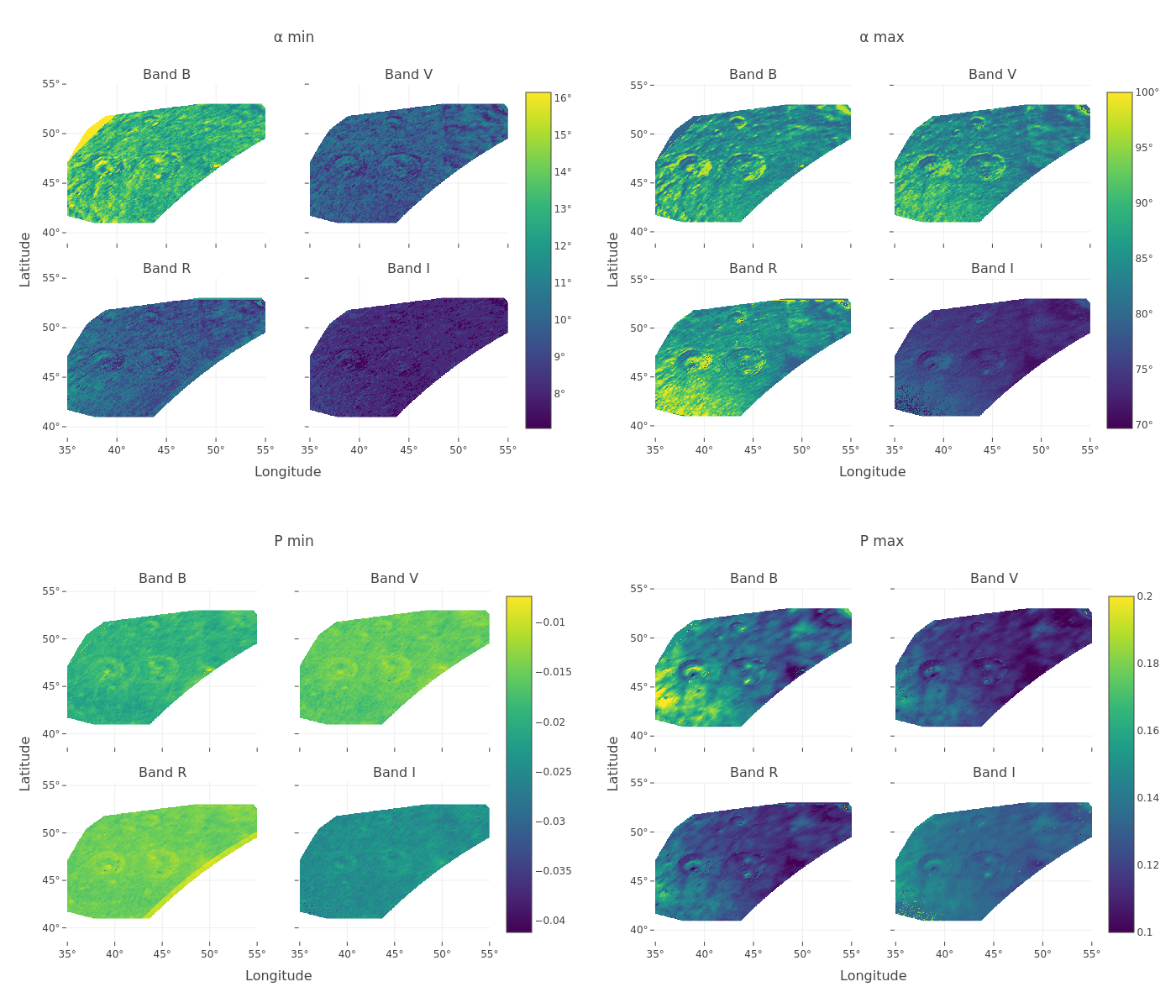
Figure 2 Figure 3
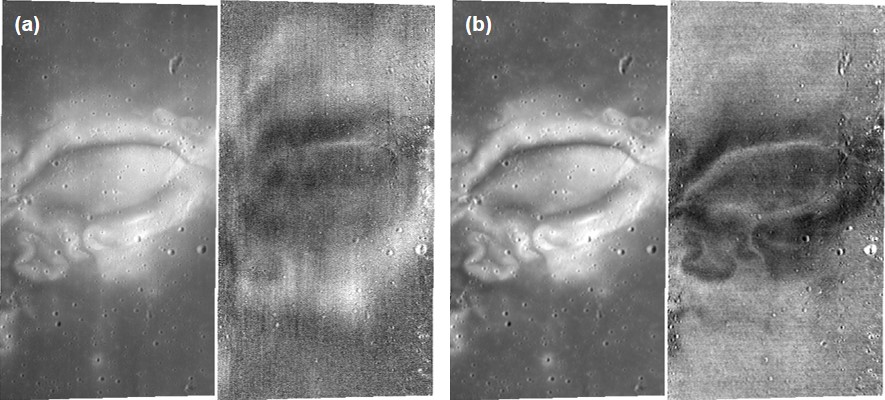
2. Principal Component Analysis (PCA) of Parameters: PCA was subsequently performed on the combined set of these eight parameters (four fitted: A, B, C, αinv; and four derived: Pmin, αmin, Pmax, αmax) obtained for each pixel across the BVRI bands. This approach reduces the dimensionality of the parameter space and identifies the principal axes of variation in the collective polarimetric response characteristics (Fig. 4).
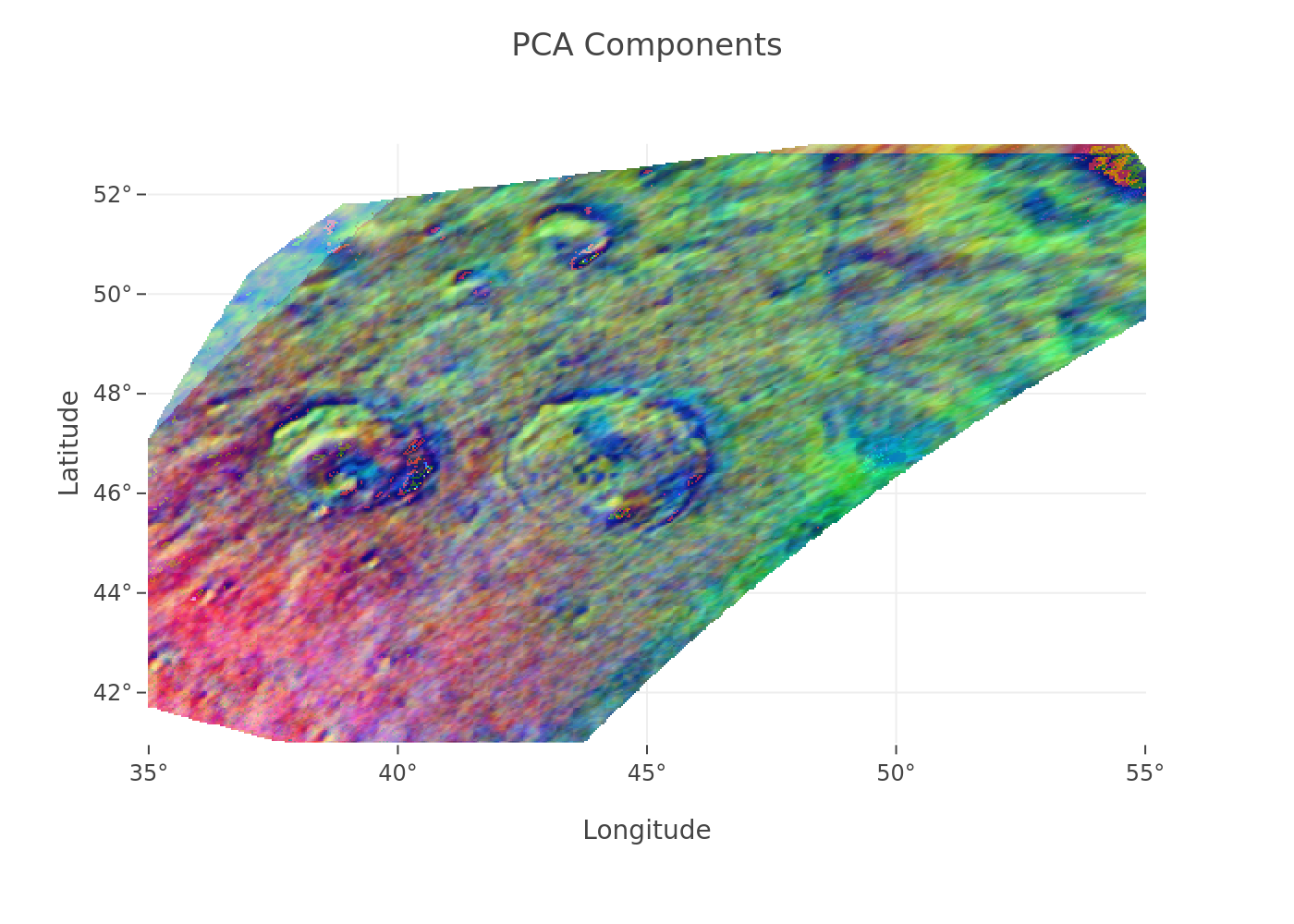
Figure 4
3. Clustering: Unsupervised machine learning (Gaussian Mixture Model clustering) was applied to the significant PCA components derived from the
parameter set. This step segments the Atlas region into distinct units based on similarities in their comprehensive polarimetric parameter signatures (Fig. 5).
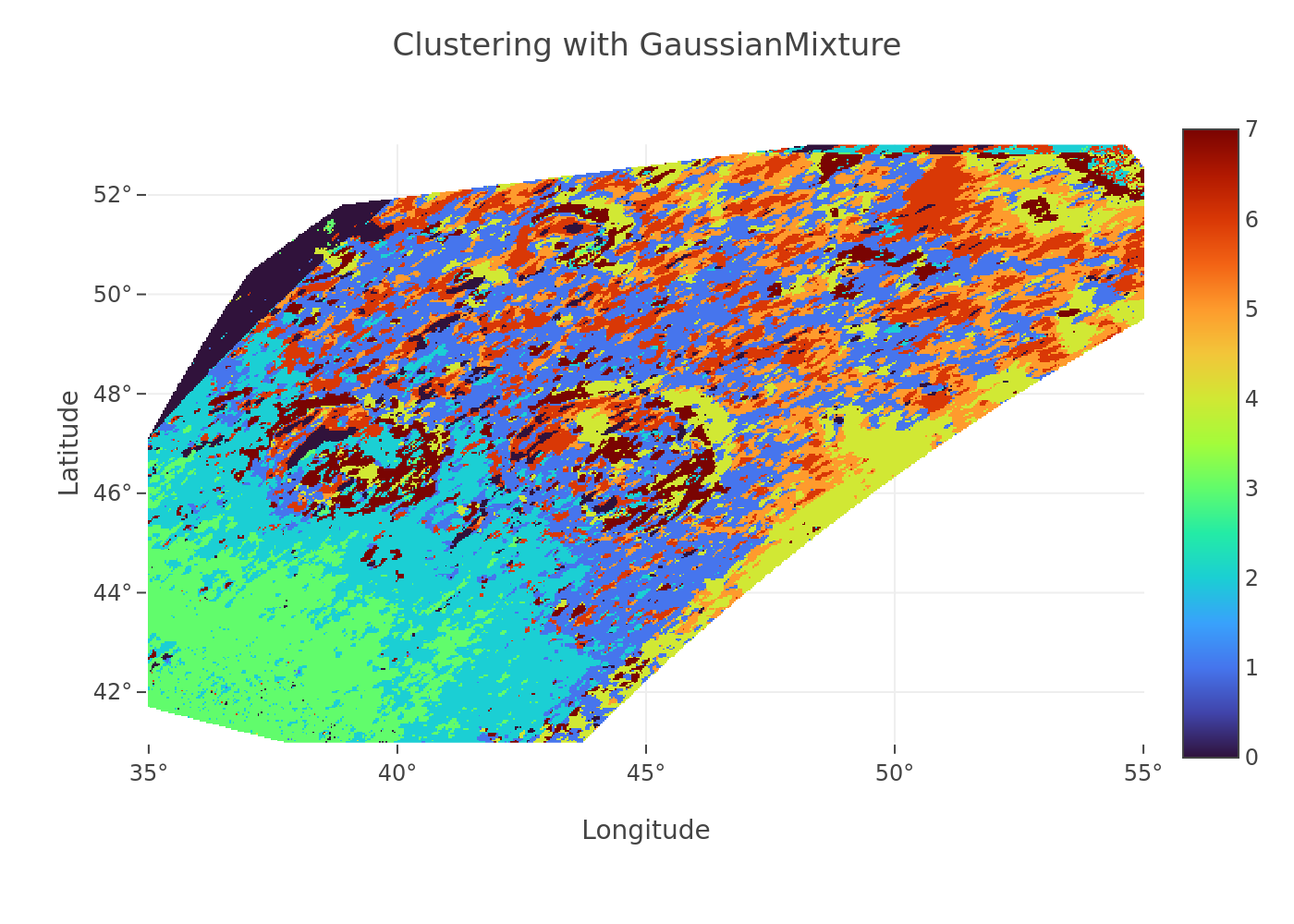
Figure 5
3 Results
The integrated analysis of the Atlas BVRI spectropolarimetric dataset yields several key findings:
1. Empirical Model and Derived Parameter Maps: The spatial maps of the fitted parameters (A,B,C,αinv, Fig. 2) and the derived polarimetric features (Pmin,αmin,Pmax,αmax, Fig. 3) exhibit apparent variations correlated with known geological units. Notably, higher αmax values are observed for more mature mare surfaces compared to the fresh ejecta of Atlas crater, consistent with Shkuratov et al. [6] linking higher αmax to increased soil maturity.
2. PCA of Parameter Space: The PCA components map (Fig. 4), derived from the comprehensive set of eight fitted and derived parameters, effectively highlights geological distinctions and interdependencies between these parameters. Different colors in the PCA map correspond to distinct combined polarimetric characterizations.
3. Clustering Results: The Gaussian Mixture Model clustering applied to the PCA components of the parameter set (Fig. 5) successfully segments the Atlas region into distinct units. A strong spatial correlation is observed between specific clusters and known pyroclastic deposits, on the floor of the Atlas crater. This indicates that the combined polarimetric parameters captured by PCA are sensitive to such deposits, yielding results for terrain differentiation similar in utility to the direct DoLP analysis in Wöhler, et al. [4].
4. Wavelength Dependencies: All initial parameters demonstrate noticeable dependencies on wavelength across the BVRI bands, which are propagated into the PCA and clustering stages.
4 Discussion
The Atlas region serves as an exceptional natural laboratory. By first parameterizing the phase curve behavior using an empirical model (Figs. 2,3), we distill the polarimetric information into a set of physically meaningful (though empirical) coefficients and features. The subsequent PCA on this parameter space (Fig. 4) identifies the dominant combinations of these characteristics that differentiate lunar terrains. The observed correlation between higher αmax values and increased soil maturity provides a quantitative lunar benchmark. Critically, the clustering of these PCA-reduced parameters (Fig. 5) demonstrates a powerful capacity to identify and map geological units, the pyroclastic deposits. Although the PCA is applied to a different input dataset than in Wöhler, et al. [4] (parameters vs. raw DoLP), the ability to distinguish terrains, including pyroclastics, remains robust, suggesting that the information content is well-preserved and effectively summarized by the empirical model parameters.
5 Conclusion
This study demonstrates a novel approach by combining empirical phase curve modeling with PCA of the resulting parameter set and subsequent machine learning to analyze BVRI lunar spectropolarimetric data from the Atlas region. We have quantitatively characterized phase curve behavior and identified distinct polarimetric units defined by combinations of these parameters, linking them to geological features and surface properties like soil maturity and pyroclastic deposits. These findings establish the Atlas region as a crucial calibration site for interpreting asteroid polarimetry, and the methodology offers a new avenue for extracting comprehensive insights from polarimetric datasets.
[1] Lyot,Ph.D.Thesis,Jan.1929.
[2] Dollfus,Planets&Satellites.Jan.1961,p.343.
[3] Shkuratov et al.,PSS59.13(Oct.2011),pp.1326–1371.
[4] Wöhler et al., AJ167.5(May2024),p.187.
[5] Bagnulo, et al.,A&A32.1(Dec.2024)
[6] Shkuratov et al., Icarus187.2(Apr.2007),pp.406–416
How to cite: Arnaut, M., Wöhler, C., Misra, D., Bhatt, M., and Ganesh, S.: The Moon as an Asteroid: Unlocking Surface Secrets with Atlas Polarimetry, EPSC-DPS Joint Meeting 2025, Helsinki, Finland, 7–13 Sep 2025, EPSC-DPS2025-1232, https://doi.org/10.5194/epsc-dps2025-1232, 2025.
Our study investigates the potential effects of intense solar radiation heating on the physical properties of carbonaceous asteroids, such as surface textures, particle-size distributions, and porosity. The observed number of near-Earth asteroids (NEAs) with small perihelion distances (q) is smaller than theoretically predicted (Granvik et al. 2016), indicating that NEAs are catastrophically disrupted near the Sun. One proposed destruction mechanism is that intense solar radiation induces thermal fracturing, eventually leading to breakup. Notably, (3200) Phaethon has exhibited recurrent activity near its perihelion (q = 0.14 au), such as dust and/or gas ejection over several decades (Jewitt et al. 2015), suggesting it may be experiencing thermal disruption. At this moment, the physical properties of NEA surfaces can provide insights into the mechanisms affecting them during close solar encounters.
However, the effects of solar heating on the physical properties of NEA surfaces have not been extensively studied. For example, it remains unclear whether radiation heating causes sintering (leading to enlarged particles), thermal fracturing (leading to finer particles), or whether unknown mechanisms affect the resulting particle-size distributions. To address this, we simulate the near-Sun environment in the laboratory by using the Space and High-Irradiation Near-Sun Simulator located at Luleå University of Technology’s Space Campus in Kiruna, Sweden (Tsirvoulis et al., 2022), where the carbonaceous chondrite simulants (Britt et al., 2019) are irradiated under vacuum (∼10-5 atm), using a solar-like spectrum in the visible range. We have carried out the experiments at intensity levels equivalent to those at a heliocentric distance of 0.12 au, and varied the sample characteristics such as particle sizes and compositions. We find that radiation heating alters the physical properties of the simulants. For example, tamped fine-grained samples of CM simulant (samples sieved by the 351 µm sieve) show a few hundred-micrometer-sized aggregates, pits, and millimeter-scale cracks after heating (Fig. 1).
We will present our experimental results. Then, by combining these with previous polarimetric laboratory studies, we interpret the polarimetric properties of NEAs observed at large phase angles, such as the maximum polarization degree and the maximum phase angle. For this discussion, we use polarimetric measurements from both previous studies and our own observations conducted by using ALFOSC on the Nordic Optical Telescope.
Figure 1. Stereo microscope images of (a) the tamped fine-grained samples of CM simulant before radiation heating, and (b–f) after radiation heating. White scale bars are shown at the top left of each image, with scales of 2 mm, 500 μm, 2 mm, 2 mm, 500 μm, and 500 μm for (a), (b), (c), (d), (e), and (f), respectively. Please note that image brightness and color vary due to differences in exposure time between images and are not normalized.
How to cite: Geem, J., Granvik, M., Schirner, L., Tsirvoulis, G., Toliou, A., and Fürst, P.: Investigating the Physical Properties of NEAs under Intense Solar Radiation via laboratory experiments and polarimetric observations, EPSC-DPS Joint Meeting 2025, Helsinki, Finland, 7–13 Sep 2025, EPSC-DPS2025-597, https://doi.org/10.5194/epsc-dps2025-597, 2025.
We introduce a newly developed polarimeter, the Seoul National University QUadruple Imaging Device for POLarimetry (SQUIDPOL). Polarimetry is a powerful technique in astronomy for investigating the physical properties of celestial bodies such as small Solar System objects. In the visible wavelength range, Wollaston prisms have often been used to achieve high-precision polarization measurements. However, despite their high accuracy, Wollaston prism-based polarimeters have limitations, including a narrow field of view and the need for collimating optics. SQUIDPOL employs a non-polarizing beamsplitter, four wire-grid polarizers, and four CMOS imagers (Fig. a). By using wire-grid polarizers instead of the commonly adopted Wollaston prisms, SQUIDPOL achieves a moderate field of view (15.6 × 10.7 arcmin²) with a single exposure, which is wider than that of typical Wollaston-based systems (Fig. b).
In this presentation, we share the design, development process, and performance evaluation of SQUIDPOL, currently mounted on the 60-cm telescope at the Pyeongchang Observatory of Seoul National University in South Korea. SQUIDPOL is well suited for observing small Solar System objects due to its low-altitude observation capability (down to ~10° altitude), lower competition for telescope time, and single-exposure polarimetry that minimizes the rotational effects of these bodies. SQUIDPOL aims to achieve a polarization accuracy of ΔP ~ 0.1%. This presentation includes results from laboratory experiments conducted on an optical table to validate the design, as well as performance assessments based on actual observations. We also introduce our recent scientific applications of SQUIDPOL, such as the polarimetric observation of Comet Tsuchinshan–ATLAS (C/2023 A3; Lim et al. 2025, ApJL, 983, L19). Finally, we provide practical information for potential users, including operational procedures, remote observation capabilities, and telescope usage policies.
. 
Figure (a) Optical layout of SQUIDPOL. HWP and WGF denote the half-wave plate and wire-grid filter, respectively. B1 represents the first branch, reflected by the non-polarizing beamsplitter (NPBS), while B2 is the second branch, transmitted through the NPBS.
Figure (b) A set of four images captured by SQUIDPOL in a single exposure. These images show Comet C/2023 A3, observed on 2024 October 17.
How to cite: Geem, J., Jin, S., Ishiguro, M., Park, W., Oh, H., Park, C., Lim, B., Choi, S., and Seo, J.: Design and Performance Evaluation of SQUIDPOL: A Polarimeter for Small Solar System Bodies with the SNU 60-cm Telescope, EPSC-DPS Joint Meeting 2025, Helsinki, Finland, 7–13 Sep 2025, EPSC-DPS2025-579, https://doi.org/10.5194/epsc-dps2025-579, 2025.
The wide-angle polarimetric camera (PolCam) aboard Danuri, South Korea’s first lunar orbiter, represents the first instrument to perform global polarimetric observations of the lunar surface. Since April 2023, PolCam has been conducting polarimetric observations at visible wavelengths of 430 and 750 nm for nearly two years. The mission aims to acquire at least three observation sets across a range of phase angles for latitudes between –70° and +70°. Polarimetric measurements provide critical insight into regolith grain size, a fundamental physical property of the lunar surface, thus PolCam dataset will play a crucial role in advancing our understanding of lunar surface characteristics. Because the degree of polarization on the Moon reaches its maximum near a 100° phase angle, acquiring data at high phase angles is essential; accordingly, PolCam was designed with a 45° off‑nadir tilt, facilitating observations at phase angles up to 135°. Off-nadir observations experience substantially greater geometric distortion compared to nadir measurements, rendering precise geometric calibration and inter-channel alignment imperative for accurate polarization degree estimations. Furthermore, unexpected smear artifacts were identified in all PolCam images, and addressing these effects was both essential and technically challenging to ensure reliable polarization data. In this presentation, we describe the geometric and radiometric calibration procedures necessary to derive polarimetric data and present the first-ever polarimetric measurements in lunar orbit.
For geometric calibration, we employed feature detection and matching techniques to obtain matched point pairs between PolCam and Kaguya MI images and built control networks of over 30,000 matched point pairs. Through bundle adjustment, we derived the extrinsic parameters (mounting angles on the spacecraft body) and the intrinsic parameters of each channel (focal length, principal point, and optical distortion coefficients). Incorporating these parameters into the geometric correction pipeline effectively mitigates distortions induced by complex lunar topography. Figure 1 compares the Copernicus crater before and after geometric correction: Panel (a) displays raw data from five orbital tracks, whereas Panel (b) depicts the mosaic after correction and simple cylindrical projection. The boundaries between orbital tracks are seamlessly aligned, even in highly curved regions near the crater rim, with an alignment accuracy of about 2–3 pixels.
Figure 1. Geometric correction of Copernicus crater. (a) Raw PolCam data from five contiguous orbital tracks. (b) Mosaic after geometric correction and simple cylindrical projection, showing seamless registration across track boundaries.
Radiometric calibration of PolCam includes dark current removal, flat-fielding, and smear correction. In particular, smear artifacts induced by the characteristics of the frame-transfer CCD critically impacts the accuracy of polarization measurements. Figure 2 compares a heavily smeared crater before and after smear correction: Panel (a) applies dark removal and flat-fielding only, whereas Panel (b) incorporates smear correction. Residual artifacts that caused vertical elongation of the crater have been effectively removed. Figure 3 illustrates the 430 nm intensity and degree of polarization of the Reiner Gamma swirl to demonstrate the impact of smear on polarization measurements. Panel (a) presents the results without smear correction, where the “eye-shape” structure of the swirl is not clearly resolved in the polarization image. In contrast, Panel (b) displays the results after smear correction, with enhanced contrast between bright and dark regions in the intensity image, and a pronounced depiction of the swirl’s eye-shape in the polarization image.
Figure 2. Smear correction in a heavily smeared lunar crater. (a) Images following dark-current removal and flat-fielding only, in which vertical streak artifacts produce a stretched appearance. (b) Images after additional frame-transfer smear correction, with streak artifacts effectively removed and true crater morphology restored.
Figure 3. Impact of smear on 430 nm intensity and degree of polarization of the Reiner Gamma swirl. (a) Without smear correction: intensity (left) and polarization (right) images, in which the characteristic “eye‑shape” of the swirl is obscured. (b) With smear correction: intensity (left) exhibits enhanced contrast between bright and dark regions, and the “eye‑shape” structure appears clearly in the polarization (right) image.
Over the past two years, we have operated PolCam in lunar orbit, successfully covering most lunar regions across a broad range of phase angles. Throughout this period, we continuously solved unexpected problems and encountered various trial-and-error in the calibration processes to produce reliable polarization data. In particular, substantial effort was devoted to accurately estimating the intrinsic parameters of the optical system from the observational data and to recovering polarization signals obscured by smear artifacts. Following extensive testing and refinement, we successfully generated the high-resolution polarization datasets. These data are expected to provide new insights for a wide range of studies aimed at understanding the evolution of the lunar surface.
How to cite: Baek, K., Kim, S. S., and Jeong, M.: Calibration of Danuri/Wide-Angle Polarimetric Camera (PolCam): Preliminary Results, EPSC-DPS Joint Meeting 2025, Helsinki, Finland, 7–13 Sep 2025, EPSC-DPS2025-1126, https://doi.org/10.5194/epsc-dps2025-1126, 2025.
Asteroids show significant variation in the polarisation properties of their reflected light, which are diagnostic of their surface mineralogy, geometric albedo, and texture. These properties have historically been used to characterise them; however, this remains an under-explored method for their taxonomic classification. Potentially Hazardous Asteroids (PHAs) form a particularly important sample of observable asteroids due to their potential for collision with the Earth and their near passes, which offer opportunities for close study with telescopes or intercepting spacecraft.
Using the 2-metre Liverpool Telescope (LT) and its polarimeter, MOPTOP, robotic linear polarimetry was performed for five PHAs - Didymos, 2023 BU, 2014 HK129, 2010 XC15, and 2006 BE55 - and one Near-Earth Asteroid, 2015 RN35. For three of these objects, the author is not aware of any prior polarimetric data. At least one linear polarisation measurement was made for all six asteroids; depending on the number of observations, further properties could also be determined. For the three asteroids with greater than one data point, a phase-polarisation relationship was constructed, and the geometric albedos and inversion angles were calculated. Classifying asteroids is significantly easier at high phase angles, due to the phase-polarisation curve morphology diverging significantly between classes in this region [1]. Even a single measurement at a high phase angle (>40°) hence holds significant diagnostic power. A classification was therefore deduced for all six asteroids according to the established Tholen taxonomic system [2]. Inferences were thereafter made about their chemical composition.
The polarimetric properties of the binary asteroid Didymos-Dimorphos were characterised in detail, motivated by the impact of the DART spacecraft upon Dimorphos mere weeks prior to the commencement of this study’s observations. Didymos appeared to return to its pre-DART impact polarimetric behaviour within four weeks: no detectable polarimetric signature was observed from the impact’s debris tail, suggesting the tail had dissipated to the point of being undetectable by the LT+MOPTOP. In addition to the geometric albedo and inversion angle, the magnitude and phase angle of Didymos’ polarisation minimum were estimated. Remarkably, our results are very similar to those obtained with the VLT: a telescope four times the size of the LT.
Figure 1: Coloured curves show the typical polarisation behaviour of four asteroid spectral classes commonly found among PHAs. The curves are digitised reproductions of averaged data for asteroids of low (C, F), moderate (S), and high (E) geometric albedos [2]. The dotted extensions to the curves are extrapolations beyond the low-phase angle domain in which they were observed and modelled (α ≤ 30° ); it is likely that the linear behaviour shown breaks down into a maximum at high phase angles. Blue symbols represent Didymos data taken with the LT+MOPTOP in the R band. Red symbols indicate reproduced VLT data [3], also in the R band. Empty circles show data taken prior to the impact of the NASA Double Asteroid Redirection Test spacecraft on Dimorphos, the binary partner of Didymos; crosses refer to data taken after the collision. Errorbars on these points would be of similar or smaller size to the symbols, therefore were not shown. Through visual inspection, we polarimetrically classified Didymos as an S-type asteroid .
The Liverpool Telescope and MOPTOP are shown to be ideally situated to expand the literature dataset of PHA polarimetry. The sample of objects observed in this study makes a significant contribution to the existing sample of PHAs studied with high-phase angle polarimetry. Our observation of asteroid 2023 BU was notable in several regards: it made one of the closest recorded approaches ever of an asteroid to Earth without impact (0.03 Lunar Distances), and we believe it to be one of the smallest asteroids ever to be measured with polarimetry. The variation of polarisation with wavelength was also tested via a multi-filter approach on 2015 RN35, and results suggested that the NEA may have an unusually high porosity.
References: [1] Tholen, D. J., 1984, PhD thesis, University of Arizona. [2] Belskaya, I. N. et al., 2017, Icarus, 283:30-42. [3] Bagnulo, S. et al., 2023, The Astrophysical Journal Letters, 945(2):L38.
How to cite: Wilson, R. and Wiersema, K.: Polarimetric Classification of Potentially Hazardous Asteroids with 2-m Liverpool Telescope, EPSC-DPS Joint Meeting 2025, Helsinki, Finland, 7–13 Sep 2025, EPSC-DPS2025-2083, https://doi.org/10.5194/epsc-dps2025-2083, 2025.