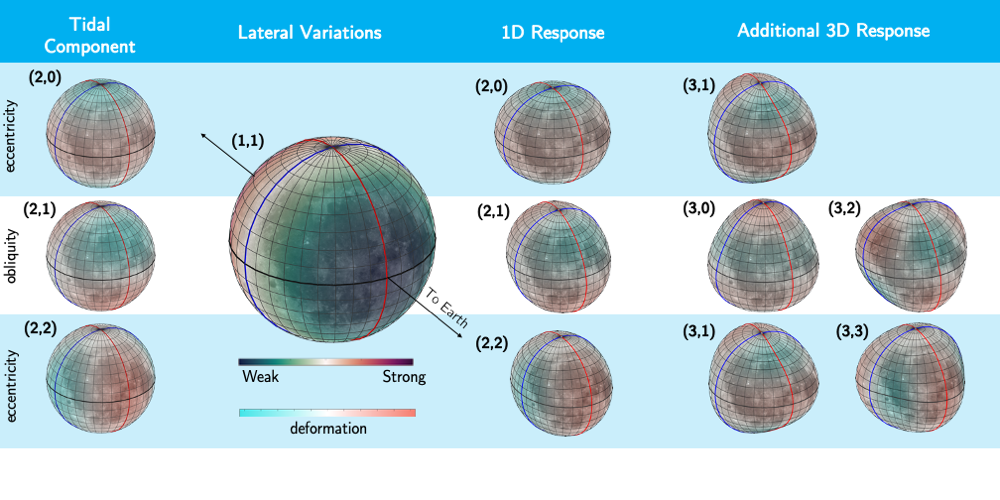
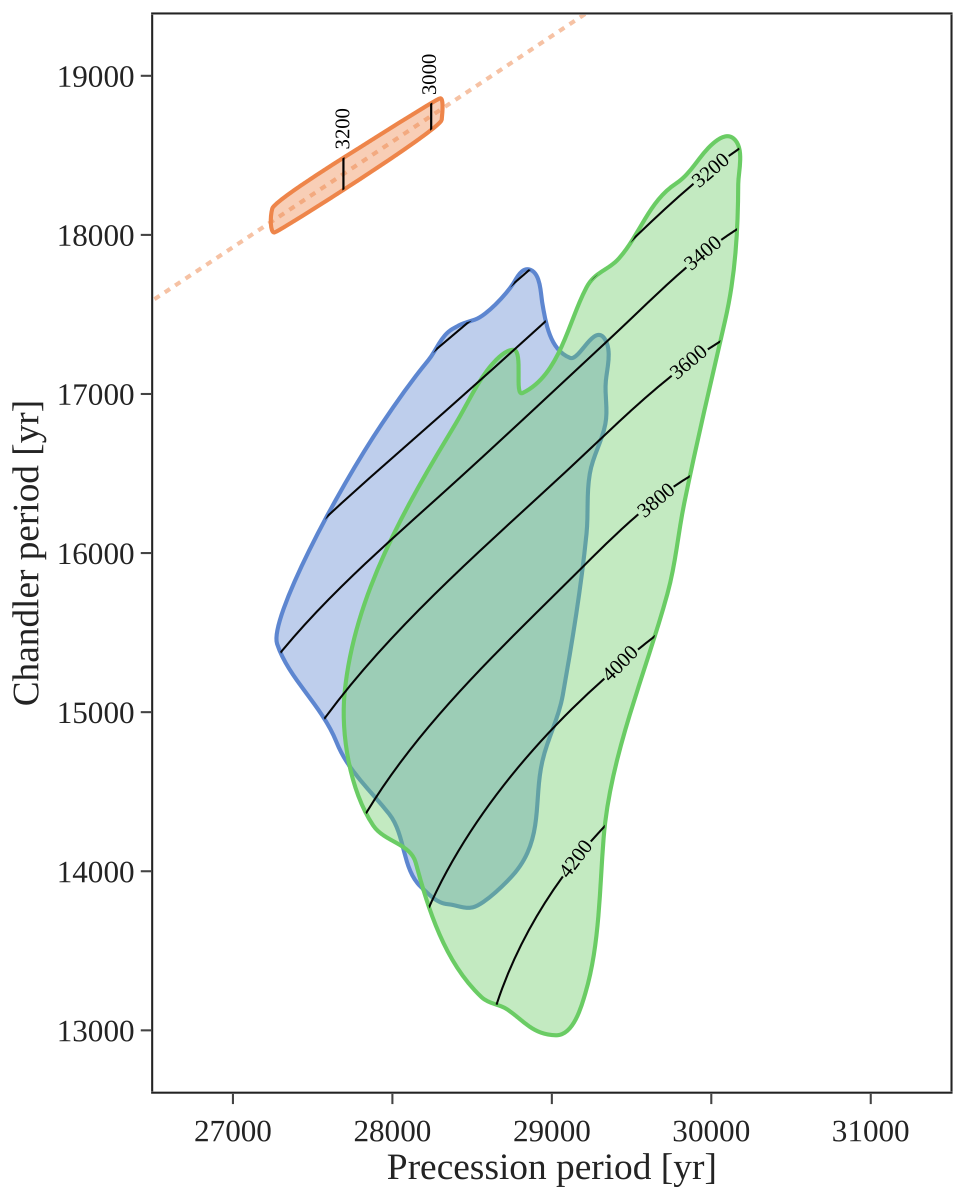
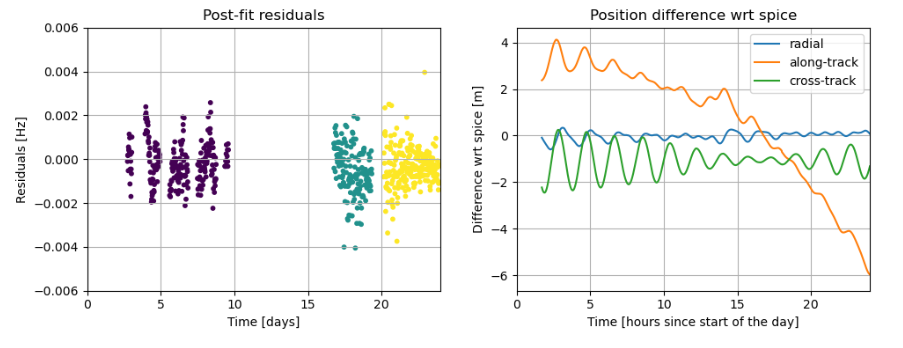
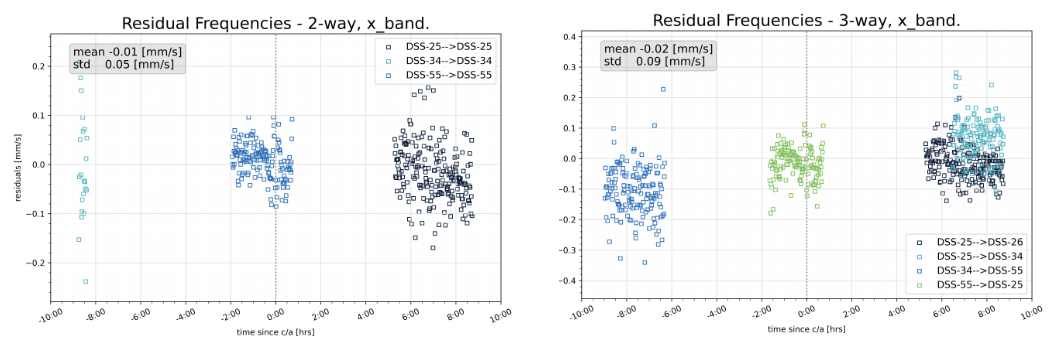
TP13
Planetary Dynamics: Shape, Gravity, Orbit, Tides, and Rotation from Observations and Models
Convener:
Haifeng Xiao
|
Co-conveners:
Attilio Rivoldini,
Alexander Berne,
Alexander Stark,
Vishnu Viswanathan,
William Desprats
Orals TUE-OB2
|
Tue, 09 Sep, 09:30–10:30 (EEST) Room Uranus (Helsinki Hall)
Posters TUE-POS
|
Attendance Tue, 09 Sep, 18:00–19:30 (EEST) | Display Tue, 09 Sep, 08:30–19:30 Finlandia Hall foyer, F53–64
Session assets
09:30–09:42
|
EPSC-DPS2025-49
|
ECP
|
On-site presentation
09:42–09:54
|
EPSC-DPS2025-1447
|
ECP
|
On-site presentation
09:54–10:06
|
EPSC-DPS2025-1617
|
ECP
|
On-site presentation
10:06–10:18
|
EPSC-DPS2025-325
|
ECP
|
On-site presentation
10:18–10:30
|
EPSC-DPS2025-1543
|
On-site presentation
F53
|
EPSC-DPS2025-1458
|
ECP
|
On-site presentation
F54
|
EPSC-DPS2025-641
|
ECP
|
On-site presentation
F55
|
EPSC-DPS2025-1702
|
ECP
|
On-site presentation
F56
|
EPSC-DPS2025-995
|
On-site presentation
F57
|
EPSC-DPS2025-1486
|
Virtual presentation
F58
|
EPSC-DPS2025-1659
|
On-site presentation
F59
|
EPSC-DPS2025-673
|
On-site presentation
F60
|
EPSC-DPS2025-1567
|
ECP
|
On-site presentation
F61
|
EPSC-DPS2025-949
|
ECP
|
On-site presentation
F62
|
EPSC-DPS2025-1215
|
ECP
|
On-site presentation
F63
|
EPSC-DPS2025-1773
|
On-site presentation
F64
|
EPSC-DPS2025-1502
|
ECP
|
On-site presentation